辽宁省鞍山市千山区2021-2022学年七年级上学期期中数学试题

试卷更新日期：2022-06-15 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各数：-4，-2.8，0， $| - 4 |$ ，其中比-3小的数是（）

A、-4 B、 $| - 4 |$ C、0 D、-2.8

查看试题解析
2. 一个矩形的周长为30，若矩形的一边长用字母x表示，则此矩形的面积为 $($ $)$

A、 $x (15 - x)$ B、 $x (30 - x)$ C、 $x (30 - 2 x)$ D、 $x (15 + x)$

查看试题解析
3. 若一个数的倒数仍是这个数，那么这个数是（）

A、0 B、1或-1 C、1 D、-1

查看试题解析
4. 下列各式变形正确的是（）

A、由 $- \frac{1}{3} x = \frac{2}{3} y$ 得 $x = 2 y$ B、由 $3 x - 2 = 2 x + 2$ 得 $x = 4$ C、由 $2 x - 3 = 3 x$ 得 $x = 3$ D、由 $3 x - 5 = 7$ 得 $3 x = 7 - 5$

查看试题解析
5. 单项式－ $\frac{2 π a^{2} b}{7}$ 的系数和次数分别是（）．

A、－ $\frac{2}{7}$ ， 3 B、－ $\frac{2}{7}$ ， 2 C、－ $\frac{2 π}{7}$ ， 2 D、－ $\frac{2 π}{7}$ ， 3

查看试题解析
6. 已知a，b，c三个有理数在数轴上对应的位置如图所示，化简：|a+c|﹣|b﹣c|+|b|的值为（）

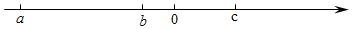A、﹣2b﹣a B、﹣2b+a C、2c+a D、﹣2c﹣a

查看试题解析
7. 若 $- 3 x^{2 m} y^{3}$ 与 $2 x^{4} y^{n}$ 是同类项，则 $| m - n |$ 的值是（）．

A、0 B、1 C、7 D、-1

查看试题解析
8. 人民日报记者从工信部获悉，今年前三季度，我国信息通信业运行总体平稳．新建光缆线路329万千米，光缆线路总长度达到4646万千米，同比增长12.5%．请将新建光缆线路长度用科学记数法表示为（）

A、46.46×10⁶千米 B、4.646×10⁷千米 C、0.329×10⁷千米 D、3.29×10⁶千米

查看试题解析
9. 两件商品都卖84元，其中一件亏本20%，另一件赢利40%，则两件商品卖后（）

A、赢利16.8元 B、亏本3元 C、赢利3元 D、不赢不亏

查看试题解析
10. 如图，将 $- 3 ， - 2 ， - 1 ， 0 ， 1 ， 2 ， 3 ， 4 ， 5$ 分别填人九个空格内，使每行、每列、每条对角线上的三个数之和相等，现在 $a ， b ， c$ 分别表示其中的一个数，则 $a - b + c$ 的值为（）

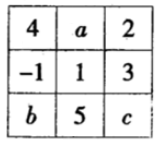A、-5 B、-4 C、0 D、5

查看试题解析

二、填空题

11. 比较大小： $- \frac{1}{2}$ $- \frac{1}{3}$ （小“＞“，“＜”或“＝“）．

查看试题解析
12. 已知|a+1|=0，b²=9，则a+b= ．

查看试题解析
13. 某轮船顺水航行 3h，逆水航行 1.5h，已知轮船在静水中的速度为 a km/h，水流速度是 y km/h，则轮船共航行km.

查看试题解析
14. 近似数 $2.30 \times 1 0^{4}$ 的精确度是．

查看试题解析
15. 若关于a，b的多项式 $3 (a^{2} - 2 a b - b^{2}) - (a^{2} + m a b + 2 b^{2})$ 中不含有ab项，则 $m =$ ．

查看试题解析
16. 若关于 $x$ 的方程 $(2 a + 1) x^{2} + 5 x^{b - 2} - 7 = 0$ 是一元一次方程，则方程 $a x + b = 0$ 的解是．

查看试题解析
17. 已知x﹣2y=﹣2，则3+2x﹣4y= ．

查看试题解析
18. 定义“*”的运算规则为 $a * b = a + 2 b$ ，若 $(3 * x) + (x * 3) = 12$ ，则 $x$ 的值是．

查看试题解析

三、解答题

19. 计算：

(1)、 $- 7^{2} + 2 \times (- 3)^{2} + (- 6) \div {(- \frac{1}{3})}^{2}$ ；

(2)、用简便方法计算： $- 99 \frac{15}{17} \times 34$ ．

查看试题解析
20. 小明练习跳绳．以1分钟跳165个为目标，并把20次1分钟跳绳的数量记录如表（超过165个的部分记为“ $+$ ”，少于165个的部分记为“ $-$ ”）
与目标数量的差异（单位：个）
-11
-6
-2
+4
+10
次数
4
5
3
6
2

(1)、小明在这20次跳绳练习中，1分钟跳绳个数最多的一次比最少的一次多几个？

(2)、小明在这20次跳绳练习中，累计跳绳多少个？

查看试题解析
21. 解方程： $2 (x - 2) - 6 (x - 1) = 3 (1 - x)$

查看试题解析
22. 已知代数式 $A = 3 x - x + 1$ ，马小虎同学在做整式加减运算时，误将“ $A - B$ ”看成“ $A + B$ ”了，计算结果是 $2 x - 3 x - 2$ ．

(1)、请你帮马小虎同学求出正确的结果；

(2)、若x是最大的负整数，则将x的值代入第（1）问的结果求得的值为．

查看试题解析
23. 为了迎接学校艺术节的召开，现要从七、八年级学生中抽调a人参加“校园集体舞”、“广播体操”、“唱红歌”等训练活动，其中参加“校园集体舞”人数是抽调人数的 $\frac{1}{4}$ 还多3人，参加“广播体操”活动人数是抽调人数的 $\frac{1}{2}$ 少2人，其余的参加“唱红歌”活动，若抽调的每个学生只参加了一项活动．

(1)、求参加“唱红歌”活动的人数．(用含a的式子表示)

(2)、求参加“广播体操”比参加“校园集体舞蹈”多的人数．(用含a的式子表示)

(3)、求当a=84时，参加“广播体操比赛”的人数．

查看试题解析
24. 观察下列各式，回答问题．
$1 - \frac{1}{2^{2}} = \frac{1}{2} \times \frac{3}{2}$ ，
$1 - \frac{1}{3^{2}} = \frac{2}{3} \times \frac{4}{3}$ ，
$1 - \frac{1}{4^{2}} = \frac{3}{4} \times \frac{5}{4}$ …
按上述规律填空：

(1)、 $1 - \frac{1}{10 0^{2}} =$ × ．

(2)、计算： $(1 - \frac{1}{2^{2}}) \times (1 - \frac{1}{3^{2}}) \times \cdot \cdot \cdot \times (1 - \frac{1}{202 0^{2}}) \times (1 - \frac{1}{202 1^{2}})$ ．

查看试题解析
25. 《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等，交易其一，金轻十六两，问金、银一枚各重几何？”意思是：甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相等，两袋互相交换1枚后，甲袋比乙袋轻了16两（袋子重量忽略不计），问黄金、白银每枚各重多少两？

查看试题解析

与目标数量的差异（单位：个）	-11	-6	-2	+4	+10
次数	4	5	3	6	2