河北省邢台市信都区2021-2022学年七年级上学期期中数学试题
试卷更新日期:2022-06-15 类型:期中考试
一、单选题
-
1. 下列各图中,表示“射线 ”的中( )A、
 B、
B、 C、
C、 D、
D、 2. 有如下两个问题:①7和﹣7是一对相反数;②﹣7和﹣是一对倒数,则有( )A、①正确,②错误 B、①、②均正确 C、①错误,②正确 D、①、②均错误3. 检测4袋茶叶的质量,超过标准的克数记为正数,不足的克数记为负数,从重量的角度来看,最接近标准的那一袋是( )A、+3 B、-0.3 C、+0.2 D、-3.64. 围成下列这些立体图形的各个面中,都是平的面为( )A、
2. 有如下两个问题:①7和﹣7是一对相反数;②﹣7和﹣是一对倒数,则有( )A、①正确,②错误 B、①、②均正确 C、①错误,②正确 D、①、②均错误3. 检测4袋茶叶的质量,超过标准的克数记为正数,不足的克数记为负数,从重量的角度来看,最接近标准的那一袋是( )A、+3 B、-0.3 C、+0.2 D、-3.64. 围成下列这些立体图形的各个面中,都是平的面为( )A、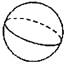 B、
B、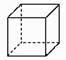 C、
C、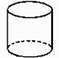 D、
D、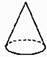 5. 如图,在应用有理数减法法则,进行运算时,下列说法正确的是( )
5. 如图,在应用有理数减法法则,进行运算时,下列说法正确的是( )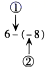 A、①、②均需变成“+” B、只有①变成“+” C、只有①变成“×” D、只有②变成“+”6. 若6□(﹣3)=﹣2,则□表示的运算符号是( )A、+ B、﹣ C、× D、÷7. 如图,将甲,乙两把尺子拼在一起,两端重合,如果甲尺经校定是直的,那么乙尺不是直的,判断依据是( )
A、①、②均需变成“+” B、只有①变成“+” C、只有①变成“×” D、只有②变成“+”6. 若6□(﹣3)=﹣2,则□表示的运算符号是( )A、+ B、﹣ C、× D、÷7. 如图,将甲,乙两把尺子拼在一起,两端重合,如果甲尺经校定是直的,那么乙尺不是直的,判断依据是( )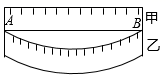 A、两点之间直线最短 B、经过一点有且只有一条直线 C、经过两点有且只有一条直线 D、线段可以向两个方向延长8. 在下列执行异号两数相加的步骤中,错误的是( )
A、两点之间直线最短 B、经过一点有且只有一条直线 C、经过两点有且只有一条直线 D、线段可以向两个方向延长8. 在下列执行异号两数相加的步骤中,错误的是( )①求两个有理数的绝对值;②比较两个有理数绝对值的大小;③将两个有理数绝对值的和作为结果的绝对值;④将绝对值较大数的符号作为结果的符号.
A、① B、② C、③ D、④9. 如图,在数轴上,注明了四段的范围,若某段上有两个整数,则这段是( )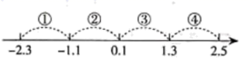 A、段① B、段② C、段③ D、段④10. 若a表示正整数,且﹣<﹣ , 则a的值可以是( )A、1 B、3 C、5 D、711. 若两个图形有公共点,则称这两个图形相交,否则称它们不相交.如图,直线PA、PB和线段AB将平面分成五个区域(不包含边界),若线段PQ与线段AB相交,则点Q落在的区域是( )
A、段① B、段② C、段③ D、段④10. 若a表示正整数,且﹣<﹣ , 则a的值可以是( )A、1 B、3 C、5 D、711. 若两个图形有公共点,则称这两个图形相交,否则称它们不相交.如图,直线PA、PB和线段AB将平面分成五个区域(不包含边界),若线段PQ与线段AB相交,则点Q落在的区域是( )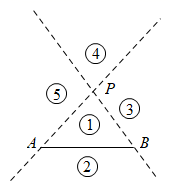 A、① B、② C、③ D、④或⑤12. 为计算简便,把(﹣2.4)﹣(﹣4.7)﹣(+0.5)+(﹣3.5)写成省略加号的和的形式,正确的是( )A、﹣2.4﹣4.7﹣0.5﹣3.5 B、﹣2.4+4.7+0.5﹣3.5 C、﹣2.4+4.7﹣0.5﹣3.5 D、﹣2.4+4.7﹣0.5+3.513. 计算:72°22′+50°40′30″的结果是( )A、122°62′30″ B、123°2′30″ C、122°2′30″ D、123°12′30″14. 嘉淇在用直尺和圆规作一个角等于已知角的步骤如下:
A、① B、② C、③ D、④或⑤12. 为计算简便,把(﹣2.4)﹣(﹣4.7)﹣(+0.5)+(﹣3.5)写成省略加号的和的形式,正确的是( )A、﹣2.4﹣4.7﹣0.5﹣3.5 B、﹣2.4+4.7+0.5﹣3.5 C、﹣2.4+4.7﹣0.5﹣3.5 D、﹣2.4+4.7﹣0.5+3.513. 计算:72°22′+50°40′30″的结果是( )A、122°62′30″ B、123°2′30″ C、122°2′30″ D、123°12′30″14. 嘉淇在用直尺和圆规作一个角等于已知角的步骤如下:已知:∠AOB
求作:∠A′O′B′,使∠A′O′B′=∠AOB
作法:⑴如图,以点O为圆心,m为半径画弧,分别交OA,OB于点C,D;
⑵画一条射线O′A′,以点O′为圆心,n为半径画弧,交O′A′于点C′;
⑶以点C′为圆心,p为半径画弧,与第(2)步中所画的弧相交于点D′;
⑷过点D′画射线O′B′,则∠A′O′B′=∠AOB.
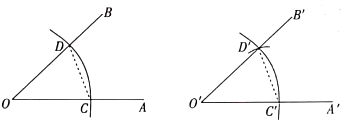
下列说法正确的是( )
A、m=p>0 B、n=p>0 C、p=n>0 D、m=n>0二、填空题
-
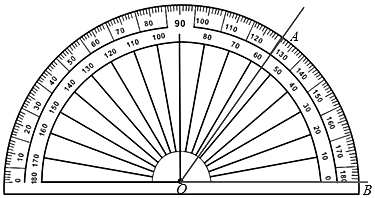
15. 如图所示,用量角器度量∠AOB,可以读出∠AOB的度数为 , ∠AOB的余角的度数为 .
 16. 在计算这一变形依据了 , 此题的计算结果是 .17. 如图,线段AB上的点数与线段的总数有如下关系:如果线段AB上有三个点时,线段总共有=3条,如果线段AB上有4个点时,线段总数有=6条,如果线段AB上有5个点时,线段总数共有=10条,……
16. 在计算这一变形依据了 , 此题的计算结果是 .17. 如图,线段AB上的点数与线段的总数有如下关系:如果线段AB上有三个点时,线段总共有=3条,如果线段AB上有4个点时,线段总数有=6条,如果线段AB上有5个点时,线段总数共有=10条,……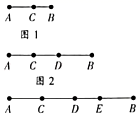 (1)、当线段AB上有6个点时,线段总数共有条;(2)、某学校七年级共有10个班进行辩论赛,规定进行单循环赛(每两班赛一场),那么该校七年级的辩论赛的场数是 .
(1)、当线段AB上有6个点时,线段总数共有条;(2)、某学校七年级共有10个班进行辩论赛,规定进行单循环赛(每两班赛一场),那么该校七年级的辩论赛的场数是 .三、解答题
-
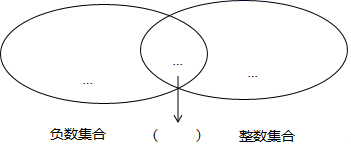
18. 把下面一组数填入图中相应的位置,并填写公共部分的名称.0.7,﹣10,+3.4,﹣4 , 0,85,0.4
 19. 如图,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点.
19. 如图,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点.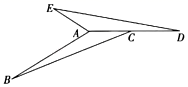 (1)、指出旋转中心.(2)、若∠BAE=60°,求出旋转角的度数.(3)、若AB=4,求AE的长.20. 老师设计了接力游戏,用合作的方式完成有理数运算,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简.过程如图所示:
(1)、指出旋转中心.(2)、若∠BAE=60°,求出旋转角的度数.(3)、若AB=4,求AE的长.20. 老师设计了接力游戏,用合作的方式完成有理数运算,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简.过程如图所示: (1)、接力中,计算错误的学生是;(2)、请给出正确的计算过程.21. 如图,已知点A、B、C、D、E在同一直线上,且AC=BD,E是线段BC的中点.
(1)、接力中,计算错误的学生是;(2)、请给出正确的计算过程.21. 如图,已知点A、B、C、D、E在同一直线上,且AC=BD,E是线段BC的中点.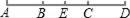 (1)、点E是线段AD的中点吗?说明理由;(2)、当AD=10,AB=3时,求线段BE的长度.22. 某仓库在一周的货品运输中,进出情况如表(进库为正,出库为负,单位:吨):
(1)、点E是线段AD的中点吗?说明理由;(2)、当AD=10,AB=3时,求线段BE的长度.22. 某仓库在一周的货品运输中,进出情况如表(进库为正,出库为负,单位:吨):星期一
星期二
星期三
星期四
星期五
星期六
星期天
合计
+26
﹣16
+42
﹣30

﹣25
﹣9
+6
表中星期五的进出数被墨水涂污了.
(1)、请你算出星期五的进出数;(2)、如果进出的装卸费都是每吨10元,那么这一周要付多少元装卸费?23. 如图,小明将两块完全相同的直角三角形纸片的直角顶点C叠放在一起,若保持△BCD不动,将△ACE绕直角顶点C旋转.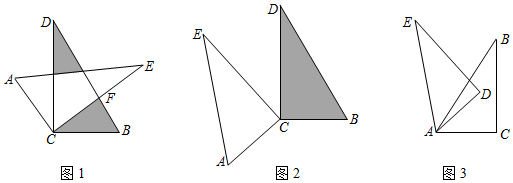 (1)、论证:如图1,如果CD平分∠ACE,说明CE平分∠BCD.(2)、发现:如图1,若∠DCE=35°,则∠ACB=°;若∠ACB=140°,则∠DCE=°;(3)、总结:当直角三角形ACE纸片绕直角顶点C旋转到如图1的位置时,猜想∠ACB与∠DCE的数量关系为 ▲ ;当△ACE绕直角顶点C旋转到如图2的位置时,上述关系是否依然成立,请说明理由;(4)、拓展:在图3中, 将直角三角形ADE纸片绕顶点A逆时针旋转40°角到如图的位置 , 已知∠CAE=100°,直接写出∠BAD的度数.24. 我国著名数学家华罗庚说过“数缺形时少直观,形少数时难人微”,数形结合是解决数学问题的重要思想方法.请阅读下列材料:
(1)、论证:如图1,如果CD平分∠ACE,说明CE平分∠BCD.(2)、发现:如图1,若∠DCE=35°,则∠ACB=°;若∠ACB=140°,则∠DCE=°;(3)、总结:当直角三角形ACE纸片绕直角顶点C旋转到如图1的位置时,猜想∠ACB与∠DCE的数量关系为 ▲ ;当△ACE绕直角顶点C旋转到如图2的位置时,上述关系是否依然成立,请说明理由;(4)、拓展:在图3中, 将直角三角形ADE纸片绕顶点A逆时针旋转40°角到如图的位置 , 已知∠CAE=100°,直接写出∠BAD的度数.24. 我国著名数学家华罗庚说过“数缺形时少直观,形少数时难人微”,数形结合是解决数学问题的重要思想方法.请阅读下列材料:材料(一):代数式|x﹣2|的几何意义是数轴上表示有理数x所对应的点与表示有理数2所对应的点之间的距离;因为|x+1|=|x﹣(﹣1)|,所以|x+1|的几何意义就是数轴上表示有理数x所对应的点与表示有理数﹣1所对应的点之间的距离.
材料(二):如图,点A、B、P分别表示有理数数﹣1、2、x,AB=3,
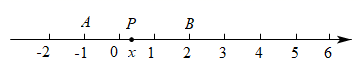
∵|x+1|+|x﹣2|的几何意义是线段PA与PB的长度之和,∴当点P在线段AB上时,PA+PB=3,当点P在点A的左侧或点B的右侧时,PA+PB>3,
∴|x+1|+|x﹣2|的最小值是3;
解决问题:
(1)、在数轴上,若点M表示的数为﹣2,点Q表示的数为1,点N表示的数为6,请画出一条数轴,标出点M、Q、N的位置,①线段NQ= ▲ ;
②若数轴上点C表示的有理数为x,求|x+2|+|x﹣6|的最小值.
(2)、若代数式|x+a|+|x﹣3|的最小值是2,求a的值.