河北省唐山市遵化市2021-2022学年七年级上学期期中数学试题
试卷更新日期:2022-06-15 类型:期中考试
一、单选题
-
1. 小戴同学的微信钱包账单如图所示,+5.20表示收入5.20元,下列说法正确的是( )
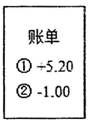 A、-1.00表示收入1.00元 B、-1.00表示支出1.00元 C、-1.00表示支出-1.00元 D、收支总和为6.20元2. 下列运算正确的是( ) .A、 B、 C、 D、3. 下列各组数中,数值相等的是( )A、34和43 B、-42和(-4)2 C、-23和(-2)3 D、(-2×3)2和-22× 324. 下列图形属于棱柱的有( )
A、-1.00表示收入1.00元 B、-1.00表示支出1.00元 C、-1.00表示支出-1.00元 D、收支总和为6.20元2. 下列运算正确的是( ) .A、 B、 C、 D、3. 下列各组数中,数值相等的是( )A、34和43 B、-42和(-4)2 C、-23和(-2)3 D、(-2×3)2和-22× 324. 下列图形属于棱柱的有( )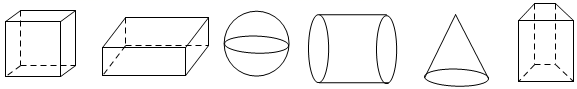 A、2个 B、3个 C、4个 D、5个5. 如果线段AB=5cm,BC=3cm,那么A、C两点间的距离是( )A、8cm B、2cm C、4cm D、不能确定6. 若α=29°45′,则α的余角等于( )A、60°55′ B、60°15′ C、150°55′ D、150°15′7. 若∠A=130°,∠B=50°,则下列说法中错误的是( )A、∠A与∠B互补. B、∠B比∠A小80°. C、∠A与∠B互余. D、∠A是钝角,∠B是锐角.8. 如图,若∠1=50°,则∠2的度数为( )
A、2个 B、3个 C、4个 D、5个5. 如果线段AB=5cm,BC=3cm,那么A、C两点间的距离是( )A、8cm B、2cm C、4cm D、不能确定6. 若α=29°45′,则α的余角等于( )A、60°55′ B、60°15′ C、150°55′ D、150°15′7. 若∠A=130°,∠B=50°,则下列说法中错误的是( )A、∠A与∠B互补. B、∠B比∠A小80°. C、∠A与∠B互余. D、∠A是钝角,∠B是锐角.8. 如图,若∠1=50°,则∠2的度数为( )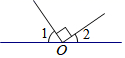 A、30° B、40° C、50° D、90°9. 下列计算正确的是( )A、﹣0.15÷3=﹣0.5 B、0.2÷0.1=0.2 C、 D、10. 下列结论正确的是( )A、一个数的绝对值一定是正数 B、任何正数一定大于它的倒数 C、− a 一定是负数 D、零与任何数相乘,乘积一定为011. 将 绕点O旋转 得到 ,则下列作图正确的是( )A、
A、30° B、40° C、50° D、90°9. 下列计算正确的是( )A、﹣0.15÷3=﹣0.5 B、0.2÷0.1=0.2 C、 D、10. 下列结论正确的是( )A、一个数的绝对值一定是正数 B、任何正数一定大于它的倒数 C、− a 一定是负数 D、零与任何数相乘,乘积一定为011. 将 绕点O旋转 得到 ,则下列作图正确的是( )A、 B、
B、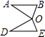 C、
C、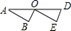 D、
D、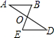 12. 曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好地观赏风光。如图, 两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是( )
12. 曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好地观赏风光。如图, 两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是( ) A、两点之间,线段最短 B、平行于同一条直线的两条直线平行 C、垂线段最短 D、两点确定一条直线13. 在﹣3,﹣2,1,4中,绝对值最小的数是( )A、4 B、﹣3 C、﹣2 D、114. 下图中能用表示的是( )A、
A、两点之间,线段最短 B、平行于同一条直线的两条直线平行 C、垂线段最短 D、两点确定一条直线13. 在﹣3,﹣2,1,4中,绝对值最小的数是( )A、4 B、﹣3 C、﹣2 D、114. 下图中能用表示的是( )A、 B、
B、 C、
C、 D、
D、 15. 如图,数轴上被墨水遮盖的数可能为( )
15. 如图,数轴上被墨水遮盖的数可能为( )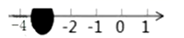 A、-1 B、-1.5 C、-3 D、-4.216. 如图,按大拇指,食指,中指,无名指,小指,无名指,中指,…的顺序从1开始数数,当数到2020时,对应的手指是( )
A、-1 B、-1.5 C、-3 D、-4.216. 如图,按大拇指,食指,中指,无名指,小指,无名指,中指,…的顺序从1开始数数,当数到2020时,对应的手指是( ) A、食指 B、中指 C、无名指 D、小指
A、食指 B、中指 C、无名指 D、小指二、填空题
-
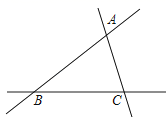
17. 若∠α=6.6°,∠β=6°6′,则∠α∠β(填:“>”,“<”或“=”).18. 直线AB,BC,CA的位置关系如图所示,则下列语句:①点A在直线BC上;②直线AB经过点C;③直线AB,BC,CA两两相交;④点B是直线AB,BC,CA的公共点,正确的有(只填写序号).
 19. 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为 .
19. 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为 .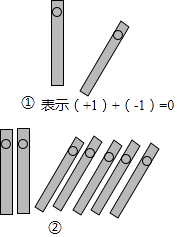
三、解答题
-
20. 某检修车从文化宫出发,在东西走向的长江路上检修线路.如果规定向东行驶为正,向西行驶为负,那么一天中八次行驶记录如下(单位:km):
+6,﹣3,+10,﹣8,+2,﹣7,﹣10,﹣4.
(1)、请你通过计算说明检修车最后是否回到文化宫;(2)、若耗油量为0.4L/km,则这一天中该检修车共耗油多少升?21. 在如图所示的一张零件图中,已知AD=73mm,BD=69mm,CD=17mm,求AB和BC的长.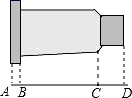 22. 现在定义两种运算“*”和“☆”,对于有理数a,b,有a*b=a+2b﹣1,a☆b=2ab+1.(1)、求5*(﹣2);(2)、求(2*3)☆(3☆2).23. 已知∠α=76°42',∠β=41°41'.
22. 现在定义两种运算“*”和“☆”,对于有理数a,b,有a*b=a+2b﹣1,a☆b=2ab+1.(1)、求5*(﹣2);(2)、求(2*3)☆(3☆2).23. 已知∠α=76°42',∠β=41°41'.求:
(1)、∠β的余角;(2)、∠α与∠β的2倍的和.24. 计算(1)、(2)、25. 如图,将一张长方形纸片按如图方式折叠,猜想折痕EF,EG的位置关系,并说明理由.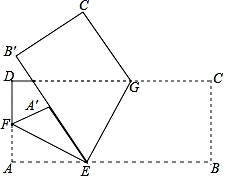 26. 如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a、c满足|a+2|+(c﹣7)2=0.
26. 如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a、c满足|a+2|+(c﹣7)2=0. (1)、a= , b= , c=;(2)、若将数轴折叠,使得A点与C点重合,则点B与数表示的点重合;(3)、点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,那么3BC﹣2AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
(1)、a= , b= , c=;(2)、若将数轴折叠,使得A点与C点重合,则点B与数表示的点重合;(3)、点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,那么3BC﹣2AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.