四川省自贡市2022年中考数学试卷
试卷更新日期:2022-06-15 类型:中考真卷
一、选择题(共12个小题,每小题4分,共48分)
-
1. 如图,直线 相交于点 ;若 ,则 的度数是( )
 A、30° B、40° C、60° D、150°2. 自贡市江姐故里红色教育基地自去年底开放以来,截止今年5月,共接待游客180000余人;人数180000用科学记数法表示为( )A、 B、 C、 D、3. 如图,将矩形纸片ABCD 绕边CD所在的直线旋转一周,得到的立体图形是( )
A、30° B、40° C、60° D、150°2. 自贡市江姐故里红色教育基地自去年底开放以来,截止今年5月,共接待游客180000余人;人数180000用科学记数法表示为( )A、 B、 C、 D、3. 如图,将矩形纸片ABCD 绕边CD所在的直线旋转一周,得到的立体图形是( )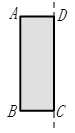 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,菱形 ABCD 对角线交点与坐标原点 O 重合,点 A(-2,5) ,则点C的坐标为( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,菱形 ABCD 对角线交点与坐标原点 O 重合,点 A(-2,5) ,则点C的坐标为( )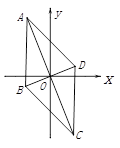 A、 B、 C、 D、6. 剪纸与扎染、龚扇被称为自贡小三绝,以下学生剪纸作品中,轴对称图形是( )A、 ,
A、 B、 C、 D、6. 剪纸与扎染、龚扇被称为自贡小三绝,以下学生剪纸作品中,轴对称图形是( )A、 , B、
B、 C、
C、 D、
D、 7. 如图,四边形 内接于⊙ , 为⊙ 的直径, ,则 的度数是( )
7. 如图,四边形 内接于⊙ , 为⊙ 的直径, ,则 的度数是( )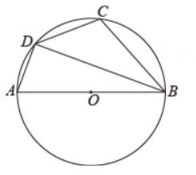 A、90° B、100° C、110° D、120°8. 六位同学的年龄分别是13、14、15、14、14、15岁,关于这组数据,正确说法是( )A、平均数是14 B、中位数是14.5 C、方差3 D、众数是149. 等腰三角形顶角度数比一个底角度数的2倍多20°,则这个底角的度数为( )A、30° B、40° C、50° D、60°10. 为⊙ 外一点, 与⊙ 相切于点 , , ,则 的长为( )A、 B、5 C、8 D、911. 九年级2班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形,等腰三角形(底边靠墙),半圆形这三种方案,最佳方案是( )
A、90° B、100° C、110° D、120°8. 六位同学的年龄分别是13、14、15、14、14、15岁,关于这组数据,正确说法是( )A、平均数是14 B、中位数是14.5 C、方差3 D、众数是149. 等腰三角形顶角度数比一个底角度数的2倍多20°,则这个底角的度数为( )A、30° B、40° C、50° D、60°10. 为⊙ 外一点, 与⊙ 相切于点 , , ,则 的长为( )A、 B、5 C、8 D、911. 九年级2班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形,等腰三角形(底边靠墙),半圆形这三种方案,最佳方案是( )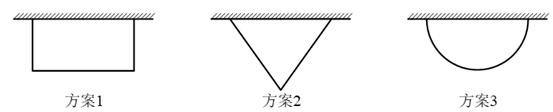 A、方案1 B、方案2 C、方案3 D、方案1或方案212. 已知 ,抛物线 顶点在线段 上运动,形状保持不变,与 轴交于 两点( 在 的右侧),下列结论:
A、方案1 B、方案2 C、方案3 D、方案1或方案212. 已知 ,抛物线 顶点在线段 上运动,形状保持不变,与 轴交于 两点( 在 的右侧),下列结论:①. ;②.当 时,一定有 随 的增大而增大;③.若点 横坐标的最小值为-5,点 横坐标的最大值为3;④.当四边形 为平行四边形时, .
其中正确的是( )
A、①③ B、②③ C、①④ D、①③④二、填空题(共6个小题,每小题4分,共24分)
-
13. 计算: .14. 分解因式: .15. 化简: = .16. 为了比较甲、乙两鱼池中的鱼苗数目,小明从两鱼池中各捞出100条鱼苗,每条做好记号,然后放回原鱼池;一段时间后,在同样的地方,小明再从甲、乙两鱼池中各捞出100条鱼苗,发现其中有记号的鱼苗分别是5条、10条,可以初步估计鱼苗数目较多的是 鱼池(填甲或乙)17. 一块圆形玻璃镜面碎成了几块,其中一块如图所示,测得弦 长20厘米,弓形高 为2厘米,则镜面半径为 厘米.
 18. 如图,矩形 中, , 是 的中点,线段 在边 上左右滑动;若 ,则 的最小值为 .
18. 如图,矩形 中, , 是 的中点,线段 在边 上左右滑动;若 ,则 的最小值为 .
三、解答题(共8个题,共78分)
-
19. 解不等式组: ,并在数轴上表示其解集.
 20. 如图,△ 是等边三角形, 在直线 上, .
20. 如图,△ 是等边三角形, 在直线 上, .

求证: .
21. 学校师生去距学校45千米的吴玉章故居开展研学活动,骑行爱好者张老师骑自行车先行2小时后,其余师生乘汽车出发,结果同时到达;已知汽车速度是自行车速度的3倍,求张老师骑车的速度.22. 为了解学生每周参加课外兴趣小组活动的累计时间 (单位:小时),学校采用随机抽样的方法,对部分学生进行了问卷调查,调查结果按 , , , 分为四个等级,分别用A、B、C、D表示;下图是受损的调查统计图,请根据图上残存信息解决以下问题:
 (1)、求参与问卷调查的学生人数 ,并将条形统计图补充完整;(2)、全校共有学生2000人,试估计学校每周参加课外兴趣小组活动累计时间不少于4小时的学生人数;(3)、某小组有4名同学,A、D等级各2人,从中任选2人向老师汇报兴趣活动情况,请用画树状图或列表法求这2人均属D等级的概率.23. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于 两点.
(1)、求参与问卷调查的学生人数 ,并将条形统计图补充完整;(2)、全校共有学生2000人,试估计学校每周参加课外兴趣小组活动累计时间不少于4小时的学生人数;(3)、某小组有4名同学,A、D等级各2人,从中任选2人向老师汇报兴趣活动情况,请用画树状图或列表法求这2人均属D等级的概率.23. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于 两点.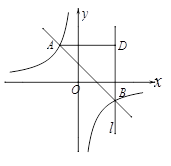 (1)、求反比例函数和一次函数的解析式;(2)、过点 作直线 ∥ 轴,过点 作直线 于 ,点 是直线 上一动点,若 ,求点 的坐标.24. 如图,用四根木条钉成矩形框 ,把边 固定在地面上,向右推动矩形框,矩形框的形状会发生改变(四边形具有不稳定性).
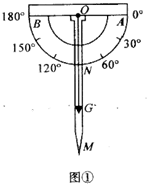
(1)、求反比例函数和一次函数的解析式;(2)、过点 作直线 ∥ 轴,过点 作直线 于 ,点 是直线 上一动点,若 ,求点 的坐标.24. 如图,用四根木条钉成矩形框 ,把边 固定在地面上,向右推动矩形框,矩形框的形状会发生改变(四边形具有不稳定性).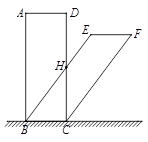 (1)、通过观察分析,我们发现图中线段存在等量关系,如线段 由 旋转得到,所以 .我们还可以得到 = , = ;(2)、进一步观察,我们还会发现 ∥ ,请证明这一结论;(3)、已知 ,若 恰好经过原矩形 边的中点 ,求 与 之间的距离.25. 某数学兴趣小组自制测角仪到公园进行实地测量,活动过程如下:(1)、探究原理制作测角仪时,将细线一段固定在量角器圆心 处,另一端系小重物 .测量时,使支杆 、量角器90°刻度线 与铅垂线 相互重合(如图①),绕点 转动量角器,使观测目标 与直径两端点 共线(如图②),此目标 的仰角 .请说明两个角相等的理由.
(1)、通过观察分析,我们发现图中线段存在等量关系,如线段 由 旋转得到,所以 .我们还可以得到 = , = ;(2)、进一步观察,我们还会发现 ∥ ,请证明这一结论;(3)、已知 ,若 恰好经过原矩形 边的中点 ,求 与 之间的距离.25. 某数学兴趣小组自制测角仪到公园进行实地测量,活动过程如下:(1)、探究原理制作测角仪时,将细线一段固定在量角器圆心 处,另一端系小重物 .测量时,使支杆 、量角器90°刻度线 与铅垂线 相互重合(如图①),绕点 转动量角器,使观测目标 与直径两端点 共线(如图②),此目标 的仰角 .请说明两个角相等的理由.
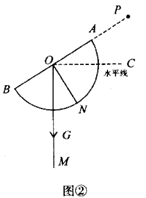 (2)、实地测量
(2)、实地测量如图③,公园广场上有一棵树,为了测量树高,同学们在观测点 处测得顶端 的仰角 ,观测点与树的距离 为5米,点 到地面的距离 为1.5米;求树高 . ( ,结果精确到0.1米)
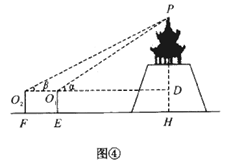
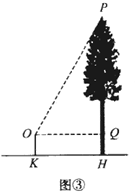 (3)、拓展探究
(3)、拓展探究公园高台上有一凉亭,为测量凉亭顶端 距离地面高度 (如图④),同学们讨论,决定先在水平地面上选取观测点 ( 在同一直线上),分别测得点 的仰角 ,再测得 间的距离 ,点 到地面的距离 均为1.5米;求 (用 表示).
 26. 已知二次函数 .
26. 已知二次函数 . (1)、若 ,且函数图象经过 , 两点,求此二次函数的解析式,直接写出抛物线与 轴交点及顶点的坐标;(2)、在图①中画出⑴中函数的大致图象,并根据图象写出函数值 时自变量 的取值范围;(3)、若 且 ,一元二次方程 两根之差等于 ,函数 图象经过 两点,试比较 的大小 .
(1)、若 ,且函数图象经过 , 两点,求此二次函数的解析式,直接写出抛物线与 轴交点及顶点的坐标;(2)、在图①中画出⑴中函数的大致图象,并根据图象写出函数值 时自变量 的取值范围;(3)、若 且 ,一元二次方程 两根之差等于 ,函数 图象经过 两点,试比较 的大小 .