浙江省丽水市2021-2022学年七年级下学期数学教学质量监测模拟卷（一）

试卷更新日期：2022-06-14 类型：期末考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分，请选出各题中一个符合题意的正确选项，不选、多选、错选均不得分）

1. 下列运算结果为x⁶的是（）

A、x³+x³ B、（x³）³ C、x·x⁵ D、x¹²÷x²

查看试题解析
2. 新冠病毒变异毒株奥密克戎直径约为0.00000011米，用科学记数法表示其直径约为（）

A、1.1×10^-6米 B、-1.1×10⁶米 C、1.1×10^-7米 D、-1.1×10⁷米

查看试题解析
3. 如图，能判定EB∥AC的条件是（）

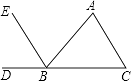A、∠C=∠ABE B、∠A=∠EBD C、∠C=∠ABC D、∠A=∠ABE

查看试题解析
4. 下列调查适合普查的是（）

A、了解中央电视台直播北京奥运会开幕式的全国收视率情况 B、了解一批袋装食品是否含有防腐剂 C、了解某县初中学生周末参加社区活动的时间 D、对新型冠状病毒肺炎患者的同一车厢的乘客进行医学检查

查看试题解析
5. 下列分式中，与 $\frac{y}{3 x}$ 相等的是（）

A、 $\frac{y^{2}}{3 x^{2}}$ B、 $\frac{2 x y}{6 x^{2}}$ C、 $- \frac{- y}{- 3 x}$ D、 $\frac{x y}{6 x^{2}}$

查看试题解析
6. 下列多项式因式分解正确的是（）

A、x²+y²=（x+y）² B、x²-6x+9=x（x-6）+9 C、-x²-2xy-y²=-（x-y）² D、2x²+xy-y²=（2x-y）（x+y）

查看试题解析
7. 已知长、宽分别为x，y的长方形周长为6，面积为1，则（x-y）²的值为（）

A、5 B、7 C、11 D、13

查看试题解析
8. 若x²-bx-10=（x+5）（x-a），则a^b的值是（）

A、-8 B、8 C、 $\frac{1}{8}$ D、 $- \frac{1}{8}$

查看试题解析
9. 一家工艺品厂按计件方式结算工资．暑假里，大学生小华去这家工艺品厂打工，第一天得到工资60元，第二天比第一天多做了10件，得到工资75元．如果设小华第二天做了x件，依题意列方程正确的是（）

A、 $\frac{60}{x} = \frac{75}{x - 10}$ B、 $\frac{60}{x - 10} = \frac{75}{x}$ C、 $\frac{60}{x} = \frac{75}{x + 10}$ D、 $\frac{60}{x + 10} = \frac{75}{x}$

查看试题解析
10. 如图a∥b，c与b相交，d与a相交，下列说法错误的是（）

A、∠4-∠2=∠3-∠1 B、若∠1+∠4=180，则∠2=∠3 C、∠1-∠2+∠3+∠4=180° D、若∠1=∠2，则∠3+∠4=180°

查看试题解析

二、填空题（本题有6小题，每小题3分，共18分）

11. 因式分解：a²-9=.

查看试题解析
12. 当x=时，分式 $\frac{x + 1}{x - 1}$ 的值为0．

查看试题解析
13. 如图是701班同学参加课外兴趣小组的扇形统计图，则表示参加“美术”课外兴趣小组的扇形的圆心角是度．

查看试题解析
14. 已知|x-3|+y²+4y+4=0，则x-y的值为．

查看试题解析
15. 如图，将△ABC沿着BC方向向右平移2个单位得到三角形△DEF，若△ABC的周长等于8，则四边形ABFD的周长是．

查看试题解析
16. 一组数据a₁ ， a₂ ， a₃ ， ……，满足以下规律：
a₁= $\frac{k + 1}{k}$ （k为正整数），a₂= $\frac{1}{1 - a_{1}}$ ，……，a_n= $\frac{1}{1 - a_{n - 1}}$ （n≥2）．则：

(1)、a₂=（用含k的代数式表示）；

(2)、当k=2时，a₂₀₂₂的值是．

查看试题解析

三、解答题（本题有8小题，第17~22题每题6分，第23~24题每题8分，共52分，各小题都必须写出解答过程）

17.

(1)、m⁸÷m⁵×（2m）³

(2)、化简：（2a-3）（2a+3）-2a（3a-1）

查看试题解析
18. 如图，点A，B在数轴上且点A在点B的左侧，它们所对应的数分别是 $\frac{4 - x}{x - 3}$ 和 $\frac{2}{3 - x}$

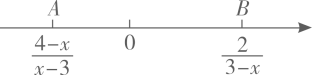(1)、当x=2.5时，求AB的长；

(2)、若点B到原点的距离比A到原点的距离多2，求x的值．

查看试题解析

19. 在一次社会调查活动中，小华收集到某“健步走运动”团队中20名成员一天行走的步数，记录如下：

5640 6430 6520 6798 7325 8430 8215 7453 7446 6754

7638 6834 7326 6830 8648 8753 9450 9865 7290 7850

对这20个数据按组距1000进行分组，并统计整理，绘制了如下尚不完整的统计图表：

步数分布统计表

组别	步数分组	频数
A	5500≤x<6500	2
B	6500≤x<7500	10
C	7500≤x<8500	m
D	8500≤x<9500	3
E	9500≤x<10500	n

根据以上信息解答下列问题

(1)、填空：m= ， n=；

(2)、补全频数分布直方图；

(3)、若该团队共有120人，请估计其中一天行走步数不少于7500步的人数．

查看试题解析

20. 在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的三个顶点A，B，C都在格点上．现将△ABC平移，使点A平移到点D，点E，F分别是B，C的对应点．

(1)、在图中画出平移后的△DEF：

(2)、△DFF的面积是；

(3)、在网格中找格点P，使S_△ABC=S_△BCP ，这样的格点P有个．

查看试题解析
21. 已知关于x，y的方程组 ${\begin{cases} x + 3 y = 7 \\ x - 3 y + m x + 3 = 0 \end{cases}$

(1)、写出方程x+3y=7的所有正整数解；

(2)、若方程组的解满足2x-3y=1，求m的值：

(3)、无论m取何值，方程x-3y+mx+3=0总有一个公共解，求出这个方程的公共解．

查看试题解析
22. 如图，已知∠1+∠2=180°，∠3=∠B，且∠AFE=50°．

(1)、求证：FD∥AB：

(2)、求∠ACB的度数．

查看试题解析
23. 一张如图1的长方形铁皮，四个角都剪去边长为30厘米的正方形，再四周折起，做成一个有底无盖的铁盒如图2，铁盒底面长方形的长是4a （cm），宽是3a （cm），这个无盖铁盒各个外表面的面积之和称为铁盒的全面积．

(1)、请用a的代数式表示图2中铁盒的全面积；

(2)、若铁盒的底面积是全面积的 $\frac{3}{4}$ ，求a的值；

(3)、若铁盒的全面积是底面积的正整数倍，求出这个正整数a的值．

查看试题解析
24. 如图①，已知AB∥CD，一条直线分别交AB，CD于点E，F，∠B=∠EFB=35°，FH⊥FB，点Q在BF上，连结QH．

(1)、求∠EFD的度数；

(2)、请说明FH平分∠GFD的理由．

(3)、若∠FQH=30°，将△FHQ绕着点F顺时针旋转，如图②，当边FH转至线段FE上时停止转动，记旋转角为α，请直接写出当α为多少度时，QH与△EBF的某一边平行?

查看试题解析