浙江省台州市温岭市等四市联考2020-2021学年八年级下学期期末数学试卷
试卷更新日期:2022-06-14 类型:期末考试
一、单选题
-
1. 下列电视台的台标,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 中的取值范围是( )A、 B、 C、 D、3. 直线与轴的交点坐标为( )A、 B、 C、 D、4. 如图所示, , 则数轴上点表示的数为( )
2. 中的取值范围是( )A、 B、 C、 D、3. 直线与轴的交点坐标为( )A、 B、 C、 D、4. 如图所示, , 则数轴上点表示的数为( ) A、3 B、5 C、 D、5. 正方形有而矩形不一定有的性质是( )A、四个角都是直角 B、对角线相等 C、对角线互相平分 D、对角线互相垂直6. 若可以合并为一项,则可以是( )A、6 B、12 C、15 D、187. 如图,在平行四边形中,对角线、相交于点 , 是边的中点, , 则( ).
A、3 B、5 C、 D、5. 正方形有而矩形不一定有的性质是( )A、四个角都是直角 B、对角线相等 C、对角线互相平分 D、对角线互相垂直6. 若可以合并为一项,则可以是( )A、6 B、12 C、15 D、187. 如图,在平行四边形中,对角线、相交于点 , 是边的中点, , 则( ). A、1 B、2 C、4 D、88. 某商场招聘员工一名,现有甲、乙、丙三人竞聘,通过计算机、语言和商品知识三项测试,他们各自成绩(百分制)如下表所示,若商场需要招聘负责将商品拆装上架的人员,对计算机、语言和商品知识分别赋权2,3,5,那么从成绩看,应该录取( )
A、1 B、2 C、4 D、88. 某商场招聘员工一名,现有甲、乙、丙三人竞聘,通过计算机、语言和商品知识三项测试,他们各自成绩(百分制)如下表所示,若商场需要招聘负责将商品拆装上架的人员,对计算机、语言和商品知识分别赋权2,3,5,那么从成绩看,应该录取( )应试者
计算机
语言
商品知识
甲
60
70
80
乙
80
70
60
丙
70
80
60
A、甲 B、乙 C、丙 D、任意一人都可9. 如图,阴影部分是一个菱形剪去一个平行四边形后所剩下的,要想知道阴影部分的周长,需要测量线段( ) 的长度. A、与 B、与 C、 D、10. 如图有两张等宽的矩形纸片,矩形不动,将矩形按如下方式缠绕:如图所示,先将点与点重合,再先后沿、对折,点、点所在的相邻两边不重叠、无空隙,最后点刚好与点重合,则图中两张纸片的长度之比( )
A、与 B、与 C、 D、10. 如图有两张等宽的矩形纸片,矩形不动,将矩形按如下方式缠绕:如图所示,先将点与点重合,再先后沿、对折,点、点所在的相邻两边不重叠、无空隙,最后点刚好与点重合,则图中两张纸片的长度之比( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算:= .
12. 将直线 向下平移2个单位长度,得到直线的解析式为 .13. 新冠疫情期间,小李同学连续两周居家健康检测,如下图是小李记录的体温情况折线统计图,记第一周体温的方差为 , 第二周体温的方差为 , 试判断两者之间的大小关系(用“>”、“=”、“<”填空).小李连续两周居家体温测量折线统计图
 14. 一次函数 , 当时,有最大值为5,则.15. 如图,是正方形内一点,四边形与也都是正方形,图中阴影部分的面积是10,则.
14. 一次函数 , 当时,有最大值为5,则.15. 如图,是正方形内一点,四边形与也都是正方形,图中阴影部分的面积是10,则. 16. 在数学综合实践课中,小明和同学对类似八下教科书25页例2的问题进行拓展探索:
16. 在数学综合实践课中,小明和同学对类似八下教科书25页例2的问题进行拓展探索:如图1,一根长为5米的木棍斜靠在一竖直的墙上,为4米,如果木棍的顶端沿墙下滑米,底端向外移动米,下滑后的木棍记为 , 则与满足的等式 , 即关于的函数解析式为 , 小明利用画图软件画出了该函数图象如图2,
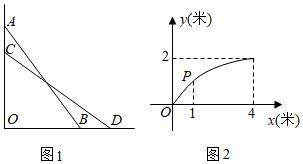 (1)、请写出图象上点的坐标(1,)(2)、根据图象,当的取值范围为时,的周长大于的周长.
(1)、请写出图象上点的坐标(1,)(2)、根据图象,当的取值范围为时,的周长大于的周长.三、解答题
-
17. 计算:(1)、;(2)、.18. 如图, , , ;
 (1)、求的长;(2)、求证:19. 滑车以1.5米/分钟的速度匀速地从轨道的一端滑向另一端,已知轨道的长为6米,滑车滑行分钟时离终点的路程为米.(1)、求关于的函数关系式,并写出自变量的取值范围;(2)、滑行多长时间时,滑车离终点1米?20. 如图,网格中每个小正方形的边长都是1,线段的两端点、都在格点上;
(1)、求的长;(2)、求证:19. 滑车以1.5米/分钟的速度匀速地从轨道的一端滑向另一端,已知轨道的长为6米,滑车滑行分钟时离终点的路程为米.(1)、求关于的函数关系式,并写出自变量的取值范围;(2)、滑行多长时间时,滑车离终点1米?20. 如图,网格中每个小正方形的边长都是1,线段的两端点、都在格点上; (1)、画出一个以为一边、面积为12的矩形;(要求:另外两个顶点也在格点上)(2)、画出一个以为一边、面积为9的三角形;(要求:另外一个顶点也要在格点上)21. 如图,在平行四边形中,是直线上的两点,;
(1)、画出一个以为一边、面积为12的矩形;(要求:另外两个顶点也在格点上)(2)、画出一个以为一边、面积为9的三角形;(要求:另外一个顶点也要在格点上)21. 如图,在平行四边形中,是直线上的两点,; (1)、求证:四边形是平行四边形;(2)、若四边形是矩形,且 , , , 求的长.22. 用水问题一直是台州人民关注的热点问题,为此,小明随机抽取自己家中一年5个月的月用水量(单位:吨),并对每个月的月平均气温(单位:进行了统计,得到下列统计图
(1)、求证:四边形是平行四边形;(2)、若四边形是矩形,且 , , , 求的长.22. 用水问题一直是台州人民关注的热点问题,为此,小明随机抽取自己家中一年5个月的月用水量(单位:吨),并对每个月的月平均气温(单位:进行了统计,得到下列统计图 (1)、小明家这5个月的月平均用水量为吨;(2)、下列推断:①当地当年月平均气温的众数是;
(1)、小明家这5个月的月平均用水量为吨;(2)、下列推断:①当地当年月平均气温的众数是;②当地当年月平均气温的中位数为;
③小明家这5个月的月用水量随着月平均气温的变化而变化,温度越高,月用水最越大.所有合理推断的序号是;
(3)、如果用小明家5月、7月、9月这三个月的月平均用水量估计当年的用水总量,你认为是否合理?并说明理由.23. 四边形中,对角线于点 , 且; (1)、如图1,若 , 求四边形的面积;(2)、如图2,若 , , 求;(3)、如图3,若 , , , 求四边形的面积.24. 公交公司员工小明住在站点的员工宿舍,每天早上去站点上班,站到站唯一一条公交线路示意图如图1,、、、是四个公交站点,其中、两站相距的路程是1200米,为了健身,小明往往沿公交线路步行到站或站后再乘公交车上班.
(1)、如图1,若 , 求四边形的面积;(2)、如图2,若 , , 求;(3)、如图3,若 , , , 求四边形的面积.24. 公交公司员工小明住在站点的员工宿舍,每天早上去站点上班,站到站唯一一条公交线路示意图如图1,、、、是四个公交站点,其中、两站相距的路程是1200米,为了健身,小明往往沿公交线路步行到站或站后再乘公交车上班. (1)、星期一,小明步行到站上车,记他距站的路程为米,离开站的时间为分,关于的函数图象如图2,求的解析式及公交车的速度;(2)、星期二,小明以与星期一相同出发时间和步行速度步行到站上车,已知公交车无论上行(→)还是下行(→)都每隔10分钟一班,每天始发时间和行车速度保持不变,乘客上下车时间忽略不计;
(1)、星期一,小明步行到站上车,记他距站的路程为米,离开站的时间为分,关于的函数图象如图2,求的解析式及公交车的速度;(2)、星期二,小明以与星期一相同出发时间和步行速度步行到站上车,已知公交车无论上行(→)还是下行(→)都每隔10分钟一班,每天始发时间和行车速度保持不变,乘客上下车时间忽略不计;①通过计算判断小明步行到达站时是否恰好有上行公交车到达站;
②小明到达站所用时间是星期一的1.5倍,求、两站相距的路程;
③若小明步行至站时刚好遇见一辆下行班车,这一趟上班途中,直接写出他遇到下行班车的最短间隔时间.