浙江省衢州市2020-2021学年八年级下学期期末数学试卷

试卷更新日期：2022-06-14 类型：期末考试

进入出卷网下载

一、单选题

1. 下面四个图标中，属于中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 二次根式 $\sqrt{x - 5}$ 中字母x的取值可以是（）

A、x＝0 B、x＝1 C、x＝2 D、x＝5

查看试题解析
3. 6位参加百米决赛的同学的成绩各不相同，按成绩取前3位设奖.如果小刘知道了自己的成绩后，要判断能否获奖，需知道其他5位同学成绩的（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
4. 若反比例函数 $y = \frac{k}{x}$ 的图象经过 $(2 ， - 1)$ ，则 $k$ 的值是（）

A、2 B、 $\frac{1}{2}$ C、-2 D、 $- \frac{1}{2}$

查看试题解析
5. 下列多边形中，内角和与外角和相等的是（）

A、三角形 B、四边形 C、五边形 D、六边形

查看试题解析
6. 某校为落实“光盘行动”，对每天的剩饭菜进行称重，第一周的剩余量为20kg，第三周为9.8kg，设每周剩余量的平均减少率为x，则可列方程（）

A、20（1﹣x）²＝9.8 B、20（1+x）²＝9.8 C、20（1﹣2x）＝9.8 D、20（1+2x）＝9.8

查看试题解析
7. 如图，在平行四边形ABCD中，∠ADC＝135°，∠CAD＝23°，则∠CAB等于（）

A、22° B、23° C、32° D、45°

查看试题解析
8. 如图，用尺规在矩形内作四边形ABCD，则下列结论不一定正确的是（）

A、AB＝AD B、AB＝BC C、AB＝AC D、AO＝CO

查看试题解析
9. 某杠杆装置如图，杆的一端吊起一桶水，阻力臂保持不变在使杠杆平衡的情况下，小康通过改变动力臂L，测量出相应的动力F数据如表.请根据表中数据规律探求，当动力臂L长度为2.0m时，所需动力最接近（）
动力臂L（m）
动力F（N）
0.5
600
1.0
302
1.5
200
2.0
a
2.5
120

A、120N B、151N C、300N D、302N

查看试题解析
10. 如图，四边形ABCD的对角线AC，BD相交于点O，AC⊥BD，E，F分别是AB，CD的中点，若AC＝BD＝2，则EF的长是（）

A、2 B、 $\sqrt{3}$ C、 $\frac{\sqrt{6}}{2}$ D、 $\sqrt{2}$

查看试题解析

二、填空题

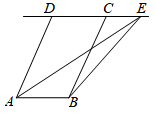
11. 计算 $\sqrt{(- 4)^{2}}$ 的结果是

查看试题解析
12. 用反证法证明“在三角形中至少有一个内角大于或等于60°”，应先假设命题不成立，即三角形的三个内角都60°（填“＞”“＜”或“＝”）.

查看试题解析
13. 一元二次方程x²+bx+2021＝0的一个根为x＝﹣1，则b的值为.

查看试题解析
14. 如图，AB∥CD，AB＝CD，若点E在直线CD上，△ABE的面积为30，则四边形ABCD的面积.

查看试题解析
15. 如图，在矩形ABCD中，E，F分别是边AB，BC上的点.将∠A，∠B，∠C按如图所示的方式向内翻折，EQ，EF，DF为折痕.若A，B，C恰好都落在同一点P上，AE＝1，则ED＝.

查看试题解析
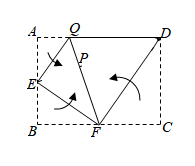16. 如图，点A，B在反比例函数y $= \frac{k}{x}$ 第一象限的图象上，点A坐标为（1，2），AB的延长线交x轴于点C.点D在x轴上，BD的延长线交双曲线的另一支于点E，AB＝BC＝BD.则点C的坐标为， △CDE的面积等于.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{12} + \sqrt{5} \times \sqrt{15}$ ；

(2)、 $\frac{2}{\sqrt{3} - 1}$ ．

查看试题解析
18. 解方程：

(1)、（x﹣2）²＝9．

(2)、x（x﹣3）+x＝3．

查看试题解析
19. 如图，在▱ABCD中，E，F分别是BC，AD的中点，连结AE，CF.求证：AE＝CF.

查看试题解析
20. 某校举行“衢州有礼八个一”知识问答竞赛.每班选20名同学参加比赛，根据答对的题目数量，得分等级分为5分，4分，3分，2分，学校将八年级甲班和乙班的成绩整理并绘制成如下的统计图.

(1)、请把甲班知识问答成绩统计图补充完整；

(2)、通过统计得到如表，请求出表中数据a，b的值.
班级
平均数（分）
中位数（分）
众数（分）
甲班
a
4
4
乙班
3.6
3.5
b

(3)、根据（2）的结果，你认为甲，乙两班哪个班级成绩更好？写出你的理由.

查看试题解析
21. 如图，平行四边形ABCD放置在平面直角坐标系中，已知点A（﹣2，0），B（﹣6，0），D（0，3），点C在反比例函数y $= \frac{k}{x}$ 的图象上.

(1)、直接写出点C坐标，并求反比例函数的表达式；

(2)、将平行四边形ABCD向上平移得到平行四边形EFGH，使点F在反比例函数y $= \frac{k}{x}$ 的图象上，GH与反比例函数图象交于点M.连结AE，求AE的长及点M的坐标.

查看试题解析
22. △ABC是一块腰长为20cm的等腰直角三角形白铁皮零料.请你利用三角形零料裁出一块矩形白铁皮，并使矩形的四个顶点都在三角形的边上.
活动一：若裁出的矩形白铁皮的面积为零料面积的 $\frac{3}{8}$ ，请画出符合题意的裁剪示意图（一种即可），并求出此时矩形铁皮的边长.
活动二：根据“活动一”中你选择的裁剪方法，思考并解答：

(1)、是否能够使得裁出的矩形白铁皮的面积是零料面积的 $\frac{3}{4}$ ？请判断并说明理由；

(2)、猜想裁剪出的矩形白铁皮的面积最大值.直接写出结论，不必说理.

查看试题解析
23. 在正方形ABCD中，连结BD，O为BD中点，点E在线段OD上（不与点O，D重合）.

(1)、如图1，过点E作EF⊥AB于点F，EG⊥BC于点G.分别判断EF与EG的数量与位置关系，并说明理由.

(2)、如图2，连结EC，过点E作EH⊥EC，交AB于点H.
①求证：EH＝EC.
②猜想OE与BH的数量关系，并证明.

查看试题解析

班级	平均数（分）	中位数（分）	众数（分）
甲班	a	4	4
乙班	3.6	3.5	b

动力臂L（m）	动力F（N）
0.5	600
1.0	302
1.5	200
2.0	a
2.5	120