浙江省宁波市南三县2020-2021学年八年级下学期期末数学试卷

试卷更新日期：2022-06-14 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式中，为最简二次根式的是（）

A、 $\sqrt{5}$ B、 $\sqrt{8}$ C、 $\sqrt{12}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
2. 下列方程中，属于一元二次方程的是（）

A、x+1＝0 B、x²＝2x﹣1 C、2y﹣x＝1 D、x²+3＝ $\frac{2}{x}$

查看试题解析
3. 下面四个图标中，中心对称图形个数是（）

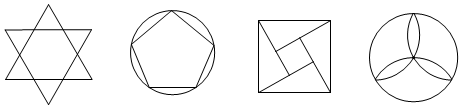A、0 B、1个 C、2个 D、3个

查看试题解析
4. 数据21、12、18、16、20、21的众数和中位数分别是( )

A、21和19 B、21和17 C、20和19 D、20和18

查看试题解析
5. 利用反证法证明命题“四边形中至少有一个角是钝角或直角”时，应假设（）

A、四边形中至多有一个内角是钝角或直角 B、四边形中所有内角都是锐角 C、四边形的每一个内角都是钝角或直角 D、四边形中所有内角都是直角

查看试题解析
6. 正方形具有而菱形不一定具有的性质是（）.

A、四条边都相等 B、对角线互相垂直且平分 C、对角线相等 D、对角线平分一组对角

查看试题解析
7. 已知函数y＝﹣ $\frac{3}{x}$ ，又x₁ ， x₂对应的函数值分别是y₁ ， y₂ ，若0＜x₁＜x₂ ，则有（）

A、0＜y₂＜y₁ B、0＜y₁＜y₂ C、y₁＜y₂＜0 D、y₂＜y₁＜0

查看试题解析
8. 如图，在 $△ A B C$ 中，D，E，F分别为BC，AC，AB边的中点， $A H ⊥ B C$ 于H， $H E = 8$ ，则DF等于（）

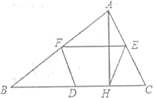A、4 B、8 C、12 D、16

查看试题解析
9. 欧几里得的《原本》记载，形如 $x^{2} + a x = b^{2}$ 的方程的图解法是：画 $R t Δ A B C$ ，使 $∠ A C B = 90^{\circ}$ ， $B C = \frac{a}{2}$ ， $A C = b$ ，再在斜边 $A B$ 上截取 $B D = \frac{a}{2}$ .则该方程的一个正根是（）

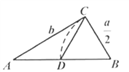A、 $A C$ 的长 B、 $A D$ 的长 C、 $B C$ 的长 D、 $C D$ 的长

查看试题解析
10. 如图，在一个大长方形中放入三个边长不等的小正方形①、②、③，若要求出两个阴影部分周长的差，只要知道下列哪个图形的面积（）

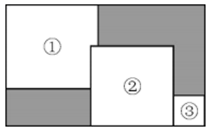A、正方形① B、正方形② C、正方形③ D、大长方形

查看试题解析

二、填空题

11. 若二次根式 $\sqrt{a + 1}$ 有意义，则 $a$ 的取值范围是.

查看试题解析
12. 五边形的外角和是度.

查看试题解析
13. 某招聘考试分笔试和面试两种，小明笔试成绩90分，面试成绩85分，如果笔试成绩、面试成绩按3：2计算，那么小明的平均成绩是分

查看试题解析
14. 若 $m$ 是方程 $x^{2} + x - 1 = 0$ 一个根，则代数式 $2 m^{2} + 2 m + 2021$ 的值为.

查看试题解析
15. 如图，点E为正方形ABCD外一点，且ED＝CD，连结AE，交BD于点F.若∠CDE＝30°，则∠DFC的度数为 .

查看试题解析
16. 如图，过原点的直线交反比例函数 $y = \frac{a}{x}$ 图象于 $P$ ， $Q$ 两点，过点 $P$ 分别作 $x$ 轴， $y$ 轴的垂线，交反比例函数 $y = \frac{b}{x}$ （ $x > 0$ ）的图象于 $A$ ， $B$ 两点.若 $b - a = 7$ ，则图中阴影部分的面积为.

查看试题解析

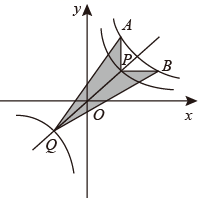
三、解答题

17.

(1)、计算： $\sqrt{45} - \sqrt{20} + \sqrt{\frac{1}{5}}$

(2)、 ${(\sqrt{2} - 1)}^{2} + (\sqrt{2} - 1) (1 + \sqrt{2})$

查看试题解析
18. 解方程：

(1)、 $2 x^{2} + 3 x = 0$ ；

(2)、 $x^{2} - 8 x - 9 = 0$

查看试题解析

19. 博才中学要从甲、乙两名同学中选拔一名同学代表学校参加“华罗庚金杯”数学竞赛活动.这两位活动同学最近四次的数学测验成绩如下表：（单位：分）

	第一次	第二次	第三次	第四次
甲	75	70	85	90
乙	85	82	75	78

(1)、根据表中数据，分别求出甲、乙两名同学这四次数学测验成绩的平均分.

(2)、经计算，甲、乙两位同学这四次数学测验成绩的方差分别为

S_{甲}^{2} = 62.5

，

S_{乙}^{2} = 14.5

，你认为哪位同学的成绩较稳定?请说明理由.

查看试题解析

20. 矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F，H在菱形ABCD的对角线BD上.

(1)、求证：BG＝DE；

(2)、若E为AD中点，FH＝4，求菱形ABCD的周长.

查看试题解析
21. 如图，已知在平面直角坐标系中， $O$ 是坐标原点，点 $A (2 ， 5)$ 在反比例函数 $y_{1} = \frac{k}{x}$ 的图象上.一次函数 $y_{2} = x + b$ 的图象经过点 $A$ ，且与反比例函数图象的另一交点为 $B$ .

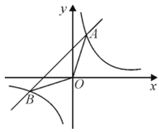(1)、求反比例函数和一次函数的解析式；

(2)、根据图象直接写出 $y_{1} > y_{2}$ 时， $x$ 的取值范围.

查看试题解析
22. 某超市销售一种饮料，平均每天可售出100箱，每箱利润120元．天气渐热，为了扩大销售，增加利润，超市准备适当降价．据测算，若每箱饮料每降价1元，每天可多售出2箱．针对这种饮料的销售情况，请解答以下问题：

(1)、当每箱饮料降价20元时，这种饮料每天销售获利多少元？

(2)、在要求每箱饮料获利大于80元的情况下，要使每天销售饮料获利14400元，问每箱应降价多少元？

查看试题解析
23. 在正方形ABCD中，AB＝4，点E是边AD上一动点，以CE为边，在CE的右侧作正方形CEFG，连结BF.

(1)、如图1，当点E与点A重合时，则BF的长为.

(2)、如图2，当AE＝1时，求点F到AD的距离和BF的长.

(3)、当BF最短时，请直接写出此时AE的长.

查看试题解析
24. 我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”.

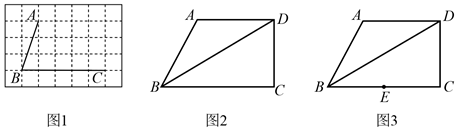(1)、如图1，四边形 $A B C D$ 的顶点 $A$ ， $B$ ， $C$ 在网格格点上，请你在 $5 \times 7$ 的网格中分别画出3个不同形状的等邻边四边形 $A B C D$ ，要求顶点 $D$ 在网格格点上.

(2)、如图2， $A D ⊥ D C$ ， $∠ C = 90 °$ ， $B D$ 平分 $∠ A B C$ ，求证：四边形 $A B C D$ 为“等邻边四边形”.

(3)、如图3，在（2）的条件下， $∠ A B C = 60 °$ ， $C D = 2$ ， $E$ 是 $B C$ 的中点，点 $M$ 是 $B D$ 边上一点，当四边形 $C E M D$ 是“等邻边四边形”时，求 $B M$ 的长.

查看试题解析