浙江省金华市东阳市2020-2021学年八年级下学期期末数学试卷
试卷更新日期:2022-06-14 类型:期末考试
一、单选题
-
1. 化简的结果为( )A、3 B、-3 C、81 D、-812. 下列四个图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 用配方法解一元二次方程x2-4x-7=0,可变形为( )A、(x-2)2=7 B、(x-2)2=11 C、(x+2)2=7 D、(x+2)2=114. 一个多边形的内角和是外角和的 倍,则这个多边形是( )A、六边形 B、五边形 C、四边形 D、七边形5. 某校进行广播操比赛,如图是20位评委给某班的评分情况统计图,则该班平均得分( )
3. 用配方法解一元二次方程x2-4x-7=0,可变形为( )A、(x-2)2=7 B、(x-2)2=11 C、(x+2)2=7 D、(x+2)2=114. 一个多边形的内角和是外角和的 倍,则这个多边形是( )A、六边形 B、五边形 C、四边形 D、七边形5. 某校进行广播操比赛,如图是20位评委给某班的评分情况统计图,则该班平均得分( )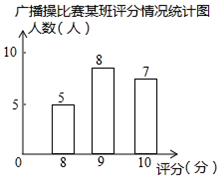 A、9 B、6.67 C、9.1 D、6.746. 如图,点B在反比例函数 ( )的图象上,点C在反比例函数 ( )的图象上,且 轴, ,垂足为点C , 交y轴于点A , 则 的面积为 ( )
A、9 B、6.67 C、9.1 D、6.746. 如图,点B在反比例函数 ( )的图象上,点C在反比例函数 ( )的图象上,且 轴, ,垂足为点C , 交y轴于点A , 则 的面积为 ( )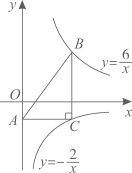 A、3 B、4 C、5 D、67. 用反证法证明命题“在三角形中,至少有一个内角大于或等于60°”时,先假设( )A、每个内角都小于60° B、每个内角都大于60° C、没有一个内角小于等于60° D、每个内角都等于60°8. 如图,函数 与函数 的图象相交于点 .若 ,则x的取值范围是( )
A、3 B、4 C、5 D、67. 用反证法证明命题“在三角形中,至少有一个内角大于或等于60°”时,先假设( )A、每个内角都小于60° B、每个内角都大于60° C、没有一个内角小于等于60° D、每个内角都等于60°8. 如图,函数 与函数 的图象相交于点 .若 ,则x的取值范围是( )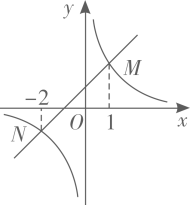 A、 或 B、 或 C、 或 D、 或9. 某厂家2020年1~5月份的口罩产量统计如图所示.设2月份到4月份,该厂家口罩产量的平均月增长率为x,根据题意可得方程( )
A、 或 B、 或 C、 或 D、 或9. 某厂家2020年1~5月份的口罩产量统计如图所示.设2月份到4月份,该厂家口罩产量的平均月增长率为x,根据题意可得方程( )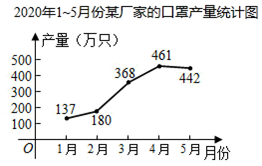 A、368(1﹣x)2=180 B、180(1+x)2=461 C、461(1﹣x)2=180 D、368(1+x)2=44210. 将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=6 , E,F分别是边AC,BC上的动点,当四边形DEBF为平行四边形时,该四边形的面积是( )
A、368(1﹣x)2=180 B、180(1+x)2=461 C、461(1﹣x)2=180 D、368(1+x)2=44210. 将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=6 , E,F分别是边AC,BC上的动点,当四边形DEBF为平行四边形时,该四边形的面积是( )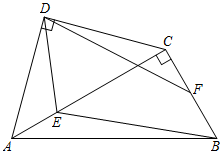 A、3 B、6 C、 D、81
A、3 B、6 C、 D、81二、填空题
-
11. 二次根式中字母的取值范围是 .12. 某果农随机从甲、乙、丙三个品种的批把树中各选5棵,每棵产量的平均数(单位:千克)及方差(单位:千克2)如表所示,他准备从这三个品种中选出一种产量既高又稳定的批把树进行种植,则应选的品种是 .
甲
乙
丙
45
45
42
S2
1.8
2.3
1.8
13. 若y= , 则x+y的值为 .14. 已知x为实数,且满足 ,那么x2+3x=.
15. 如图,平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为6,4,反比例函数y= (x>0)的图象经过A,B两点,若菱形ABCD的面积为2 ,则k的值为 .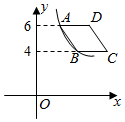 16. 在综合实践课上,小明把边长为2cm的正方形纸片沿着对角线AC剪开,如图l所示.然后固定纸片△ABC,把纸片△ADC沿AC的方向平移得到△A′D′C′,连A′B,D′B,D′C,在平移过程中:
16. 在综合实践课上,小明把边长为2cm的正方形纸片沿着对角线AC剪开,如图l所示.然后固定纸片△ABC,把纸片△ADC沿AC的方向平移得到△A′D′C′,连A′B,D′B,D′C,在平移过程中: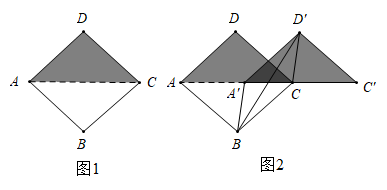 (1)、四边形A′BCD′的形状始终是;(2)、A′B+D′B的最小值为.
(1)、四边形A′BCD′的形状始终是;(2)、A′B+D′B的最小值为.三、解答题
-
17. 计算:(1)、;(2)、.18. 解方程:(1)、3x2-4x+1=0.(2)、(y-3)2=(2y-1)(y-3).19. 已知关于x的方程:x2﹣(6+m)x+9+3m=0.(1)、求证:无论m为何值,方程都有实数根.(2)、若该方程的两个实数根恰为斜边为5的直角三角形的两直角边长,求m的值.20. 6月4日,我市教育局发布了“珍爱生命,预防溺水”-致全市市民的倡议书.某校为了解全校学生对防溺水措施的熟悉情况,随机抽查了部分学生进行了《防溺水学习手册》10题问答测试,并把答对题数制成统计表和扇形统计图(如图所示).
答对题数
6
7
8
9
10
人数(人)
20
28
m
16
12

请根据统计图表中的信息,解答下列问题:
(1)、求被抽查的学生人数和m的值.(2)、求本次抽查的学生答对题数的中位数和众数.(3)、若该校共有800名学生,根据抽查结果,估计该校学生答对10题的人数.(4)、根据该校学生《防溺水学习手册》测试数据分析,请你对该校提出一条建议.21. 如图,平行四边形ABCD的对角线交于点O,以OD,CD为邻边作平行四边形DOEC,OE交BC于点F,连结BE.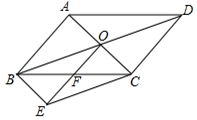 (1)、求证:四边形BECO是平行四边形.(2)、若OB⊥AC,OF=4,求平行四边形ABCD的周长.22. 有两张长12cm,宽10cm的矩形纸板,分别按照图1与图2两种方式裁去若干小正方形和小矩形,剩余部分(阴影部分)恰好做成无盖和有盖的长方体纸盒各一个.
(1)、求证:四边形BECO是平行四边形.(2)、若OB⊥AC,OF=4,求平行四边形ABCD的周长.22. 有两张长12cm,宽10cm的矩形纸板,分别按照图1与图2两种方式裁去若干小正方形和小矩形,剩余部分(阴影部分)恰好做成无盖和有盖的长方体纸盒各一个.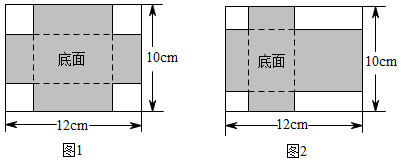 (1)、做成有盖长方体纸盒的裁剪方式是(填“图1”或“图2”).(2)、已知图1中裁去的小正方形边长为1.5cm,求做成的纸盒的底面积.(3)、已知按图2裁剪方式做成纸盒的底面积为24cm2 , 则剪去的小正方形的边长为多少cm?23. 如图,在矩形ABCD中,已知点A(2,1),且AB=4,AD=3,把矩形ABCD的内部及边上,横、纵坐标均为整数的点称为靓点,反比例函数y=(x>0)的图象为曲线L.
(1)、做成有盖长方体纸盒的裁剪方式是(填“图1”或“图2”).(2)、已知图1中裁去的小正方形边长为1.5cm,求做成的纸盒的底面积.(3)、已知按图2裁剪方式做成纸盒的底面积为24cm2 , 则剪去的小正方形的边长为多少cm?23. 如图,在矩形ABCD中,已知点A(2,1),且AB=4,AD=3,把矩形ABCD的内部及边上,横、纵坐标均为整数的点称为靓点,反比例函数y=(x>0)的图象为曲线L.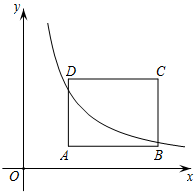 (1)、若曲线L过AB的中点.
(1)、若曲线L过AB的中点.①求k的值.
②求该曲线L下方(包括边界)的靓点坐标.
(2)、若分布在曲线L上方与下方的靓点个数相同,求k的取值范围.24. 如图,直线y=﹣x+11分别交x轴y轴于A,B两点,点D以每秒2个单位的速度从点A出发沿射线AD方向运动,同时点E以每秒1个单位的速度从点B出发沿边BA方向运动,当E到达点A时,点D,E同时停止运动,设运动时间为t秒.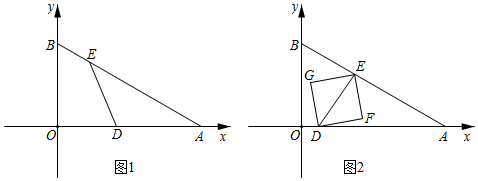 (1)、求点A的坐标及线段AB的长.(2)、如图1,当t=4﹣2时,求∠AED的度数.(3)、如图2,以DE为对角线作正方形DFEG,在运动过程中,是否存在正方形DFEG的一边恰好落在△ADB的一边上?若存在,请求出所有符合条件的t值;若不存在,请说明理由.
(1)、求点A的坐标及线段AB的长.(2)、如图1,当t=4﹣2时,求∠AED的度数.(3)、如图2,以DE为对角线作正方形DFEG,在运动过程中,是否存在正方形DFEG的一边恰好落在△ADB的一边上?若存在,请求出所有符合条件的t值;若不存在,请说明理由.