浙江省杭州市拱墅区锦绣育才教育集团2020-2021学年八年级下学期期末数学试卷

试卷更新日期：2022-06-14 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个图形是国际通用的交通标志，其中既是中心对称图形，又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列方程属于一元二次方程的是（）

A、 $x y + x^{2} = 9$ B、 $a x^{2} + b x + c = 0$ C、 $\frac{1}{x} - \frac{1}{x^{2}} = 5$ D、 $7 x + 6 = x^{2}$

查看试题解析
3. 下列命题中，真命题是（）

A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、顺次连接四边形的各边中点所得的四边形是平行四边形 D、两条对角线互相平分且相等的四边形是正方形

查看试题解析
4. 某班3位同学进行投篮比赛，每人投10次，平均每人投中8次，已知第一、三位同学分别投中8次，10次，那么第二位同学投中（）

A、6次 B、7次 C、8次 D、9次

查看试题解析
5. 用反证法证明“三角形中必有一个内角不小于60°”时，应当假设这个三角形中（）

A、有一个内角小于60° B、每一个内角都小于60° C、有一个内角大于60° D、每一个内角都大于60°

查看试题解析
6. 若关于x的一元二次方程（k﹣1）x²﹣2kx+k﹣3＝0有实数根，则k的取值范围为（）

A、k≥0 B、k≥0且k≠1 C、k≥ $\frac{3}{4}$ D、k≥ $\frac{3}{4}$ 且k≠1

查看试题解析
7. 如图，在矩形ABCD中，对角线AC，BD相交于点O，DE⊥AC于点E，∠EDC：∠EDA＝1：2，且AC＝8，则EC的长度为（）

A、2 $\sqrt{3}$ B、2 C、4 D、 $\sqrt{3}$

查看试题解析
8. 若反比例函数y＝ $\frac{a - 1}{x}$ （a＞1，x＜0）图象上有两个点（x₁ ， y₁），（x₂ ， y₂），设m＝（x₁﹣x₂）（y₁﹣y₂），则y＝mx﹣m不经过第（）象限.

A、一 B、二 C、三 D、四

查看试题解析
9. 已知函数y=ax²-2ax-1（a是常数且a≠0），下列结论正确的是（）

A、当a=1时，函数图象过点(-1，1) B、当a= -2时，函数图象与x轴没有交点 C、当a $> 0$ ，则当x $\geq$ 1时，y随x的增大而减小 D、当a $< 0$ ，则当x $\leq$ 1时，y随x的增大而增大

查看试题解析
10. 已知边长为2cm的菱形AFEO，∠AFE＝120°，过点O作两条夹角为60°的射线，分别交边AF，边FE于点M，N，连接MN，则下列命题正确的是（）
①S_四_边_形OMFN＝ $\sqrt{3}$ cm²；②MN的长度为定值；③△OMN的形状为等边三角形；④ $\frac{S_{Δ O M N}}{S_{Δ F M N}}$ 的最小值为3.

A、①③ B、①②③④ C、③④ D、①③④

查看试题解析

二、填空题

11. 若式子 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 在解一元二次方程x²+bx+c＝0时，小明看错了一次项系数b，得到的解为x₁＝1，x₂＝2；小刚看错了常数项c，得到的解为x₁＝3，x₂＝4.请你写出正确的一元二次方程 .

查看试题解析
13. 据统计，某车间10名员工每人日平均生产零件个数为6，方差为2.5，引入新技术后，每名员工每日都比原先多生产1个零件，则现在日平均生产零件个数为，方差为 .

查看试题解析
14. 如图，在平行四边形ABCD中，E为边CD上的一个点，将△ADE沿AE折叠至△AD′E处，AD′与CE交于点F，若∠B＝50°，∠DAE＝20°，则∠FED′的大小为 .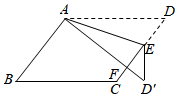

查看试题解析
15. 如果抛物线y＝x²﹣6x+c﹣1的顶点到x轴的距离是4，则c的值等于 .

查看试题解析
16. 在平面直角坐标系xOy中，对于不在坐标轴上的任意一点P(x，y)，我们把点P′ $(\frac{1}{x} ， \frac{1}{y})$ 称为点P的“倒影点”．直线y＝－x＋1上有两点A，B，它们的“倒影点”A′，B′均在反比例函数y＝ $\frac{k}{x}$ 的图象上．若AB＝2 $\sqrt{2}$ ，则k＝．

查看试题解析

三、解答题

17.

(1)、计算：﹣ $\sqrt{2}$ + $\sqrt{24}$ × $\frac{1}{\sqrt{3}}$

(2)、解方程：3x(x+4)＝2(x+4)

查看试题解析
18. 学校抽查了某班级某月份其中5天的用电量，数据如下表（单位：度）：
度数
9
10
11
天数
3
1
1

(1)、求这5天用电量的平均数，众数，中位数.

(2)、学校共有30个班级，若根据学生在校时间该月按22天计，试估计该校该月的总用电量.

查看试题解析
19. 已知：线段a，b.

(1)、尺规作图：作出一个菱形，使它的边长为a，另一条对角线为b（要求：保留作图痕迹，不写作法）；

(2)、若a＝5，b＝8，求该菱形的高线长.

查看试题解析
20. 一商店销售某种商品，平均每天可售出20件，每件盈利40元.为了扩大销售、增加盈利，该店采取了降价措施，在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件.

(1)、若销售单价降低5元，那么平均每天销售数量为多少件？

(2)、若该商店每天销售利润为1200元，问每件商品可降价多少元？

查看试题解析
21. 如图，在平行四边形ABCD中，∠ABC，∠BCD的平分线分别交AD于点E，F，线段BE，CF相交于点G.

(1)、问：线段BE与CF的位置关系，并说明理由；

(2)、若AB＝3，CF＝4，求BE的长.

查看试题解析
22. 已知反比例函数 $y_{1} = \frac{k}{x}$ 的图象经过 $(3 ， 2)$ ， $(m ， n)$ 两点.

(1)、求 $y_{1}$ 的函数表达式；

(2)、当 $m < 1$ 时，求 $n$ 的取值范围；

(3)、设一次函数 $y_{2} = a x - 3 a + 2 (a > 0)$ ，当 $x > 0$ 时，比较 $y_{1}$ 与 $y_{2}$ 的大小.

查看试题解析
23. 已知正方形ABCD，点F是射线DC上一动点（不与C、D重合），连接AF并延长交直线BC于点E，交BD于H，连接CH，过点C作CG⊥HC交AE于点G.

(1)、若点F在边CD上，如图1.
①证明：∠DAH＝∠DCH；
②猜想 $△$ GFC的形状并说明理由.

(2)、取DF中点M，连结MG.若MG＝5，正方形边长为8，求BE的长.

查看试题解析

度数	9	10	11
天数	3	1	1