四川省眉山市2020-2021学年八年级下学期期末数学试卷
试卷更新日期:2022-06-14 类型:期末考试
一、单选题
-
1. 若分式有意义,则的取值范围是( )A、 B、 C、 D、2. 下列各式计算正确的是( )A、 B、 C、 D、3. 甲,乙,丙,丁四人进行射击测试,射击成绩的平均数都约为8.8环,方差分别为 , , , , 则四人中成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁4. 下列说法正确的是( )A、对角线互相垂直平分的四边形是菱形 B、对角线相等的四边形是矩形 C、对角线相等且互相垂直的四边形是正方形 D、一组对边相等且一组对角相等的四边形是平行四边形5. 点在直线上,则点关于轴对称的点的坐标为( )A、 B、 C、 D、6. 某鞋店试销一种新款男鞋,试销期间销售情况如下表:
鞋的尺码()
24
24.5
25
.5.5
26
26.5
销售数量(双)
2
7
18
10
8
3
则该组数据的下列统计量中,对鞋店下次进货最具有参考意义的是( )
A、中位数 B、平均数 C、众数 D、方差7. 如图,在中, , , 垂足为 , 若 , 则的度数为( ) A、 B、 C、 D、8. 如图,在菱形ABCD中,点E,F分别在AB,CD上,且 ,连接EF交BD于点O连接AO.若 ,则 的度数为( )
A、 B、 C、 D、8. 如图,在菱形ABCD中,点E,F分别在AB,CD上,且 ,连接EF交BD于点O连接AO.若 ,则 的度数为( )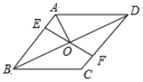 A、50° B、55° C、65° D、75°9. 一次函数 与反比例函数 在同一坐标系中的图象可能是( )A、
A、50° B、55° C、65° D、75°9. 一次函数 与反比例函数 在同一坐标系中的图象可能是( )A、 B、
B、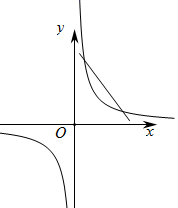 C、
C、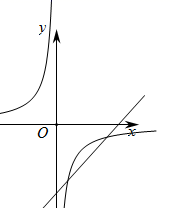 D、
D、 10. 如图,在矩形中,的平分线交的延长线于点 , 若 , , 则的长为( )
10. 如图,在矩形中,的平分线交的延长线于点 , 若 , , 则的长为( ) A、3.5 B、4 C、4.5 D、511. 若关于x的方程 1的解为正数,则所有符合条件的正整数a的个数为( )A、1个 B、2个 C、3个 D、4个12. 如图,正方形的对角线 , 交于点 , 是上的一点,连接 , 过点作于点 , 交于点 , 交于点.下列结论:①;②;③;④当为中点时, , 其中正确的是( )
A、3.5 B、4 C、4.5 D、511. 若关于x的方程 1的解为正数,则所有符合条件的正整数a的个数为( )A、1个 B、2个 C、3个 D、4个12. 如图,正方形的对角线 , 交于点 , 是上的一点,连接 , 过点作于点 , 交于点 , 交于点.下列结论:①;②;③;④当为中点时, , 其中正确的是( ) A、①②③ B、①②④ C、①③④ D、①②③④
A、①②③ B、①②④ C、①③④ D、①②③④二、填空题
-
13. 从2019年底,新型冠状病毒肺炎在全球迅猛传播,被世界卫生组织定为“国际关注的突发公共卫生事件”.据研究,这次疫情的冠状病毒微粒直径大约在0.12微米左右,0.12微米等于0.00000012米,数字0.00000012用科学记数法表示为.14. 小宁的数学期末总评成绩由平时、期中、期末考试成绩按权重比组成.如果小宁本学期三项成绩依次为90分、85分、95分,则小宁本学期的数学期末总评成绩是分.15. 如图,在矩形中,点在上,将矩形沿折叠,使点落在边上的点处.若 , , 则的长为.
 16. 如图,直线经过点 , 当时,的取值范围是.
16. 如图,直线经过点 , 当时,的取值范围是. 17. 如图,菱形的周长为40,对角线.过的中点作交于点 , 交的延长线于点 , 则的长为.
17. 如图,菱形的周长为40,对角线.过的中点作交于点 , 交的延长线于点 , 则的长为. 18. 两个反比例函数y= 和y= 在第一象限内的图象如图所示,点P1 , P2 , P3 , ……P2021在反比例函数y= 的图象上,它们的纵坐标分别为y1 , y2 , y3 , ……,y2021 , 横坐标分别为2,4,6,……共2021个偶数,过点P1 , P2 , P3 , ……P2021分别作y轴的垂线,与y= 的图象交点依次为Q1(x1 , y1),Q2(x2 , y2),Q3(x3 , y3),……,Q2021(x2021 , y2021), 则x2021=
18. 两个反比例函数y= 和y= 在第一象限内的图象如图所示,点P1 , P2 , P3 , ……P2021在反比例函数y= 的图象上,它们的纵坐标分别为y1 , y2 , y3 , ……,y2021 , 横坐标分别为2,4,6,……共2021个偶数,过点P1 , P2 , P3 , ……P2021分别作y轴的垂线,与y= 的图象交点依次为Q1(x1 , y1),Q2(x2 , y2),Q3(x3 , y3),……,Q2021(x2021 , y2021), 则x2021=
三、解答题
-
19. 解方程:20. 先化简,再求值: , 其中.21. 如图,在中, , , , 是的中点,是的中点,过点作交的延长线于点.
 (1)、求证:四边形是平行四边形;(2)、求四边形的面积.22. 如图,直线与轴交于点 , 与轴交于点 , 将直线向下平移后经过点.
(1)、求证:四边形是平行四边形;(2)、求四边形的面积.22. 如图,直线与轴交于点 , 与轴交于点 , 将直线向下平移后经过点. (1)、求平移后的直线所对应的函数表达式;(2)、求的面积.23. 某中学举办“信息技术知识竞赛”,甲队、乙队根据初赛成绩各选出5名选手参加学校决赛,两支队伍选出的5名选手的决赛成绩如下:
(1)、求平移后的直线所对应的函数表达式;(2)、求的面积.23. 某中学举办“信息技术知识竞赛”,甲队、乙队根据初赛成绩各选出5名选手参加学校决赛,两支队伍选出的5名选手的决赛成绩如下:甲队:75,80,85,85,100;
乙队:70,100,100,75,80
(1)、根据数据填写下表:平均分(分)
中位数(分)
众数(分)
方差
甲队
85
85
70
乙队
80
根据表格信息填空: , , ;
(2)、计算乙队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.24. 为了做好学校疫情防控工作,某校从药店购进一批甲、乙两种型号的口罩,已知乙种型号的口罩每袋单价比甲种型号的口罩每袋单价少5元,购买2500元的甲种口罩的数量和购买2000元的乙种口罩的数量相同.(1)、求甲、乙两种口罩每袋的售价;(2)、根据学校防疫需要,学校拟从该药店购进甲、乙两种型号口罩共800袋,其中乙种型号的数量不超过甲种型号的3倍.问学校应如何购买,才能使得购买口罩所需费用最少?并求出所需的最少费用.25. 如图,反比例函数的图象与经过原点的直线AB的一个交点为A( , n).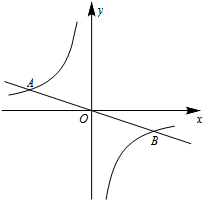 (1)、求直线AB对应的函数表达式;(2)、点C在y轴上,当△ABC的面积为6时,求点C的坐标;(3)、在直线AB上方的平面内是否存在点D,使△ABD为等腰直角三角形?若存在,请直接写出点D的坐标;若不存在,请说明理由.26. 如图,在菱形ABCD中,∠A=60°,AD=2,点E是AD边上一点(点E不与点A、D重合),点F在AB的延长线上,且BF=DE,连结EF交BD于点G.
(1)、求直线AB对应的函数表达式;(2)、点C在y轴上,当△ABC的面积为6时,求点C的坐标;(3)、在直线AB上方的平面内是否存在点D,使△ABD为等腰直角三角形?若存在,请直接写出点D的坐标;若不存在,请说明理由.26. 如图,在菱形ABCD中,∠A=60°,AD=2,点E是AD边上一点(点E不与点A、D重合),点F在AB的延长线上,且BF=DE,连结EF交BD于点G. (1)、求证:△BDE≌△CBF;(2)、求证:EG=GF;(3)、设DE=x,DG=y,求y关于x的函数表达式,并直接写出x的取值范围.
(1)、求证:△BDE≌△CBF;(2)、求证:EG=GF;(3)、设DE=x,DG=y,求y关于x的函数表达式,并直接写出x的取值范围.