四川省广元市苍溪县2020-2021学年八年级下学期期末数学试卷

试卷更新日期：2022-06-14 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式中，运算正确的是（）

A、 $\sqrt{(- 2)^{2}}$ ＝﹣2 B、 $\sqrt{2}$ + $\sqrt{8}$ ＝ $\sqrt{10}$ C、 $\sqrt{2}$ × $\sqrt{8}$ ＝4 D、2﹣ $\sqrt{2} = \sqrt{2}$

查看试题解析
2. 下列四组线段中，能组成直角三角形的是（　　）.

A、a=1，b=2，c=3 B、a=2，b=3，c=4 C、a=2，b=4，c=5 D、a=3，b=4，c=5

查看试题解析
3. 函数y=2x﹣5的图象经过（）

A、第一、三、四象限 B、第一、二、四象限 C、第二、三、四象限 D、第一、二、三象限

查看试题解析
4. 某市一周日最高气温如图所示，则该市这周的日最高气温的众数是（）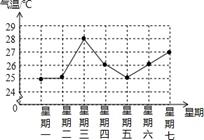

A、25 B、26 C、27 D、28

查看试题解析
5. 要得到函数y=2x+3的图象，只需将函数y=2x的图象（）

A、向左平移3个单位 B、向右平移3个单位 C、向下平移3个单位 D、向上平移3个单位

查看试题解析
6. 如图，在矩形ABCD中，对角线AC，BD交于点O，已知∠AOD=120°，AB=2，则AC的长为（）

A、2 B、4 C、6 D、8

查看试题解析
7. 已知P₁（﹣3，y₁），P₂（2，y₂）是一次函数y=﹣x﹣1的图象上的两个点，则y₁ ， y₂的大小关系是（）

A、y₁=y₂ B、y₁＜y₂ C、y₁_＞y₂ D、不能确定

查看试题解析
8. 一家公司打算招聘一名翻译对甲、乙、丙三名应试者进行了听、说、读、写的英语水平测试，他们各项成绩（百分制）如下表所示：
应试者
听
说
读
写
甲
73
80
82
83
乙
85
78
85
73
丙
80
82
80
80
如果这家公司想招一名笔译能力较强的翻译，听、说、读、写成绩按照2：1：3：4的比确定，从他们的平均成绩（百分制）看，应该录取（）

A、甲 B、乙 C、丙 D、不确定

查看试题解析
9. 如图，已知：函数y＝3x+b和y＝ax﹣3的图象交于点P（﹣2，﹣5），则根据图象可得不等式3x+b＞ax﹣3的解集是（）

A、x＞﹣5 B、x＞﹣2 C、x＞﹣3 D、x＜﹣2

查看试题解析
10. 设max表示两个数中的最大值，例如： $\max {0 ， 2} = 2$ ， $\max {12 ， 8} = 12$ ，则关于 $x$ 的函数 $y = \max {3 x ， 2 x + 1}$ 可表示为（）

A、 $y = 3 x$ B、 $y = 2 x + 1$ C、 $y = {\begin{array}{l} 3 x (x < 1) \\ 2 x + 1 (x \geq 1) \end{array}$ D、 $y = {\begin{array}{l} 2 x + 1 (x < 1) \\ 3 x (x \geq 1) \end{array}$

查看试题解析

二、填空题

11. 若 $\sqrt{x + 2}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 已知一组数据x₁ ， x₂ ， x₃ ， x₄ ， x₅的平均数是2，那么另一组数据3x₁﹣2，3x₂﹣2，3x₃﹣2，3x₄﹣2，3x₅﹣2的平均数是．

查看试题解析
13. 计算 $a \sqrt{\frac{3}{a}} + \sqrt{9 a} - \frac{3 \sqrt{a}}{\sqrt{3}}$ = ．

查看试题解析
14.
如图，两张等宽的纸条交叉叠放在一起，若重合部分构成的四边形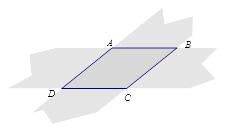 $A B C D$ 中， $A B = 3$ ， $A C = 2$ ，则 $B D$ 的长为

查看试题解析
15. 如图，点A在线段BG上，四边形ABCD和四边形DEFG都是正方形，面积分别是10和19，则△CDE的面积为.

查看试题解析
16. 一次函数y₁＝kx+b与y₂＝x+a的图象如图，则下列结论：①k $<$ 0；②a $>$ 0；③关于x的方程kx﹣x＝a﹣b的解是x＝3；④当x $>$ 3时，y₁ $<$ y₂中．则正确的序号有．

查看试题解析

三、解答题

17. 计算： $\sqrt{27} - | - 2 \sqrt{3} | - \sqrt{3} {(2 - π)}^{0} + {(- 1)}^{2018}$

查看试题解析
18. 小明根据学习函数的经验，对函数y＝﹣|x|+3的图象与性质进行了探究.下面是小明的探究过程，请你解决相关问题.

(1)、如表y与x的几组对应值：
x
…
﹣4
﹣3
﹣2
﹣1
0
1
2
3
4
…
y
…
﹣1
0
1
2
3
2
1
a
﹣1
…
①a＝；
②若A（b，﹣7），B（10，﹣7）为该函数图象上不同的两点，则b＝；

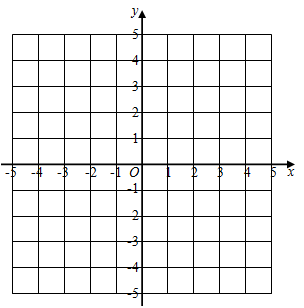
(2)、如图，在平面直角坐标系中，描出以上表中各对对应值为坐标的点，并根据描出的点，画出该函数的图象：
①该函数有 ▲ （填“最大值”或“最小值”）；并写出这个值为 ▲ ；
②求出函数图象与坐标轴在第二象限内所围成的图形的面积；
③观察函数y＝﹣|x|+3的图象，写出该图象的两条性质.

查看试题解析
19. 如图所示的一块地，已知 $A D = 4 m$ ， $C D = 3 m$ ， $A D ⊥ D C$ ， $A B = 13 m$ ， $B C = 12 m$ ，求这块地的面积.

查看试题解析
20. 如图，在▱ABCD中，E是AD的中点，延长CB到点F，使 $B F = \frac{1}{2} B C$ ，连接BE、AF.

(1)、完成画图并证明四边形AFBE是平行四边形；

(2)、若AB=6，AD=8，∠C=60°，求BE的长.

查看试题解析

21. 我市某中学举行“中国梦•校园好声音”歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.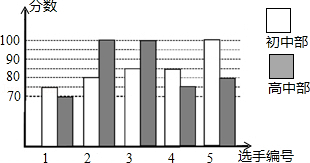

(1)、根据图示填写下表；

	平均数（分）	中位数（分）	众数（分）
初中部		85
高中部	85		100

(2)、结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；

(3)、计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.

查看试题解析

22. 如图，在平行四边形ABCD中，点E是边BC的中点，连接AE并延长，交DC的延长线于点F，连接AC，BF.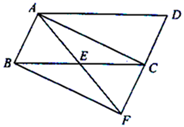

(1)、求证：△ABE≌△FCE；

(2)、当四边形ABFC是矩形时，若∠AEC＝120°，求∠D的度数.

查看试题解析
23. 如图，一次函数y＝ax+b的图象与正比例函数y＝kx的图象交于点M ，

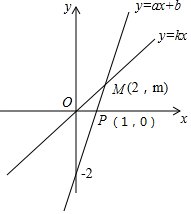(1)、求正比例函数和一次函数的解析式；

(2)、根据图象写出使正比例函数的值大于一次函数的值的x的取值范围；

(3)、求△MOP的面积．

查看试题解析
24. 如图，矩形ABCD的对角线AC、BD交于点O，且DE∥AC，CE∥BD．

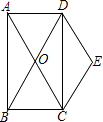(1)、求证：四边形OCED是菱形；

(2)、若∠BAC=30°，AC=4，求菱形OCED的面积．

查看试题解析
25. 学校计划从某苗木基地购进A、B两咱树苗共200棵绿化校园.已知购买了3棵A种树苗和5棵B种树苗共需700元；购买2棵A种树苗和1棵B种树苗共需280元.

(1)、每棵A种树苗、B种树苗各需多少元？

(2)、学校除支付购买树苗的费用外，平均每棵树苗还需支付运输及种植费用20元.设学校购买B种树苗x棵，购买两种树苗及运输、种植所需的总费用为y元，求y与x的函数关系；

(3)、在（2）的条件下，若学校用于绿化的总费用在22400元限额内，且购买A种树苗的数量不少于B种树苗的数量，请给出一种费用最省的方案，并求出该方案所需的费用.

查看试题解析
26. 已知：甲乙两车分别从相距300千米的A、B两地同时出发相向而行，其中甲到达B地后立即返回，如图是它们离各自出发地的距离y（千米）与行驶时间x（小时）之间的函数图象．

(1)、求甲车离出发地的距离y_甲（千米）与行驶时间x（小时）之间的函数关系式，并写出自变量的取值范围；

(2)、它们出发 $\frac{9}{2}$ 小时时，离各自出发地的距离相等，求乙车离出发地的距离y_乙（千米）与行驶时间x（小时）之间的函数关系式，并写出自变量的取值范围；

(3)、在（2）的条件下，求它们在行驶的过程中相遇的时间．

查看试题解析

应试者	听	说	读	写
甲	73	80	82	83
乙	85	78	85	73
丙	80	82	80	80

x	…	﹣4	﹣3	﹣2	﹣1	0	1	2	3	4	…
y	…	﹣1	0	1	2	3	2	1	a	﹣1	…