四川省广安市五县（市）2020-2021学年八年级下学期期末质量监测数学试卷

试卷更新日期：2022-06-14 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各组数中，是勾股数的是（）

A、6，8，10 B、4，6，8 C、0.3 ，0.4，0.5 D、3 ，6 ，9

查看试题解析
2. 学校舞蹈队有12名队员，他们的年龄情况如表：
年龄/岁
12
13
14
15
人数/人
2
4
3
3
则这个舞蹈队中队员年龄的众数和中位数分别是（）

A、13，13.5 B、13，13 C、13，14 D、14，13

查看试题解析
3. 下列运算正确的是（）

A、 $\sqrt{12} \div \sqrt{6} = 2$ B、 $\sqrt{8} + \sqrt{2} = 2 \sqrt{2}$ C、 $\sqrt{12} \times \sqrt{3} = 6$ D、 $\sqrt{5} - \sqrt{3} = \sqrt{2}$

查看试题解析
4. 如图，在▱ABCD中，若EF $/ /$ AD，OH $/ /$ CD，EF与GH相交于点O，则图中的平行四边形一共有（）

A、4个 B、5个 C、8个 D、9个

查看试题解析
5. 对于一次函数y＝﹣3x+2，下列说法中正确的是（）

A、y随着x的增大而增大 B、该函数图象与y轴的交点坐标为(0，2) C、点(1，1)在该函数的图象上 D、该函数图象经过第二、三、四象限

查看试题解析
6. 如图，在 $△$ ABC中，∠ACB＝90°，D是AB边的中点，CE⊥AB于点E.若CE＝5，CD＝6，则 $△$ ABC的面积是（）

A、60 B、50 C、40 D、30

查看试题解析
7. 周末，小依骑自行车从家去北辰湖公园游玩，中途自行车出现了故障，恰好路边有便民服务点可以修车，车修好后，她继续骑车前往目的地.设她从家出发后所用时间为t（min），所骑行的路程为s（m），s与t之间的函数关系如图所示.对于下列说法：
①小依中途休息了2min；②小依修车前骑车的平均速度为400m/min；③小依在上述过程中骑行的路程为4000m；④小依修车前骑车的平均速度小于修车后骑车的平均速度.其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC，PF⊥CD，垂足分别为点E，F，连接AP，EF，给出下列四个结论：①AP＝EF；②∠PFE＝∠BAP；③PD＝ $\sqrt{2}$ EC；④ $△$ APD一定是等腰三角形.其中正确的结论有（）

A、①②④ B、①②③ C、②③④ D、①②③④

查看试题解析

二、填空题

9. 若 $b = \sqrt{2 - a} + \sqrt{a - 2} - 5$ ，则 $a - b =$ ．

查看试题解析
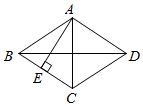
10. 将一次函数y＝﹣2x+4的图象向下平移5个单位长度后，所得图象对应的函数表达式为.

查看试题解析
11. 已知在 $△$ ABC中，D，E，F分别是AB，AC，BC边的中点，连接DE，DF，EF.若DE＝3cm，DF＝4cm，EF＝5cm，则 $△$ ABC的面积为cm².

查看试题解析
12. 如图，已知菱形ABCD的对角线AC，BD的长分别是4cm，6cm，AE⊥BC，垂足为E，则AE的长是cm.

查看试题解析
13. 如图，已知四边形A，B，C，D，E都是正方形，图中所有的三角形都是直角三角形.若正方形A，B，D的面积依次为4，6，15，则正方形C的面积为.

查看试题解析

三、解答题

14. 计算： $(5 + 2 \sqrt{6}) (5 - 2 \sqrt{6}) + 4 \times \sqrt{\frac{1}{2}} - \sqrt{32}$ .

查看试题解析
15. 如图，在四边形 $A B C D$ 中， $A D / / B C$ ，点E为 $C D$ 边上的中点连接 $A E$ 并延长，与 $B C$ 的延长线交于点F，连接 $A C$ 、 $D F$ ，求证：四边形 $A C F D$ 是平行四边形.

查看试题解析
16. 如图，在平面直角坐标系中，直线l₁：y＝3x与直线l₂：y＝kx+b交于点A(a，3)，点B(2，4)在直线l₂上.

(1)、求a的值及直线l₂的函数解析式；

(2)、直接写出关于x的不等式kx+b＜3x的解集.

查看试题解析

四、八年级抽取的学生每日英语阅读时间的统计量

五、

17. 学校为了了解本校七、八年级学生每日英语阅读的时间情况，从七、八年级中各随机抽查了20名学生进行问卷调查，将调查结果进行整理、描述和分析，并将其分为五组（单位：min）：A（0≤t＜20），B（20≤t＜40），C（40≤t＜60），D（60≤t＜80），E（80≤t＜100）.
下面给出了部分信息：
七年级抽取的在C组学生每日英语阅读时间（单位：min）分别为40，40，50，55.
八年级抽取的20名学生的每日英语阅读时间（单位：min）分别为10，15，20，25，30，35，40，40，45，50，50，50，55，60，60，75，75，80，90，95.
七、八年级抽取的学生每日英语阅读时间的统计量

平均数众数中位数方差

七年级 50 35 a 580

八年级 50 b 50 560

根据以上信息，解答下列问题：

(1)、a＝， b＝， m＝；

(2)、根据方差数据，你认为哪个年级的学生每日英语阅读的情况较好？请说明理由.

查看试题解析
18. 为积极响应垃圾分类的号召，某街道决定在街道内的所有小区安装垃圾分类的温馨提示牌和垃圾箱.已知购买3个垃圾箱和2个温馨提示牌需要280元，购买2个垃圾箱和3个温馨提示牌需要270元.

(1)、每个垃圾箱和每个温馨提示牌各多少元？

(2)、若购买垃圾箱和温馨提示牌共100个（两种都买），且垃圾箱的个数不少于温馨提示牌个数的3倍，请写出总费用w（元）与垃圾箱个数m（个）之间的函数关系式，并说明当购买垃圾箱和温馨提示牌各多少个时，总费用最低，最低费用为多少元？

查看试题解析
19. 观察下列各式及其变形过程： $a_{1} = \frac{1}{\sqrt{2} + 2 \sqrt{1}} = 1 - \frac{1}{\sqrt{2}}$ ， $a_{2} = \frac{1}{2 \sqrt{3} + 3 \sqrt{2}} = \frac{1}{\sqrt{2}} - \frac{1}{\sqrt{3}}$ ， $a_{3} = \frac{1}{3 \sqrt{4} + 4 \sqrt{3}} = \frac{1}{\sqrt{3}} - \frac{1}{\sqrt{4}}$ .

(1)、按照此规律和格式，请你写出第五个等式的变形过程： $a_{5} =$ ；

(2)、请通过计算验证（1）中 $a_{5}$ 变形过程的正确性；

(3)、按照此规律，计算 $(a_{1} + a_{2} + a_{3} + \cdot \cdot \cdot + a_{n}) (a_{1} - a_{2} - a_{3} - \cdot \cdot \cdot - a_{n} + \sqrt{2})$ 的值.

查看试题解析
20. 如图，在Rt $△$ ABC中，∠B＝90°，AC＝40cm，∠A＝60°，点D从点C出发沿CA方向以4cm/s的速度匀速运动，点A为终点；点E从点A出发沿AB方向以2cm/s的速度匀速运动，点B为终点.两点同时出发，当其中一点到达终点时，另一点也随之停止运动.设点D，E的运动时间是t（s）（0＜t≤10）.过点D作DF⊥BC于点F，连接DE，EF.

(1)、在运动过程中，四边形AEFD能否成为菱形？如果能，求出相应的t值；如果不能，请说明理由.

(2)、当t为何值时， $△$ DEF为直角三角形？请说明理由.

(3)、当四边形DEBF是矩形时，直接写出四边形DEBF的面积.

查看试题解析

	平均数	众数	中位数	方差
七年级	50	35	a	580
八年级	50	b	50	560

年龄/岁	12	13	14	15
人数/人	2	4	3	3