四川省成都市高新区2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-06-14 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，属于中心对称图形的是（）

A、角 B、等边三角形 C、平行四边形 D、正五边形

查看试题解析
2. 分式 $\frac{x + 5}{x - 2}$ 的值是零，则 $x$ 的值为（）

A、5 B、-5 C、-2 D、2

查看试题解析
3. 若 $x > y$ ，则下列不等式一定成立的是（）.

A、 $x - 6 < y - 6$ B、 $3 x < 3 y$ C、 $- 2 x < - 2 y$ D、 $2 x + 1 < 2 y + 1$

查看试题解析
4. 如图，在 $▱ A B C D$ 中， $∠ A B C = 125 °$ ， $∠ C A D = 21 °$ .则 $∠ C A B$ 的度数是（）

A、21° B、34° C、35° D、55°

查看试题解析
5. 下列由左边到右边的变形，属于因式分解的是（）

A、 $(a + 1) (a - 1) = a^{2} - 1$ B、 $a^{2} + a + 1 = a (a + 1) + 1$ C、 $a m + b m = m (a + b)$ D、 $a^{2} + 2 a + 4 = {(a + 2)}^{2}$

查看试题解析
6. 如图，在 $△ A B C$ 中， $∠ B A C > 90 °$ . $A B$ 的垂直平分线交 $B C$ 于点 $E$ ， $A C$ 的垂直平分线交 $B C$ 于点 $F$ ，连接 $A E$ 、 $A F$ ，若 $△ A E F$ 的周长为2.则 $B C$ 的长是（）

A、2 B、3 C、4 D、无法确定

查看试题解析
7. 如图，已知在 $△ A B C$ 中， $D$ ， $E$ ， $F$ 分别是边 $B C$ ， $C A$ ， $A B$ 的中点， $A B = 10$ ， $A C = 8$ ，则四边形AFDE的周长等于（）

A、18 B、16 C、14 D、12

查看试题解析
8. 下列命题是假命题的是（）

A、到线段两端点距离相等的点在该线段的垂直平分线上 B、一个锐角和一条边分别相等的两个直角三角形全等 C、有一个角等于60°的等腰三角形是等边三角形 D、三角形三条角平分线交于一点，并且这一点到三条边的距离相等

查看试题解析
9. 一次环保知识竞赛共有20道选择题，答对一题得5分；答错或不答，每题扣1分.要使总得分不少于88分，则至少要答对几道题？若设答对 $x$ 道题，可列出的不等式为（）

A、 $5 x - (20 - x) > 88$ B、 $5 x - (20 - x) < 88$ C、 $5 x - x \geq 88$ D、 $5 x - (20 - x) \geq 88$

查看试题解析
10. 如图，在Rt $△ A B C$ 中， $∠ C A B = 50 °$ ，点 $D$ 在斜边 $A B$ 上，如果 $△ A B C$ 绕点 $B$ 旋转后与 $△ E B D$ 重合，连接 $A E$ ，那么 $∠ E A B$ 的度数是（）

A、80° B、70° C、60° D、50°

查看试题解析

二、填空题

11. 若 $\frac{m}{n} = \frac{1}{2}$ ，则 $\frac{2 m}{m + n}$ 的值是.

查看试题解析
12. 如图，直线 $y = a x$ 与直线 $y = k x + 3$ 交于点 $P (1 ， 2)$ ，则关于 $x$ 的不等式 $a x > k x + 3$ 的解集为.

查看试题解析
13. 如图所示是个三个相同的正 $n$ 边形拼成的无缝隙、不重叠的图形的一部分，则 $n$ 的值为.

查看试题解析
14. 如图，在 $△ A B C$ 中， $A C = B C$ ， $∠ C = 90 °$ ， $A D$ 是 $△ A B C$ 的角平分线，已知 $C D = 4$ .则 $A C$ 的长为.

查看试题解析
15. 若 $a = b + 1$ ，则代数式 $a^{2} - 2 a b + b^{2} + 2$ 的值为.

查看试题解析
16. 已知关于 $x$ 的方程 $3 x + a = x - 5$ 的解是正数，则实数 $a$ 的取值范围是.

查看试题解析
17. 甲、乙两位采购员同去一家面粉公司购买两次面粉，两次面粉的价格有变化，两位采购员的购货方式也不同，其中，甲每次购买800kg，乙每次用去600元，而不管购买多少面粉.设两次购买的面粉单价分别为 $a$ 元/kg和 $b$ 元/kg（ $a$ ， $b$ 是正数，且 $a \neq b$ ），那么甲所购面粉的平均单价是元，在甲、乙所购买面粉的平均单价中，高的平均单价与低的平均单价的差值为.（结果用含 $a$ ， $b$ 的代数式表示，需化为最简形式）

查看试题解析
18. 如图 $△ A B C$ 为等边三角形，点 $D$ 是 $△ A B C$ 边 $A B$ 上一点，且 $B D = \sqrt{3} A D$ .将 $△ A B C$ 绕点 $D$ 按逆时针方向旋转 $β ° (0 < β < 180)$ 后，若点 $B$ 恰好落在初始等边 $△ A B C$ 的边上，则 $β$ 的值为.

查看试题解析
19. 如图，四边形 $A B C D$ 是平行四边形， $∠ C = 60 °$ ， $\frac{A B}{B C} = \frac{\sqrt{13}}{6}$ ，点 $F$ 在 $B C$ 上，且 $C F = \frac{1}{3} B C$ ，点 $E$ 为边 $C D$ 上的一动点，连接 $E F$ ， $A E$ ，将 $△ C E F$ 沿直线 $E F$ 翻折，点 $C$ 的对应点为点 $G$ ，连接 $B G$ ，若点 $B$ ，点 $G$ ，点 $E$ 在同条直线上，则 $\frac{A E}{D E}$ 的值为.

查看试题解析

三、解答题

20.

(1)、因式分解： $a x^{2} - 4 a y^{2}$ .

(2)、解不等式组： ${\begin{array}{l} 2 x + 5 \leq 3 (x + 2) \\ \frac{x - 1}{2} < \frac{x}{3} \end{array}$ .

查看试题解析
21. 解方程： $\frac{y - 2}{y - 3} = 2 - \frac{1}{3 - y}$ .

查看试题解析
22. 先化简，再求值： $(1 - \frac{n + 1}{m + 1}) \div \frac{m^{2} - 2 m n + n^{2}}{2 m - 2 n}$ ，其中 $m = \sqrt{2} - 1$ .

查看试题解析
23. 如图，四边形 $A B C D$ 各顶点的坐标分别为 $A (- 3 ， 5)$ ， $B (- 4 ， 3)$ ， $C (- 1 ， 1)$ ， $D (- 1 ， 4)$ .

⑴以原点 $O$ 为对称中心，画出与四边形 $A B C D$ 成中心对称的四边形；

⑵将四边形 $A B C D$ 先向上平移3个单位长度，再向右平移4个单位长度，得到四边形 $A_{2} B_{2} C_{2} D_{2}$ .

①画出四边形 $A_{2} B_{2} C_{2} D_{2}$ ；

②如果将四边形 $A_{2} B_{2} C_{2} D_{2}$ 看成是由四边形 $A B C D$ 经过斜向上方向一次平移得到的，请直接写出这一平移的平移距离.

查看试题解析
24. 如图， $▱ A B C D$ 的对角线 $A C$ 与 $B D$ 相交于点 $O$ ，点 $E$ ， $F$ 分别在 $O B$ 和 $O D$ 上，且 $∠ A E B = ∠ C F D$ ．

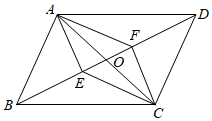(1)、求证：四边形 $A E C F$ 是平行四边形；

(2)、若 $∠ A E B = 90 °$ ， $A E = 4$ ．且 $∠ E A F = 45 °$ ，求线段 $A C$ 的长．

查看试题解析
25. 在学习了图形的旋转知识后，某数学兴趣小组对教材中有关图形旋转的问题进行了进一步探究.

(1)、问题梳理，问题呈现：如图1，点 $D$ 在等边 $△ A B C$ 的边 $B C$ 上，过点 $C$ 画 $A B$ 的平行线 $l$ ，在 $l$ 上取 $C E = B D$ ，连接 $A E$ ，则在图1中会产生一对旋转图形.请结合问题中的条件，证明： $△ A B D ≌ △ A C E$ ；

(2)、初步尝试：如图2，在 $△ A B C$ 中， $A B = A C$ ，点 $D$ 在 $B C$ 边上，且 $B D < D C$ ，将 $△ A B D$ 沿某条直线翻折，使得 $A B$ 与 $A C$ 重合，点 $D$ 与 $B C$ 边上点 $F$ 重合，再将 $△ A C F$ 沿 $A C$ 所在直线翻折，得到 $△ A C E$ ，则在图2中会产生一对旋转图形.若 $∠ B A C = 30 °$ ， $A D = 6$ ，连接 $D E$ ，求 $△ A D E$ 的面积；

(3)、深入探究：如图3，在 $△ A B C$ 中， $∠ A C B = 60 °$ ， $∠ B A C = 75 °$ ， $A C = 6$ ，点 $D$ 是边 $B C$ 上的任意一点，连接 $A D$ ，将线段 $A D$ 绕点 $A$ 按逆时针方向旋转75°，得到线段 $A E$ ，连接 $C E$ ，求线段 $C E$ 长度的最小值.

查看试题解析
26. 某商家预测一种应季衬衫能畅销市场，就4000元购进一批这种衬衫，这种衬衫面市后果然供不应求，商家又8800元购进了第二批这种衬衫，所购数量是第一批购进数量的2倍，但单价贵了4元.

(1)、该商家购进的两批衬衫数量分别是多少件？

(2)、商家销售这种衬衫时每件定价都是60元，经过一段时间后，根据市场销售情况，商家决定对最后剩余的20件衬衫进行打折出售，要使这两批衬衫全部售出后的总利润不少于4960元，则最后剩余的20件衬衫出售至多可打几折？

查看试题解析
27. 如图1，四边形 $A B C D$ 是正方形，点 $E$ 在边 $A B$ 上任意一点（点 $E$ 不与点 $A$ ，点 $B$ 重合），点 $F$ 在 $A D$ 的延长线上， $B E = D F$ .

(1)、求证： $C E = C F$ ；

(2)、如图2，作点 $D$ 关于 $C F$ 的对称点 $G$ ，连接 $B G$ 、 $C G$ 、 $D G$ ， $D G$ 与 $C F$ 交于点 $P$ ， $B G$ 与 $C F$ 交于点 $H$ .与 $C E$ 交于点 $Q$ .
①若 $∠ B C E = 20 °$ ，求 $∠ C H B$ 的度数；
②用等式表示线段 $C D$ ， $G H$ ， $B H$ 之间的数量关系，并说明理由.

查看试题解析
28. 如图1，在平面直角坐标系 $x O y$ 中，直线 $l_{1}$ 与 $x$ 轴交于点 $A (m ， 0)$ ，与 $y$ 轴交于点 $B (0 ， m n)$ （ $m < 0$ ， $n > 0$ ）.

(1)、若 $m = - 4$ ， $n = \frac{1}{2}$ ，求直线 $l_{1}$ 的表达式；

(2)、如图2，在（1）的条件下，直线 $l_{2}$ ： $y = \frac{1}{2} x$ 与直线 $l_{1}$ 交于点 $C$ ，点 $D (0 ， 2)$ .直线 $l_{2}$ 上是否存在一点 $G$ ，使得 $\frac{S_{△ A C D}}{S_{△ C D G}} = \frac{4}{3}$ ？若存在，请求出点 $G$ 的坐标；若不存在，请说明理由；

(3)、在直线 $l_{1}$ 下方有一点 $P$ ，其横坐标为 $m + n$ ，连接 $P B$ ，若 $∠ P B A = 2 ∠ B A O$ ，求 $\frac{n}{O A}$ 的取值范围.

查看试题解析