浙江省台州市温岭、天台、临海、玉环2020-2021学年七年级下学期期末数学试卷

试卷更新日期：2022-06-14 类型：期末考试

进入出卷网下载

一、单选题

1. 在下列实数中，属于无理数的是（）

A、 $3$ B、 $\sqrt{2}$ C、 $0$ D、 $\frac{2}{3}$

查看试题解析
2. 下列各点中，在第三象限的点是（）

A、 $(1 ， 2)$ B、 $(1 ， - 2)$ C、 $(- 1 ， 2)$ D、 $(- 1 ， - 2)$

查看试题解析
3. 下列各组 $x$ ， $y$ 的值，（）是二元一次方程 $x + 2 y = 3$ 的解.

A、 ${\begin{array}{l} x = 1 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = - 1 \end{array}$ C、 ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ D、 ${\begin{array}{l} x = - 2 \\ y = \frac{1}{2} \end{array}$

查看试题解析
4. 把不等式 $2 - x \geq 0$ 的解集表示在数轴上，正确的是（）

A、 B、 C、 D、

查看试题解析
5. 某学校计划筹备美食节，为了解学生最喜欢吃的水果，调查组设计了调查问卷（不完整）：准备在“①热带水果；②草莓；③火龙果；④西瓜；⑤无核水果”中选取 $3$ 种作为该调查问卷的备选项目，你认为合理的是（）

A、①②③ B、①③⑤ C、②③④ D、②④⑤

查看试题解析
6. 在同一平面内，将两个完全相同的等腰直角三角板如图所示摆放（一条直角边部分重合），可以画出两条互相平行的直线a，b，这样操作的依据是（）

A、同位角相等，两直线平行 B、内错角相等，两直线平行 C、两直线平行，同位角相等 D、两直线平行，内错角相等

查看试题解析
7. 若 $x - y > 0$ ，则下列不等式一定成立的是（）

A、 $x + 3 < y + 3$ B、 $3 - x < 3 - y$ C、 $\frac{y}{x} < 1$ D、 $\frac{x}{y} < 1$

查看试题解析
8. 如图，三角形 $A B C$ 中， $∠ B A C = 90 °$ ， $A D ⊥ B C$ ，垂足为 $D$ ，则下列结论正确的是（）

A、点 $C$ 到 $A B$ 的垂线段是线段 $A B$ B、 $A D > A C$ C、点 $A$ 到 $B C$ 的距离是线段 $A D$ 的长度 D、 $A D < B D$

查看试题解析
9. 《孙子算经》中有一道题：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺.木长几何？”意思是：用一根绳子去量一根长木，绳子还剩 $4.5$ 尺；将绳子对折后再去量长木，长木还剩余 $1$ 尺.设木长 $x$ 尺，绳子长 $y$ 尺，则可得方程组（）

A、 ${\begin{array}{l} x = y + 4.5 \\ \frac{1}{2} x = y - 1 \end{array}$ B、 ${\begin{array}{l} y = x + 4.5 \\ \frac{1}{2} y = x - 1 \end{array}$ C、 ${\begin{array}{l} x = y + 4.5 \\ \frac{1}{2} y = x - 1 \end{array}$ D、 ${\begin{array}{l} y = x + 4.5 \\ \frac{1}{2} x = y - 1 \end{array}$

查看试题解析
10. 已知点 $A (- 3129 ， - 5079)$ ，将点 $A$ 作如下平移：第 $1$ 次将 $A$ 向右平移 $1$ 个单位，向上平移 $2$ 个单位得到 $A_{1}$ ；第 $2$ 次将 $A_{1}$ 向右平移 $2$ 个单位，向上平移 $3$ 个单位得到 $A_{2}$ ， $⋯$ ，第 $n$ 次将点 $A_{n - 1}$ 向右平移 $n$ 个单位，向上平移 $n + 1$ 个单位得到 $A_{n}$ ，则 $A_{100}$ 的坐标为（）

A、 $(2021 ， 71)$ B、 $(2021 ， 723)$ C、 $(1921 ， 71)$ D、 $(1921 ， 723)$

查看试题解析

二、填空题

11. 2020年末，我国完成了第7次人口普查，国家统计局采取的调查方式是.（填“全面调查”“抽样调查”）

查看试题解析
12. 点 $A (m + 1 ， 3 m - 7)$ 在第一、三象限的角平分线上，则 $m =$ .

查看试题解析
13. 一幅三角板如图摆放，点 $F$ 在 $B C$ 上， $B C / / D E$ ， $D E$ 交 $A B$ 于点 $M$ ，则 $∠ A M E =$ $°$ .

查看试题解析
14. 已知 $3.31 5^{2} = 10.989225$ ， $3.3 2^{2} = 11.0224$ ，则 $\sqrt{11} \approx$ .（精确到 $0.01$ ）

查看试题解析
15. 一个水池有 $A$ ， $B$ 两个水口，其中 $A$ 为进水口， $B$ 水口可进水也可出水（ $B$ 水口进出水速度相同）.已知单独打开 $A$ 进水口，需要 $t$ 小时将水池由空池注满.若将 $A$ ， $B$ 两个水口同时打开进水， $5$ 小时将水池由空池注满；若将 $A$ 水口打开进水，同时 $B$ 水口打开出水， $10$ 小时将水池由空池注满，则 $t =$ .

查看试题解析
16. 某校七年级有 $4$ 个班，共 $180$ 人，（1）班至（4）班的人数分别 $a$ ， $b$ ， $c$ ， $d$ $(a < b < c < d)$ .已知（1）班的人数不少于 $41$ 人，且 $b + c > a + d$ ，则（4）班人数为.

查看试题解析

三、解答题

17. 计算： $\sqrt{3} + | \sqrt{3} - 2 | - \sqrt{4}$ .

查看试题解析
18. 解下列方程组：

(1)、 ${\begin{array}{l} x + y = 3 \\ x - y = 1 \end{array}$

(2)、 ${\begin{array}{l} 2 (x + 1) + 3 (y - 1) = - 4 \\ (x + 1) - (y - 1) = 3 \end{array}$

查看试题解析
19. 解不等式组： ${\begin{array}{l} 3 x - 2 (x + 2) \geq 4 \\ \frac{x - 1}{3} - 1 \leq 2 \end{array}$ ，并写出它的整数解.

查看试题解析
20. 在由边长为 $1$ 个单位长度的小正方形组成的网格中，建立如图所示平面直角坐标系，原点 $O$ 及三角形 $A B C$ 的顶点都在格点上.

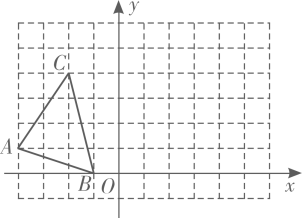(1)、点 $A$ 的坐标为；

(2)、将三角形 $A B C$ 先向右平移 $5$ 个单位长度，再向上平移 $1$ 个单位长度得到三角形 $A_{1} B_{1} C_{1}$ ，画出三角形 $A_{1} B_{1} C_{1}$ ；

(3)、三角形 $A_{1} B_{1} C_{1}$ 的面积为.

查看试题解析
21. 某学校在本学期开展数学拓展活动，为了解开展数学拓展活动后学生不同阶段的学习效果，决定随机抽取七年级部分学生进行两次跟踪测评（两次随机抽取的学生人数相同），第一次是开展数学拓展活动初期的学习质量测评，第二次是开展数学拓展活动 $3$ 个月后的学习质量测评.根据测评的数学成绩制作了第一次测评的数学成绩频数分布直方图（如图，每一组包括左边端点，不包括右边端点）和第二次测评的数学成绩频数分布表（如表）.
第二次测评的数学成绩频数分布表：
成绩
$30 \leq x < 40$
$40 \leq x < 50$
$50 \leq x < 60$
$60 \leq x < 70$
$70 \leq x < 80$
$80 \leq x < 90$
$90 \leq x < 100$
频数
$1$
$2$
$4$
$8$
$15$
$m$
$6$
根据以上图表信息，完成下列问题：
第一次测评的数学成绩频数分布直方图

(1)、 $m =$ ；

(2)、若 $80$ 分及以上为优秀.
①开展数学拓展活动 $3$ 个月后，请估计该校 $700$ 名七年级学生数学成绩优秀的人数；
②请分别计算两次测评数学成绩的优秀率，并对开展数学拓展活动的效果进行分析.

查看试题解析
22. 某加工厂加工 $A$ ， $B$ 两种规格的电线，长度分别为 $3 m$ ， $2 m$ .

(1)、一根长 $20 m$ 的电线，在不造成浪费的前提下，
①要想截成两种规格的电线刚好 $7$ 根，则 $A$ ， $B$ 两种规格的电线应各截几根？
②将电线截成 $A$ ， $B$ 两种规格，你有哪几种截法？

(2)、一根电线长 $300 m$ ，现要截出 $A$ ， $B$ 两种规格的电线共 $125$ 根，且 $A$ 种规格的数量不少于 $B$ 种规格的 $\frac{2}{3}$ ，求 $A$ 种规格的电线应截几根？

查看试题解析
23. 如图，三角形 $A B C$ 中，点 $D$ ， $E$ 分别是 $B C$ ， $A C$ 上的点，且 $D E / / A B$ ， $∠ 1 = ∠ 2$ .

(1)、求证： $E F / / B C$ ；（完成以下填空）
证明： $∵ D E / / A B$ （已知）

$∴ ∠ 2 = ∠ B$ （   ），

又 $∵ ∠ 1 = ∠ 2$ （已知）

$∴ ∠ 1 = ∠ B$ （等量代换），

$∴ E F / / B C$ （  ）.

(2)、 $∠ D E F$ 与 $∠ A C B$ 的平分线交于点 $G$ ， $C G$ 交 $D E$ 于点 $H$ ，
①若 $∠ D E F = 40 °$ ， $∠ A C B = 60 °$ ，则 $∠ G =$   ▲   $°$ ；

②已知 $∠ F E G + ∠ D C G = α$ ，求 $∠ D E C$ .（用含 $α$ 的式子表示）

查看试题解析
24. 【发现问题】已知 ${\begin{array}{l} 3 x + 2 y = 4 ① \\ 2 x - y = 6 ② \end{array}$ ，求 $4 x + 5 y$ 的值.
方法一：先解方程组，得出 $x$ ， $y$ 的值，再代入，求出 $4 x + 5 y$ 的值.

方法二：将① $\times 2 -$ ②，求出 $4 x + 5 y$ 的值.

【提出问题】怎样才能得到方法二呢？

【分析问题】

为了得到方法二，可以将① $\times m +$ ② $\times n$ ，可得 $(3 m + 2 n) x + (2 m - n) y = 4 m + 6 n$ .

令等式左边 $(3 m + 2 n) x + (2 m - n) y = 4 x + 5 y$ ，比较系数可得 ${\begin{array}{l} 3 m + 2 n = 4 \\ 2 m - n = 5 \end{array}$ ，求得 ${\begin{array}{l} m = 2 \\ n = - 1 \end{array}$ .

【解决问题】

(1)、请你选择一种方法，求 $4 x + 5 y$ 的值；

(2)、对于方程组 ${\begin{array}{l} 3 x + 2 y = 4 \\ 2 x - y = 6 \end{array}$ 利用方法二的思路，求 $7 x - 7 y$ 的值；

(3)、【迁移应用】
已知 ${\begin{array}{l} 1 \leq 2 x + y \leq 2 \\ 4 \leq 3 x + 2 y \leq 7 \end{array}$ ，求 $x - 3 y$ 的范围.

查看试题解析

成绩	$30 \leq x < 40$	$40 \leq x < 50$	$50 \leq x < 60$	$60 \leq x < 70$	$70 \leq x < 80$	$80 \leq x < 90$	$90 \leq x < 100$
频数	$1$	$2$	$4$	$8$	$15$	$m$	$6$