四川省乐山市井研县2020-2021学年七年级下学期期末数学试卷
试卷更新日期:2022-06-14 类型:期末考试
一、单选题
-
1. 已知关于x的方程的解是 , 则m的值为( )A、2 B、 C、8 D、102. 已知 , 则的值为( )A、1 B、2 C、3 D、93. 方程 的解是( )A、2 B、﹣3 C、 D、2或﹣34. 下面的图形是用数学家名字命名的,其中是轴对称图形,但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 用正三角形和正六边形铺成一个平面,则在同一个顶点处,正三角形和正六边形的个数之比为( )A、4:1 B、1:1 C、1:4 D、4:1或1:16. 若 ,则下列不等式不一定成立的是( )A、 B、 C、 D、7. 如图, , 其中 , 则的度数为( )
5. 用正三角形和正六边形铺成一个平面,则在同一个顶点处,正三角形和正六边形的个数之比为( )A、4:1 B、1:1 C、1:4 D、4:1或1:16. 若 ,则下列不等式不一定成立的是( )A、 B、 C、 D、7. 如图, , 其中 , 则的度数为( )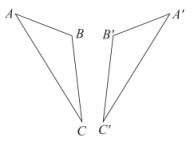 A、 B、 C、 D、8. 如图,七边形 中, 的延长线交于点O,若 , 相邻的外角的和等于 ,则 的度数是( )
A、 B、 C、 D、8. 如图,七边形 中, 的延长线交于点O,若 , 相邻的外角的和等于 ,则 的度数是( ) A、 B、 C、 D、9. 三角形的两边长分别是5和8,则第三边长不可能是( )A、3 B、5 C、7 D、810. 若方程组 的解是 ,则方程组 的解是( )A、 B、 C、 D、11. 若关于x的不等式的解都能使不等式成立,则a的取值范围是( )A、 B、 C、 D、或12. 如图,在中, , 、、分别平分的外角 , 内角 , 外角 , 以下结论:①;②;③;④ , 其中正确的结论有( )
A、 B、 C、 D、9. 三角形的两边长分别是5和8,则第三边长不可能是( )A、3 B、5 C、7 D、810. 若方程组 的解是 ,则方程组 的解是( )A、 B、 C、 D、11. 若关于x的不等式的解都能使不等式成立,则a的取值范围是( )A、 B、 C、 D、或12. 如图,在中, , 、、分别平分的外角 , 内角 , 外角 , 以下结论:①;②;③;④ , 其中正确的结论有( ) A、①②③ B、①③④ C、②③④ D、①②④
A、①②③ B、①③④ C、②③④ D、①②④二、填空题
-
13. 一元一次方程2x=4的解是.14. 不等式5x+8<3(2+x)的解集为 .15. 若将方程变形成用x的代数式表示y,则.16. 若一个多边形的每一个外角都等于 , 则这个多边形的边数为.17. 如图,把周长为12的沿方向平移1个单位得到 , 则四边形的周长为.
 18. 如图,在中, , 是的平分线,是的垂直平分线,则.
18. 如图,在中, , 是的平分线,是的垂直平分线,则. 19. 如图,在中,点D、E、F分别在三边上,E是的中点,、、交于一点G, , , 则的面积是.
19. 如图,在中,点D、E、F分别在三边上,E是的中点,、、交于一点G, , , 则的面积是.
三、解答题
-
20. 定义:对于四位自然数m,若其千位数字与个位数字之和为7,百位数字与十位数字之和也等于7,则称这个四位自然数m为“七巧数”.例如:3254是“七巧数”,因为 , 所以3254是“七巧数”;1456不是“七巧数”,因为 , 所以1456不是“七巧数”.(1)、若一个“七巧数”的千位数字为a,则其个位数字可以表示为;(用含a的代数式表示)(2)、若“七巧数”m的千位数字加上十位数字的和,是百位数字减去个位数字的差的3倍,请写出一个满足条件的“七巧数”.
四、解答题
-
21. 解方程:22. 解方程组:23. 解不等式组: , 并求出它的非负整数解.24. 如图所示,每个小正方形的边长为1,△ABC,△DEF的顶点都在小正方形的顶点处.
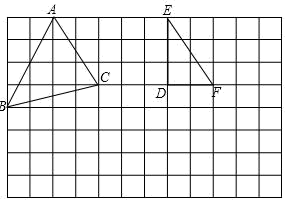 (1)、将△ABC平移,使点A平移到点F,点B,C的对应点分别是点B′,C′,画出△FB′C′;(2)、画出△DEF关于DF所在直线对称的△DE′F;(3)、直接写出四边形B′C′FE′的面积是.25. 如图,在 中,AD是高, ,AE是 外角 的平分线,交BC的延长线于点E,BF平分 交AE于点F,若 ,求 的度数。
(1)、将△ABC平移,使点A平移到点F,点B,C的对应点分别是点B′,C′,画出△FB′C′;(2)、画出△DEF关于DF所在直线对称的△DE′F;(3)、直接写出四边形B′C′FE′的面积是.25. 如图,在 中,AD是高, ,AE是 外角 的平分线,交BC的延长线于点E,BF平分 交AE于点F,若 ,求 的度数。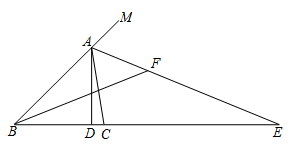 26. 中国民航规定:乘坐飞机商务舱的旅客最多可以免费携带20g的行李,超重部分每千克按照飞机票价格的2%购买行李票.一名乘客携带了的行李从成都乘飞机去北京,结果机票连同行李共付费1440元,则该旅客的飞机票价为多少元?27. 已知关于x、y的方程满足方程组.(1)、若 , 求m的值;(2)、若x、y均为非负数,求m的取值范围,并化简式子;(3)、在(2)问的条件下,求的最大值和最小值.28. 在“抗疫”期间,某药店销售 两种型号的口罩,已知销售600盒 型和400盒 型的利润为8500元,销售300盒 型和450盒 型的利润为6750元.(1)、求每盒 型口罩和每盒 型口罩的销售利润;(2)、该药店计划一次购进 两种型号的口罩共200盒,其中 型口罩的进货量不超过 型口罩的3倍,且完全售出后利润不少于1870元,则该药店共有几种购买方案?请你帮助药店老板设计一种获利最大的进货方案.29. 新定义:对非负实数x“四舍五入”到个位的值记为 , 即:当为非负整数时,如果 , 则;反之,当为非负整数时,如果 , 则.
26. 中国民航规定:乘坐飞机商务舱的旅客最多可以免费携带20g的行李,超重部分每千克按照飞机票价格的2%购买行李票.一名乘客携带了的行李从成都乘飞机去北京,结果机票连同行李共付费1440元,则该旅客的飞机票价为多少元?27. 已知关于x、y的方程满足方程组.(1)、若 , 求m的值;(2)、若x、y均为非负数,求m的取值范围,并化简式子;(3)、在(2)问的条件下,求的最大值和最小值.28. 在“抗疫”期间,某药店销售 两种型号的口罩,已知销售600盒 型和400盒 型的利润为8500元,销售300盒 型和450盒 型的利润为6750元.(1)、求每盒 型口罩和每盒 型口罩的销售利润;(2)、该药店计划一次购进 两种型号的口罩共200盒,其中 型口罩的进货量不超过 型口罩的3倍,且完全售出后利润不少于1870元,则该药店共有几种购买方案?请你帮助药店老板设计一种获利最大的进货方案.29. 新定义:对非负实数x“四舍五入”到个位的值记为 , 即:当为非负整数时,如果 , 则;反之,当为非负整数时,如果 , 则.例如:
试解决下列问题:
(1)、填空:①(为圆周率);②如果 , 则实数x的取值范围为;(2)、若关于的不等式组的整数解恰有3个,求a的取值范围;(3)、求满足的所有非负实数x的值.30. Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α .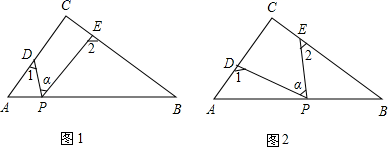
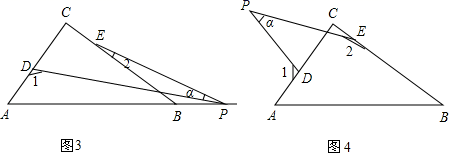 (1)、若点P在线段AB上,如图(1)所示,且∠α=60°,则∠1+∠2=;(2)、若点P在线段AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为;(3)、若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由;(4)、若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.
(1)、若点P在线段AB上,如图(1)所示,且∠α=60°,则∠1+∠2=;(2)、若点P在线段AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为;(3)、若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由;(4)、若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.
-