四川省甘孜藏族自治州2020-2021学年七年级下学期期末数学试卷

试卷更新日期：2022-06-14 类型：期末考试

进入出卷网下载

一、单选题

1. 计算 $2 a \cdot 3 a$ 的结果是（）

A、 $5 a$ B、 $5 a^{2}$ C、 $6 a$ D、 $6 a^{2}$

查看试题解析
2. 下列图案不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，要把河中的水引到村庄A，小凡先作 $A B ⊥ C D$ ，垂足为点B，然后沿 $A B$ 开挖水渠，就能使所开挖的水渠最短，其依据是（）

A、两点确定一条直线 B、两点之间线段最短 C、在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线 D、连结直线外一点与直线上各点的所有线段中，垂线段最短

查看试题解析
4. 下列成语中，表示必然事件的是（）

A、旭日东升 B、守株待兔 C、水中捞月 D、刻舟求剑

查看试题解析
5. 如图，已知直线 $A B$ 、 $C D$ 被直线 $E D$ 所截， $A B / / C D$ ， $∠ 1 = 140 °$ ，则 $∠ D$ 为（）

A、40° B、50° C、60° D、70°

查看试题解析

6. 某电影放映厅周六放映一部电影，当天的场次、售票量、售票收入的变化情况如表所示．在该变化过程中，常量是（　　）

场次	售票量（张）	售票收入（元）
1	50	2000
2	100	4000
3	150	6000
4	150	6000
5	150	6000
6	150	6000

A、场次 B、售票量 C、票价 D、售票收入

查看试题解析

7. 小芳有长度分别为 $4 c m$ 和 $8 c m$ 的两根木条，桌上有下列长度的四根木条，她要用其中的一根与原有的两根木条钉成一个首尾相接的三角形木框，则这根木条的长度为（）

A、 $3 c m$ B、 $5 c m$ C、 $12 c m$ D、 $17 c m$

查看试题解析
8. 如图，用纸板挡住了三角形的一部分，小明根据所学知识很快就画出了一个与原来完全一样的三角形，他的依据是（）

A、ASA B、SAS C、AAS D、SSS

查看试题解析
9. 如图，半圆的直径为AB，圆心为点O，C、D是半圆的3等分点，在该半圆内任取一点，则该点取自阴影部分的概率是（）

A、 $\frac{π}{3}$ B、 $\frac{π}{6}$ C、 $\frac{1}{2}$ D、 $\frac{1}{3}$

查看试题解析
10. “折叠”是数学上常见构造新图形的重要方法如图，矩形ABCD中，点E在边AB上，将矩形ABCD沿图中标示的DE折叠，点A恰好落在边BC的点G处，若∠CDG＝52°，则∠DEG的度数为（）

A、73° B、71° C、68° D、52°

查看试题解析

二、填空题

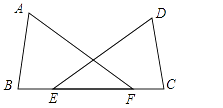
11. ∠α的余角是40°，则∠α＝度.

查看试题解析
12. 冬季流感病毒爆发的高峰期，流行性感冒病简称流感病毒，流感病毒可引起人、禽、猪、马、蝙蝠等多种动物感染和发病，是人流感、禽流感、猪流感、马流感等人与动物疫病的病原，“綦江少年，健康少年”，请綦江少年们注意保暖，多喝热水，开窗通风，防范流感病，以免生病，已知流感病毒的直径为0.00000009米，请将0.00000009米用科学记数法表示为米.

查看试题解析
13. 如图，已知B、E、F、C在同一直线上，BE=CF，AF=DE，则添加条件，可以判断△ABF≌△DCE．

查看试题解析

14. 某商场设立了一个可以自由转动的转盘，并规定：顾客购物30元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据：

转动转盘的次数	100	200	300	500	1000
落在“签字笔”区域的次数	65	122	190	306	601

假如你去转动该转盘一次.你获得签字笔的概率约是.（精确到0.1）

查看试题解析

15. 若计算 $(y + n) (4 y - 3) - 5 y$ 所得的结果中不含y的一次项，则常数n的值为.

查看试题解析
16. 学校举办庆元旦智力竞赛，竞赛的记分方法是：开始前，每位参赛者都有100分作为底分，竞赛中每答对一个问题加10分，答错或不答得0分.代表某班参赛的小亮答对问题为 $x$ 个，小亮的竞赛总得分为 $y$ （分），那么 $y$ 与 $x$ 之间的关系式为.

查看试题解析
17. 如果从1，2，3，4，5，6，7，8，9，10这10个数中任意选取一个数，那么取到的数恰好是5的倍数的概率是．

查看试题解析
18. 如图，3×3方格图中，将其中一个小方格的中心画上半径相等的圆，使整个图形为轴对称图形，这样的轴对称图形共有个。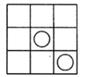

查看试题解析
19. 如图所示，第1个图中有1个三角形，第2个图中共有5个三角形，第3个图中共有9个三角形，依此类推，则第6个图中共有三角形个.

查看试题解析

三、解答题

20.

(1)、计算： $3^{2} - | - 8 | + {(π - 2016)}^{0} - {(- \frac{1}{2})}^{- 1}$ ；

(2)、先化简，再求值. $[{(x + 2 y)}^{2} - (x + y) (3 x - y) - 5 y^{2}] \div 2 x$ ，其中 $x = - 2$ ， $y = \frac{1}{2}$ .

查看试题解析
21. 按逻辑填写步骤和理由：如图， $a$ ∥ $b$ ，点 $A$ 在直线 $a$ 上，点 $B$ 、 $C$ 在直线 $b$ 上，且 $B A ⊥ C A$ ，点 $D$ 在线段 $B C$ 上，连接 $A D$ ，且 $A C$ 平分 $∠ D A F$ .请证明： $∠ 3 = ∠ 5$ .
证明：∵ $B A ⊥ C A$ （已知）
∴ $∠ B A C = ∠ 2 + ∠ 3 = 90 °$ （   ）
∵ $∠ 1 + ∠ B A C + ∠ 4 = 180 °$ （平角的定义）
∴ $∠ 1 + ∠ 4 = 180 ° - ∠ B A C = 180 ° - 90 ° = 90 °$
∵ $A C$ 平分 $∠ D A F$ （已知）
∴ $∠ 1 =$   ▲  （  ）
∴ $∠ 3 = ∠ 4$ （  ）
∵ $a$ ∥ $b$ （已知）
∴ $∠ 4 = ∠ 5$ （  ）
∴ $∠ 3 = ∠ 5$ （  ）

查看试题解析
22. 在 $Δ A B C$ 中，已知 $A B = 3, A C = 7$ ，若第三边 $B C$ 的长为偶数，求 $Δ A B C$ 的周长.

查看试题解析
23. 如图是一位病人的体温记录图，看图回答下列问题：

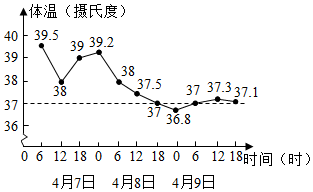(1)、自变量是，因变量是；

(2)、护士每隔小时给病人量一次体温；

(3)、这位病人的最高体温是摄氏度，最低体温是摄氏度；

(4)、他在4月8日12时的体温是摄氏度；

(5)、图中的横虚线表示的含义.

查看试题解析
24. 如图，△ABC中，∠ABC＝25°，∠ACB＝55°，DE，FG分别为AB，AC的垂直平分线，E，G分别为垂足；

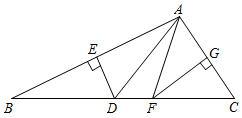(1)、直接写出∠BAC的度数；

(2)、求∠DAF的度数；

(3)、若BC的长为30，求△DAF的周长.

查看试题解析
25. 如图，在 $△ A B C$ 中， $A B = A C$ ，点 $D$ 在 $B C$ 边上，点 $E$ 在 $A C$ 边上，连接 $A D$ ， $D E$ .已知 $∠ 1 = ∠ 2$ ， $A D = D E$ .

(1)、 $△ A B D$ 与 $△ D C E$ 全等吗？为什么？

(2)、若 $B D = 2$ ， $C D = 5$ ，求 $A E$ 的长.

查看试题解析
26. 手机微信中的抢红包游戏有一种玩法为“拼手气红包”：用户设定好总金额以及红包个数之后，可以生成不等金额的红包，现有四个人组成的微信群中，其中一人发了三个“拼手气红包”，其他三人随机抢红包.

(1)、若甲的速度最快，求甲抢到最多金额的红包的概率.

(2)、若三个人同时点击红包，记金额最多、居中、最少的红包分别为A、 $B$ 、C，试求出甲抢到红包A的概率P（A）.

查看试题解析
27. 如图1是一个长为 $4 a$ ，宽为 $b$ 的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成如图2的正方形.

(1)、图2中的阴影正方形边长表示正确的序号为；
① $a + b$ ；② $b - a$ ；③ $(a + b) (b - a)$ .

(2)、由图2可以直接写出 ${(a + b)}^{2}$ ， ${(b - a)}^{2}$ ， $a b$ 之间的一个等量关系是；

(3)、根据（2）中的结论，解决下列问题： $x + y = 8$ ， $x y = 2$ ，求 ${(x - y)}^{2}$ 的值.

查看试题解析
28. 小明和小华是姐弟俩，某日早晨，小明7：40先从家出发去学校，走了一段后，在途中广场看到志愿者们在向过往行人讲解卫生防疫常识，小明想起自己在学校学到的卫生防疫常识，于是停下来加入了志愿者队伍，后来发现上课时间快到了，就开始跑步上学，恰好在8：00赶到学校；小华离家后沿着与小明同一条道路前往学校，速度一直保持不变，也恰好在8：00赶到学校，他们从家到学校已走的路程 $s$ （米）和所用时间 $t$ （分钟）的关系图如图所示，请结合图中信息解答下列问题：

(1)、小明家和学校的距离是米；小明在广场向行人讲解卫生防疫常识所用的时间是分钟；

(2)、分别求小华的速度和小明从广场跑去学校的速度；

(3)、求小华在广场看到小明时是几点几分？

(4)、如果小明在广场进行卫生防疫常识讲解后，继续以之前的速度去往学校，假设讲解1次卫生防疫常识需要1分钟，在保证不迟到（不超过8：00）的情况下，通过计算求小明最多可以讲解几次？（结果保留整数）

查看试题解析