四川省达州市开江县2020-2021学年七年级下学期期末数学试题
试卷更新日期：2022-06-14 类型：期末考试
一、单选题
-
1. 下面有4个汽车标致图案，其中不是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列计算正确的是（ ）A、x3－x2＝x B、x2·x 3＝x6 C、x6÷x3＝x2 D、（x3）2＝x63. 下列算式能用平方差公式计算的是（ ）A、（x﹣2）（x+3） B、（x+y）（y﹣x） C、（2x+y）（﹣2x﹣y） D、（﹣x+1）（x﹣1）4. 已知 ， 则的值是（ ）A、4 B、8 C、12 D、165. 下列事件为不可能事件的是（ ）A、太阳从西边升起 B、买一张电影票，座位号是奇数号 C、任意画一个三角形，其内角和是180° D、同位角相等6. 空气的密度是0.00012g/cm3 ， 将数据0.00012用科学记数法表示为（ ）A、0.12×10﹣3 B、0.12×10﹣7 C、1.2×10﹣4 D、1.2×10﹣67. 今年端午期间，小丽同学从家里出发骑单车去公园，途中，她在路边的便利店挑选一瓶矿泉水，耽误了一段时间后继续骑行，愉快地到了公园.图中描述了小丽路上的情景，下列说法中错误的是（ ）
A、小丽在便利店时间为10分钟 B、便利店离小丽家的距离为1000米 C、小丽从家到达公园共用时间20分钟 D、小丽后面骑行速度比前面快8. 如图，l1∥l2∥l3 ， ∠1＝60°，∠2＝20°，∠3的度数是（ ）
A、120° B、140° C、110° D、130°9. 如图，在四边形ABCD中，∠A＝∠C＝90°，∠B＝32°，在边AB，BC上分别找一点E，F使△DEF的周长最小，此时∠EDF＝（ ）
A、110° B、112° C、114° D、116°10. 如图，Rt△ACB中，∠ACB＝90°，△ABC的角平分线AD、BE相交于点P，过P作PF⊥AD交BC的延长线于点F，交AC于点H，则下列结论：①∠APB＝135°；②BF＝BA；③PH＝PD；④连接CP，CP平分∠ACB，其中正确的是（ ）
A、①②③ B、①②④ C、①③④ D、①②③④二、填空题
-
11. 已知am＝4，an＝5，则am+2n的值是 .12. 有九张相同的卡片，上印有汉字“爱祖国爱人民爱劳动”.九张卡片任意搅乱后，一个人随机抽取一张，卡片上写有汉字“爱”的概率是 .13. 当三角形中的一个内角α是另一个内角β的二倍时，我们称此三角形为“特征三角形”，其中α称为“特征角”.如果一个“特征三角形”有一个角是60°三角形，则这个三角形的其他两个角的度数为 .14. 若代数式x2+4x+6可以表示为（x+1）2+a（x+1）+3的形式，则a＝.15. 如图，在△ABC中，∠ACB＝90°，AC＝BC，过点A，B分别作过点C的直线的垂线AE，BF.若AE＝2，BF＝4，则EF＝.
16. 如图，点C为线段AB的中点，以BC为边作正方形BCDE，点F、点G分别在边DE、DC上，且满足DF＝DG，连接BF，连接AG并延长交BF于点H，连接DH．以下结论：① ACG≌ BEF；②HD＝HG；③AH⊥BF；④∠DHG＝45°．其中正确的有（填序号）．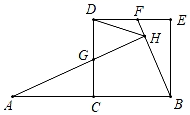
三、解答题
-
17.(1)、计算：|﹣1|+（π﹣3.14）0﹣+（﹣1）2021；(2)、20222﹣4040×2022+20202.18. 先化简，再求值： ，其中 ， .19. 如图，在长度为1个单位长度的小正方形组成的正方形网格中，△ABC的三个顶点A、B、C都在格点上.
(1)、在图中画出与△ABC关于直线L成轴对称的△A′B′C′；(2)、求△ABC的面积.(3)、在直线L上找出一点P，使得PA+PC的值最小.（在图上直接标记出点P的位置）20. 2021年6月14日是第18个世界献血者日，我县将采取自愿报名的方式组织市民义务献血.献血时要对献血者的血型进行检测，检测结果有“A型”，“B型”，“AB型”，“O型”4种类型.在献血者人群中，随机抽取了部分献血者的血型结果进行统计，并根据这个统计结果制作了两幅不完整的图表.血型
A
B
AB
O
人数
x
40
20
y
(1)、这次随机抽收的献血者人数为人，m＝；(2)、求x，y的值；(3)、请你根据抽样结果回答：从献血者人群中任抽取一人.其血型是O型的概率是多少？若这次活动中有10000人义务献血，大约有多少人是O型血？21. 甲骑车从A地到B地，乙骑车从B地到A地，甲的速度小于乙的速度，两人同时出发，沿同一条道骑行，图中的折线表示两人之间的距离y（km）与甲的行驶时间x（h）之间的关系，根据图象回答下列问题：
(1)、A地B地两点的距离是km；C点的实际意义；(2)、求甲、乙相遇的时间；(3)、求甲出发多长时间两人相距10千米.22. 如图，已知 .
(1)、若 求 的度数；(2)、求证： .23.(1)、已知：a（a+1）﹣（a2+b）＝3，a（a+b）+b（b﹣a）＝15，求代数式ab的值；(2)、已知a，b，c是△ABC的三边，其中a，b满足a2+b2＝6a+14b﹣58，c满足|5﹣c|＝1，求△ABC的周长.24. 观察下列各式：13+23＝1+8＝9，而（1+2）2＝9，∴13+23＝（1+2）2；
13+23+33＝36，而（1+2+3）2＝36，∴13+23+33＝（1+2+3）2；
13+23+33+43＝100，而（1+2+3+4）2＝100，∴13+23+33+43＝（1+2+3+4）2；
(1)、猜想并填空：13+23+33+43+53＝2＝2；(2)、根据以上规律填空：13+23+33+…+n3＝2＝2；(3)、求解：163+173+183+193+203.25.
(1)、基础应用：如图1，在△ABC中，AB＝5，AC＝7，AD是BC边上的中线，延长AD到点E使DE＝AD，连接CE，把AB，AC，2AD利用旋转全等的方式集中在△ACE中，利用三角形三边关系可得AD的取值范围是；(2)、推广应用：应用旋转全等的方式解决问题如图2，在△ABC中，AD是BC边上的中线，点E，F分别在AB，AC上，且DE⊥DF，求证：BE+CF＞EF；(3)、综合应用：如图3，在四边形ABCD中，AB＝AD，∠B+∠ADC＝180°且∠EAF＝∠BAD，试问线段EF、BE、FD具有怎样的数量关系，并证明.