四川省成都市成华区2020-2021学年七年级下学期期末数学试卷
试卷更新日期：2022-06-14 类型：期末考试
一、单选题
-
1. 汽车以每小时100千米的速度匀速行驶，行驶的路程随时间的变化而变化，在这个变化过程中，自变量是（ ）A、汽车 B、路程 C、速度 D、时间2. 下列四个图形中，不是轴对称图形的是（ ）A、
B、
C、
D、
3. 肥皂泡的泡壁厚度大约是0.00000071米，数字0.00000071用科学记数法表示为（ ）A、7.1×10﹣9 B、7.1×10﹣8 C、7.1×10﹣7 D、7.1×10﹣64. 下列计算正确的是（ ）A、（a2）4＝a8 B、a2•a4＝a8 C、（a+b）2＝a2+b2 D、a2+a2＝a45. 下列事件中，不是必然事件的是（ ）A、等角的余角相等 B、对顶角相等 C、垂线段最短 D、同位角相等6. 等腰三角形的两条边长分别为3和7，则这个等腰三角形的周长是（ ）A、10 B、13 C、17 D、13或177. 若关于x的二次三项式x2+ax+4是完全平方式，则a的值是（ ）A、4 B、2 C、±4 D、±28. 如图，在△ABC和△ABD中，∠CAB＝∠DAB，点A，B，E在同一条直线上，则添加以下条件，仍然不能判定△ABC≌△ABD的是（ ）
A、BC＝BD B、∠C＝∠D C、∠CBE＝∠DBE D、AC＝AD9. 如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，若BC=6，AC=5，则△ACE的周长为（ ）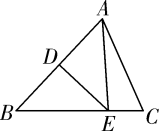
A、8 B、11 C、16 D、1710. 已知点P为某个封闭图形边界上的一定点，动点M从点P出发，沿其边界顺时针匀速运动一周，设点M的运动时间为x，线段PM的长度为y，表示y与x的函数图象大致如图所示，则该封闭图形可能是（ ）
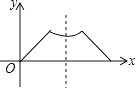A、
B、
C、
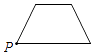D、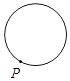
二、填空题
-
11. 计算： ．12. 从﹣1，0，2和3中随机地选一个数，则选到正数的概率是 .13. 如图，AB∥CD，点P在CD上，PF平分∠EPC，∠1＝55°，则∠EPD＝.
14. 如图，△ABC中，AC＝BC，点D，E，F分别在边AC，AB，BC上，且满足AD＝BE，AE＝BF，∠DEF＝40°，则∠C的度数是 .
15. 若a+b＝3，a2+b2＝7，则ab＝ ．16. 从长度分别为1cm，3cm，5cm，6cm的四条线段中随机取出三条，则能够成三角形的概率为 .17. 请按如图方法操作：①对折长方形纸片ABCD，使AD与BC重合，得到折痕EF；②把纸片展平，在BC上取点M，沿AM再次折叠纸片，并使点B落在EF上的点B′处；③把纸片展平，连接AB′.则∠AB′E的度数是 .
18. 甲、乙两人在笔直的健身步道上同起点、同终点、同方向匀速步行2400米，先到终点的人原地休息.已知甲先出发4分钟，在整个步行过程中，甲、乙两人的距离y（米）与甲出发的时间t（分）之间的关系如图所示，则甲、乙两人距离的最大值是 米.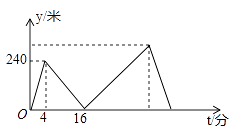
19. 如图，∠AOB30°，点P是∠AOB内的一定点，且OP6，若点M，N分别是射线OA，OB上异于点O的动点，则△PMN周长的最小值是.
三、解答题
-
20. 计算：(1)、；(2)、[（x+1）（x+2）+2（x﹣1）]÷x.21.(1)、先化简，再求值：（2x+3）（2x﹣3）﹣（x+2）2+4（x+3），其中x＝﹣2；(2)、先化简，再求值：（x﹣2y）2﹣（x﹣2y）（2x+y）+（x﹣y）（x+y），其中x＝5y.22. 如图，AB∥CD，AB＝CD，点E，F在BC上，且BE＝CF.
求证：
(1)、AF＝DE；(2)、AF∥DE.23. 某健身俱乐部每次健身费用为25元.暑期来临之际，该俱乐部面向学生推出了两种暑期优惠方案，方案一：购买一张50元的学生暑期专享卡，每次健身费用按六折优惠；方案二：不购买学生暑期专享卡，每次健身费用按八折优惠.设某学生暑期健身x次，按照方案一所需费用为y1（元），按照方案二所需费用为y2（元）.(1)、分别写出y1和y2与x的关系式；(2)、小明同学计划暑期前往该俱乐部健身9次，通过计算说明选择哪种方案费用少？24. 某商场根据第二季度某品牌运动服装的S号、M号、L号、XL号、XXL号销售情况绘制了如图所示的不完整的两幅统计图.根据图中信息解答下列问题：
(1)、第二季度该品牌运动服装的销售总量是件，扇形统计图中XXL号服装销量占总量的百分比是 ， XL号所对应的圆心角度数是；(2)、请补全条形统计图；(3)、从M号、XL号运动服装中按照M号，XL号运动服装的销量比，分别取出一定数量的运动服，再取3件XXL号运动服装，将它们放在一起，现从这些运动服装中，随机取出1件，取得M号运动服装的概率为 ， 求取出了M号、XL号运动服装各多少件？25. 如图，点P，Q分别是等边△ABC边AB，BC上的动点（端点除外），点P从点A出发，沿AB向点B方向运动，同时，点Q从点B出发，以相同的速度沿BC向点C方向运动.连接AQ，CP，AQ，CP交于点M.
(1)、求证：AQ＝CP；(2)、求∠QMC的度数；(3)、若点P，Q分别运动到AB，BC的延长线上，直线AQ，CP交于点M，请在备用图中补全图形，并求出∠QMC的度数.26. 若a，b，c为 的三边．(1)、化简：|a﹣b+c|+|c﹣a﹣b|﹣|a+b|；(2)、若a，b，c都是正整数，且a2+b2﹣2a﹣8b+17＝0， 的周长．27. 在一条笔直的公路上依次有A，C，B三地，甲、乙两人同时出发，甲从A地骑自行车去B地，途经C地休息1分钟，继续按原速骑行至B地，甲到达B地后，立即按原路原速返回A地；乙步行从B地前往A地．甲、乙两人距A地的路程y（米）与时间x（分）之间的函数关系如图所示，请结合图象解答下列问题：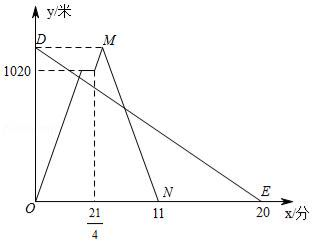
(1)、请写出甲的骑行速度为米/分，点M的坐标为；(2)、求甲返回时距A地的路程y与时间x之间的函数关系式（不需要写出自变量的取值范围）；(3)、请直接写出两人出发后，在甲返回A地之前，经过多长时间两人距C地的路程相等．28. 如图，在边长为8的正方形ABCD中，点E在边AB上移动（不与端点重合）.连接CE，以CE为一边在其右侧作△CEF，其中∠CEF＝90°，CE＝EF，点G为FC的中点，过点F作FH⊥AD，垂足为点H，连接GD，GH，FA.
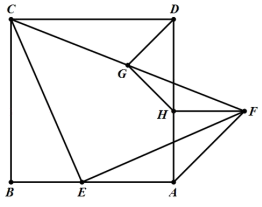(1)、求证：∠EAF＝135°；(2)、请判断线段GD和GH之间有何关系？写出你的结论并证明；(3)、在点E移动过程中，△EAF的面积有最大值吗？如果有，求出△EAF面积的最大值及此时BE的长；如果没有，说明理由.