四川省成都市东部新区2021-2022学年高二下学期理数期中考试试卷
试卷更新日期:2022-06-13 类型:期中考试
一、单选题
-
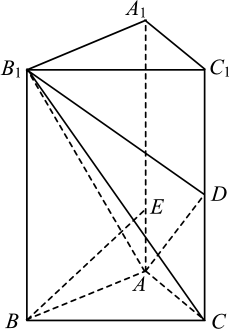
1. 函数在区间上的平均变化率为( )A、-4 B、4 C、-6 D、62. 已知i是虚数单位,则复数的虚部是( )A、1 B、 C、-1 D、3. 在空间直角坐标系中,已知 , , 则MN的中点P到坐标原点О的距离为( )A、 B、 C、2 D、34. 若直线l的方向向量 , 平面的法向量 , 则( )A、 B、 C、 D、或5. 已知 , 则( )A、 B、 C、 D、6. 若是函数的极值点,则的值是( )A、-1 B、0 C、1 D、e7. 已知在上单调递增,则实数a的取值范围为( )A、 B、 C、 D、8. 如图所示,在平行六面体中,M为与的交点,若 , , , 则( )
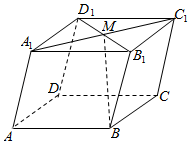 A、 B、 C、 D、9. 在长方体 中, , ,则异面直线 与 所成角的余弦值为( )A、 B、 C、 D、10. 已知函数 , 则方程实根的个数为( )A、2 B、3 C、4 D、511. 已知是定义在上的函数,且 , 导函数满足恒成立,则不等式的解集为( )A、 B、 C、 D、12. 在平面向量中,我们用表示在方向上的投影,换个角度,向量在直线OB的法向量方向上的投影的绝对值就是点A到直线OB的距离(如图1),如果利用类比的方法,那么图2中点A到平面BCD的距离为( )
A、 B、 C、 D、9. 在长方体 中, , ,则异面直线 与 所成角的余弦值为( )A、 B、 C、 D、10. 已知函数 , 则方程实根的个数为( )A、2 B、3 C、4 D、511. 已知是定义在上的函数,且 , 导函数满足恒成立,则不等式的解集为( )A、 B、 C、 D、12. 在平面向量中,我们用表示在方向上的投影,换个角度,向量在直线OB的法向量方向上的投影的绝对值就是点A到直线OB的距离(如图1),如果利用类比的方法,那么图2中点A到平面BCD的距离为( )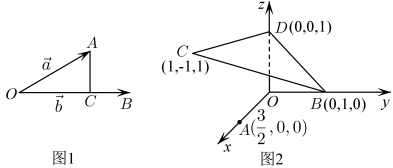 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. = .14. 已知复数 满足 ( 是虚数单位),则 .15. 已知向量 , , 若与互相垂直,则.16. 已知是函数的切线,则的最小值为.
三、解答题
-
17. 设数列满足 , .(1)、求 , , , 并猜想数列的通项公式;(2)、用数学归纳法证明(1)中的猜想.18. 已知函数 , 曲线在处的切线方程为.(1)、求的值;(2)、求在区间上的最值.19. 已知空间三点 , , .(1)、求以AB,AC为邻边的平行四边形的面积;(2)、设 , 若A,B,C,D四点共面,求的值