陕西省咸阳市武功县2021-2022学年高二下学期理数期中考试试卷

试卷更新日期：2022-06-13 类型：期中考试

进入出卷网下载

一、单选题

1. 设复数z满足 $z + 1 - 2 i = - 3 + i ，$ ，则 $| z | =$ （）

A、6 B、6 $\sqrt{2}$ C、 $5 \sqrt{2}$ D、5

查看试题解析
2. 已知函数 $f (x)$ 在 $x = x_{0}$ 处的导数为 $- 2$ ，则 $\underset{k \to 0}{l i m} \frac{f (x_{0} + k) - f (x_{0})}{k}$ 等于（）

A、－2 B、－1 C、2 D、1

查看试题解析
3. 设i是虚数单位， $\bar{z}$ 是复数z的共轭复数，若 $z = 2 - i$ ，则 $z + i \bar{z}$ 在复平面内对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 一质点在单位圆上作圆周运动，其位移满足的方程为 $h = s i n 2 t$ ，其中h表示位移（单位：m），t表示时间（单位：s），则该质点在 $t = 3 s$ 时的瞬时速度为（）

A、 $2 s i n 6 m / s$ B、 $2 c o s 6 m / s$ C、 $s i n 6 m / s$ D、 $c o s 6 m / s$

查看试题解析
5. 用反证法证明“在同一平面内，若 $a ⊥ c$ ， $b ⊥ c$ ，则 $a / / b$ 时”应假设（）

A、 $a$ 不垂直于 $c$ B、 $a$ ， $b$ 都不垂直于 $c$ C、 $\vec{a} ⊥ \vec{b}$ D、 $a$ 与 $b$ 不平行

查看试题解析
6. 已知函数 $f (x)$ 的导函数的图象如图所示，则 $f (x)$ 的极值点的个数为（）

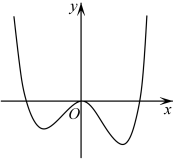A、0 B、1 C、2 D、3

查看试题解析
7. 某箱子的容积V与底面边长x的关系为 $V (x) = \frac{1}{2} x^{2} (60 - x) (0 < x < 60)$ ，则当箱子的容积最大时，箱子的底面边长为（）

A、30 B、40 C、50 D、55

查看试题解析
8. 为贯彻教育部关于全面推进素质教育的精神，某学校推行体育选修课，甲、乙、丙、丁四人分别从太极拳、足球、击剑、游泳四门课程中选择一门课程作为选修课，他们分别有以下要求：
甲：我不选太极拳和足球；
乙：我不选太极拳和游泳；
丙：我的要求和乙一样；
丁：如果乙不选足球，我就不选太极拳．
已知每门课程都有人选择，且都满足四个人的要求，据此推断选击剑的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
9. 已知 $a = \frac{l n 3}{3}$ ， $b = \frac{1}{e}$ ， $c = \frac{l n 5}{5}$ ，则以下不等式正确的是（）

A、 $c > b > a$ B、 $a > b > c$ C、 $b > a > c$ D、 $b > c > a$

查看试题解析
10. 已知 $x = 2$ 是函数 $f (x) = e^{x} + m x$ 的极值点，若关于 $x$ 的方程 $f (x) = k$ 在 $(- 1 ， + \infty)$ 上有两个不同的实根，则实数 $k$ 的取值范围是（）

A、 $(- e^{2} ， \frac{1}{e} + e^{2})$ B、 $(- e^{2} ， + \infty)$ C、 $(- e^{2} ， \frac{1}{e} + e^{2}]$ D、 $(\frac{1}{e} + e^{2} ， + \infty)$

查看试题解析
11. 已知关于x的不等式 $x + e^{x} (x - \frac{1}{2} x^{2} - a) \geq 0$ 有解，则实数a的取值范围为（）

A、 $[\frac{1}{e} + \frac{1}{2} ， + ∞)$ B、 $(- ∞ ， 0)$ C、 $(- \infty ， 1)$ D、 $(- ∞ ， \frac{1}{e} + \frac{1}{2}]$

查看试题解析
12. 连续函数 $f (x)$ 是定义在 $(- 1 ， 1)$ 上的偶函数，当 $x \neq 0$ 时， $x f^{'} (x) > 0$ .若 $f (a + 1) - f (2 a) > 0$ ，则 $a$ 的取值范围是（）

A、 $(- \frac{1}{3} ， 1)$ B、 $(- \frac{1}{2} ， 0)$ C、 $(- \frac{1}{2} ， 1)$ D、 $(- \frac{1}{3} ， 0)$

查看试题解析

二、填空题

13. 设函数 $f (x)$ 的导函数为 $f^{'} (x)$ ，已知函数 $f (x) = 2 f^{'} (1) x - x^{2}$ ，则 $f^{'} (1) =$ ．

查看试题解析
14. 若复数z满足 $(2 - i) z = i^{2022}$ ，则 $z =$ ．

查看试题解析
15. 已知函数 $y = f (x)$ 的图象过原点，且 $y = f (x)$ 在原点的切线为第一、三象限的平分线，试写出一个满足条件的函数.

查看试题解析
16. 若定义在区间D上的函数 $f (x)$ 的导函数为增函数，则 $f (x)$ 为D上的凹函数．下列四个函数中为 $(0 ， + ∞)$ 上的凹函数的是．（填序号）
① $f (x) = x^{3} - x^{2}$ ；② $f (x) = x - l n x$ ；③ $f (x) = x - e^{x}$ ；④ $f (x) = \frac{x + 1}{x}$ ．

查看试题解析

三、解答题

17. 求下列函数的导数：

(1)、 $y = \sqrt{x} l n x$ ；

(2)、 $y = s i n (x + 1) - c o s \frac{x}{2}$ ．

查看试题解析
18. 已知复数 $z = m^{2} - 2 m - 15 + (m^{2} - 9) i$ ，其中 $m \in R$ ， i为虚数单位．

(1)、若z为实数，求m的值；

(2)、若z为纯虚数，求 $\frac{z}{1 + i}$ 的虚部．

查看试题解析
19. 已知函数 $f (x) = x^{3} - 3 a x + 2$ ，曲线 $y = f (x)$ 在 $x = 1$ 处的切线方程为 $3 x + y + m = 0$ .
（Ⅰ）求实数 $a$ ， $m$ 的值；

（Ⅱ）求 $f (x)$ 在区间 $[1 ， 2]$ 上的最值.

查看试题解析
20. 记 $S_{n}$ 为等差数列 ${a_{n}}$ 的前 $n$ 项和，且 $S_{4} = 20$ ， $a_{5} = 10$ .

(1)、求 $S_{n}$ ；

(2)、用数学归纳法证明： $\sqrt{S_{1}} + \sqrt{S_{2}} + \sqrt{S_{3}} + ⋯ + \sqrt{S_{n}} > \frac{n (n + 1)}{2} (n \in N_{+})$ .

查看试题解析
21. 已知函数 $f (x) = \frac{e^{x}}{x} - a (x - l n x) + a$ （a为实数）．

(1)、当 $a = - 1$ 时，求函数 $f (x)$ 的单调区间；

(2)、若函数 $f (x)$ 在（0，1）内存在唯一极值点，求实数a的取值范围．

查看试题解析
22. 已知函数 $f (x) = \frac{1}{2} e^{2 x} + (1 - a) e^{x} - a x - \frac{1}{2} a^{2}$ ．

(1)、讨论函数 $f (x)$ 的单调性；

(2)、当 $x \in R$ 时，若 $f (x) > 0$ 恒成立，求实数a的取值范围．

查看试题解析