广西梧州市岑溪市2021-2022学年高二下学期理数期中考试试卷

试卷更新日期：2022-06-13 类型：期中考试

进入出卷网下载

一、单选题

1. 若集合M＝{－1，0，1}，集合N＝{0，1，2}，则M∪N＝（）

A、{0，1} B、{－1，0，1} C、{0，1，2} D、{－1，0，1，2}

查看试题解析
2. $i + \frac{1}{i} =$ （）

A、0 B、 $2 i$ C、 $- 2 i$ D、 $- 1 + i$

查看试题解析
3. 已知向量 $\vec{a}$ ， $\vec{b}$ ， “ $\vec{a} \cdot \vec{b} = 0$ ”是“ $\vec{a} = \vec{0}$ 或 $\vec{b} = \vec{0}$ ”的（）条件.

A、充分不必要 B、必要不充分 C、充分必要 D、既不充分也不必要

查看试题解析
4. 下列区间中，函数 $f (x) = 2 s i n (x + \frac{π}{3})$ 单调递增的是（）

A、 $(0 ， \frac{π}{6})$ B、 $(\frac{π}{6} ， \frac{π}{2})$ C、 $(\frac{π}{2} ， \frac{2 π}{3})$ D、 $(\frac{π}{3} ， \frac{π}{2})$

查看试题解析
5. 设实数x，y满足 ${\begin{array}{l} 3 x + y - 6 \geq 0 \\ x - y + 1 \geq 0 \\ x - 2 y - 2 \leq 0 \end{array}$ ，则 $z = 2 x + y$ 的最小值为（）

A、 $\frac{23}{4}$ B、-2 C、4 D、2

查看试题解析
6. 双曲线 $C ： \frac{y^{2}}{a^{2}} - \frac{x^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的一条渐近线的倾斜角为60°，则C的离心率为（）

A、2 B、 $\sqrt{2}$ C、3 D、 $\frac{2 \sqrt{2}}{3}$

查看试题解析
7. 已知函数 $f (x)$ 为R上的奇函数，当 $x < 0$ 时， $f (x) = x + 2$ ，则 $f (0) + f (3)$ 等于（）

A、-3 B、-1 C、1 D、3

查看试题解析
8. 如图，在正方体 $A_{1} B_{1} C_{1} D_{1} - A B C D$ 中， $P$ 为 $C_{1} D_{1}$ 的中点，则过点 $A_{1}$ ， $B$ ， $P$ 的平面截正方体所得的截面的侧视图（阴影部分）为（）

A、 B、 C、 D、

查看试题解析
9. 已知半径为2的圆经过点 $(2 ， 1)$ ，则其圆心到原点的距离的最小值为（）

A、 $\sqrt{5} + 2$ B、 $\sqrt{5} - 2$ C、 $\sqrt{5}$ D、3

查看试题解析
10. 已知 $A ， B$ 为球 $O$ 的球面上两点，过弦 $A B$ 的平面截球 $O$ 所得截面面积的最小值为 $9 π$ ，且 $△ O A B$ 为等边三角形，则球 $O$ 的表面积为（）

A、36π B、54π C、108π D、144π

查看试题解析
11. 已知随机变量X，Y分别满足 $X ∼ B (8 ， p)$ ， $Y ∼ N (μ ， σ^{2})$ ，且期望 $E (X) = E (Y)$ ，又 $P (Y \geq 4) = \frac{1}{2}$ ，则 $p =$ （）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{3}{8}$ D、 $\frac{1}{2}$

查看试题解析
12. 已知整数数列 ${b_{n}}$ 满足 $4^{n} - \frac{1}{7} < b_{n + 1} - b_{n - 1} < 4^{n} + \frac{1}{7}$ ， $b_{2} = 4$ ，则 $b_{2022} =$ （）

A、 $\frac{2^{2022} - 64}{3}$ B、 $\frac{4^{2023} - 4}{15}$ C、 $\frac{2^{1018} - 37}{3}$ D、 $\frac{4^{2022} - 56}{15}$

查看试题解析

二、填空题

13. 已知曲线 $f (x) = x + 2^{x}$ ，则曲线 $f (x)$ 在点 $(1 ， f (1))$ 处的切线方程为.

查看试题解析
14. ${(\sqrt{x} - \frac{2}{x})}^{5}$ 的展开式中x的系数为（用数字作答）.

查看试题解析
15. 若 $t a n α = l g (10 a)$ ， $t a n β = l g \frac{1}{a}$ ，且 $α + β = \frac{π}{4}$ ，则实数 $a$ 的值为．

查看试题解析
16. 已知点 $A (0 ， 2)$ ，抛物线 $y^{2} = 2 p x (p > 0)$ 的焦点为 $F$ ，准线为 $l$ ，线段 $F A$ 交抛物线于点 $B$ ，过点 $B$ 作准线 $l$ 的垂线，垂足为 $M$ .若 $A M ⊥ M F$ ，则 $p =$ .

查看试题解析

三、解答题

17. 已知等差数列{ $a_{n}$ }的前n项和为 $S_{n}$ ， $a_{2} + a_{3} = 7 ， S_{5} = 15$ ．

(1)、求等差数列{ $a_{n}$ }的通项公式；

(2)、若 $b_{n} = 2^{a_{2 n}}$ ，求 $b_{1} + b_{2} + b_{3} + ⋯ + b_{n}$ 的值．

查看试题解析
18. 已知锐角 $△ A B C$ 的内角A，B，C的对边分别为a，b，c，且 $(2 b - c) c o s A = a c o s C$ .

(1)、求A；

(2)、若 $a = 2$ ， $△ A B C$ 的周长为6，求 $△ A B C$ 的面积.

查看试题解析
19. “冰雪为媒，共赴冬奥之约”！第24届冬季奥林匹克运动会于2022年2月4日于20日在北京举行，共有91个国家的代表团参加.各国运动员在赛场上全力以赴、奋勇争先，为我们带来了一场冰与雪的视觉盛宴.本届奥运会前，为了分析各参赛国实力与国家所在地区（欧洲/其它）之间的关系，某体育爱好者统计了近年相关冰雪运动赛事（奥运会、世锦寒等）中一些国家斩获金牌的次数，得到如下茎叶图.

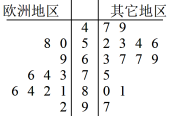(1)、计算并比较茎叶图中“欧洲地区”国家和“其它地区”国家获金牌的平均次数（记为 $\bar{x_{1}} 、 \bar{x_{2}}$ ）和方差（记为 $s_{1}^{2} 、 s_{2}^{2}$ ，保留一位小数），判断是否能由此充分地得出结论“欧洲国家的冰雪运动实力强于其它国家”，说明你的理由.

(2)、记图中斩获金牌次数大于70的国家为“冰雪运动强国”，请按照图中数据补全2×2列联表，并判断是否有97.5%的把握认为一个国家是否为“冰雪运动强国”与该国家所在地区（欧洲/其它）有关（假设该样本可以反映总体情况）.
附： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ .
$P (K^{2} \geq k_{0})$
0.10
0.05
0.025
0.010
$k_{0}$
2.706
3.841
5.024
6.635

“冰雪运动强国”
非“冰雪运动强国”
合计
欧洲国家
其它国家
合计

查看试题解析
20. 如图，在三棱锥 $P - A B C$ 中，平面 $P A C ⊥$ 平面 $A B C$ ， $△ P A C$ 为等边三角形， $A B ⊥ A C$ ， $D$ 是 $B C$ 的中点．

(1)、证明： $A C ⊥ P D$ ；

(2)、若 $A B = A C = 2$ ，求二面角 $C - P B - A$ 的余弦值．

查看试题解析
21. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{2}}{2}$ ，点 $M (- 2 ， 1)$ 为椭圆C上一点.

(1)、求椭圆C的方程；

(2)、过 $N (1 ， 0)$ 且斜率存在的直线AB交椭圆C于A、B两点，记 $t = \vec{M A} \cdot \vec{M B}$ ，若t的最大值和最小值分别为 $t_{1}$ 、 $t_{2}$ ，求 $t_{1} + t_{2}$ 的值.

查看试题解析
22. 设函数 $f (x) = x^{2} + m l n (x + 1) (m \in R)$ ．

(1)、若 $m = - 1$ ，当 $x \in (1 ， + \infty)$ 时，求证： $f (x) < x^{3}$ ；

(2)、若函数 $f (x)$ 在区间 $(0 ， 1)$ 上存在唯一零点，求实数 $m$ 的取值范围.

查看试题解析

$P (K^{2} \geq k_{0})$	0.10		0.05	0.025	0.010
$k_{0}$	2.706		3.841	5.024	6.635
		“冰雪运动强国”		非“冰雪运动强国”	合计
欧洲国家
其它国家
合计