广东省惠州市博罗县2021-2022学年高二下学期数学期中考试试卷
试卷更新日期:2022-06-13 类型:期中考试
一、单选题
-
1. 设函数在上存在导函数 , 的图象在点处的切线方程为 , 那么( )A、2 B、1 C、 D、2. 2022年北京冬奥会期间,准备从5名志愿者中选3人去为速度滑冰、花样滑冰、冰球三个竞赛项目服务,每个项目必须有志愿者参加且每名志愿者只服务一个项目,不同的安排方法种数为( ).A、12 B、24 C、36 D、603. 展开式中的常数项为( ).A、540 B、18 C、15 D、1354. 已知函数的导函数为 , 且满足 , 则( )A、 B、-1 C、 D、5. 学校要求学生从物理、历史、化学、生物、政治、地理这6科中选3科参加考试,规定先从物理和历史中任选1科,然后从其他4科中任选2科,不同的选法种数为( )A、5 B、12 C、20 D、1206. 的展开式中的系数是12,则实数a的值为( )A、4 B、5 C、6 D、77. 函数的图象大致为( )A、
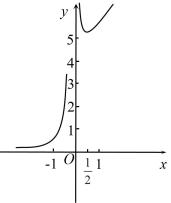 B、
B、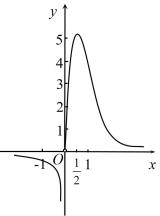 C、
C、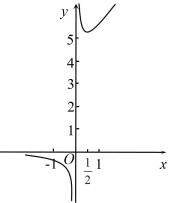 D、
D、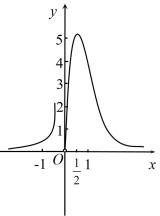 8. 已知是定义在R上的偶函数,是的导函数,当时, , 且 , 则的解集是( )A、 B、 C、 D、
8. 已知是定义在R上的偶函数,是的导函数,当时, , 且 , 则的解集是( )A、 B、 C、 D、二、多选题
-
9. 下列求导错误的是( ).A、 B、 C、 D、10. 离散型随机变量X的分布列为:
X
0
1
2
4
5
P
q
0.3
0.2
0.2
0.1
若离散型随机变量Y满足 , 则下列结果正确的有( )
A、 B、 C、 D、11. 已知函数 , 则( ).A、的递增区间为 B、极大值为 C、的极大值点为e D、12. 从有大小和质地相同的3个红球和2个蓝球的袋子中,每次随机摸出1个球,摸出的球不再放回,则( ).A、第一次摸到红球的概率为 B、第二次摸到红球的概率为 C、在第一次摸到蓝球的条件下,第二次摸到红球的概率为 D、在前两次都摸到蓝球的条件下,第三次摸到红球的概率为三、填空题
-
13. 在分布中,设 , 则.14. 杨辉三角在我国南宋数学家杨辉1261年所著的《详解九章算法》一书中被记载.它的开头几行如图所示,它包含了很多有趣的组合数性质,如果将杨辉三角从第1行开始的每一个数都换成分数 , 得到的三角形称为“莱布尼茨三角形”,莱布尼茨由它得到了很多定理,甚至影响到了微积分的创立,请问“莱布尼茨三角形”第9行第4个数是 .
杨辉三角
莱布尼茨三角形
第0行第1行
第2行
第3行
第n行
11 1
1 2 1
1 3 3 1
1 … 1
1
第0行
第1行
第2行
第3行
15. 若函数在上单调递增,则的取值范围为 .16. 已知函数 , 则函数的最小值为 . 若函数有3个零点,则k的范围是 .四、解答题
-
17. 从6名运动员中选4人参加4×100米接力赛,在下列条件下,各有多少种不同的排法?(1)、甲不在第一棒;(2)、若甲、乙两人都被选且必须跑相邻两棒.18. 设函数 .(1)、求在处的切线方程;(2)、求函数的极值.19. 设曲线在点处取得极值.(1)、求的单调区间;(2)、若 , 且恒成立,求m的取值范围.20. 为了纪念伟大的爱国主义诗人屈原,端午节包粽子已是我们的传统习俗.现有甲、乙两个箱子装有大小、外观均相同的粽子,已知甲箱中有5个蛋黄馅的粽子和3个红豆馅的粽子,乙箱中有4个蛋黄馅的粽子和3个红豆馅的粽子.(1)、若从甲箱中任取2个粽子,求这2个粽子都是红豆馅的概率;(2)、若先从甲箱中任取2个粽子放入乙箱中,然后再从乙箱中任取1个粽子,求取出的这个粽子是蛋黄馅的概率.21. 为响应绿色出行,某市推出新能源租赁汽车.每次租车的收费由两部分组成:①里程计费:1元/公里;②时间计费:0.12元/分.已知陈先生的家距离公司12公里,每天上下班租用该款汽车各一次.一次路上开车所用的时间记为t(分),现统计了50次路上开车所用时间,在各时间段内频数分布情况如下表所示.
时间t(分)
次数
12
28
8
2
将各时间段发生的频率视为概率,一次路上开车所用的时间视为用车时间,范围为.
(1)、估计陈先生一次租用新能源汽车所用的时间不低于30分钟的概率;(2)、求陈先生一次路上开车所用的时间t(分)的分布列和数学期望(同一区间内的值都看作该区间的中点值);(3)、若公司每月发放800元的交通补助,请估计是否足够陈先生一个月上下班租用新能源汽车(每月按22天计算),并说明理由.22. 已知函数 .(1)、若 , 讨论的单调性;(2)、若 , , 证明:只有1个零点.