【高考真题】2022年新高考数学真题试卷(浙江卷)
试卷更新日期:2022-06-13 类型:高考真卷
一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 设集合 ,则 ( )A、{2} B、 C、 D、2. 已知 ( 为虚数单位),则( )A、 B、 C、 D、3. 若实数x,y满足约束条件 则 的最大值是( )A、20 B、18 C、13 D、64. 设 ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件5. 某几何体的三视图如图所示(单位: ),则该几何体的体积(单位: )是( )
 A、 B、 C、 D、6. 为了得到函数 的图象,只要把函数 图象上所有的点( )A、向左平移 个单位长度 B、向右平移 个单位长度 C、向左平移 个单位长度 D、向右平移 个单位长度7. 已知 ,则 ( )A、25 B、5 C、 D、8. 如图,已知正三棱柱 ,E,F分别是棱 上的点.记 与 所成的角为 , 与平面 所成的角为 ,二面角 的平面角为 ,则( )
A、 B、 C、 D、6. 为了得到函数 的图象,只要把函数 图象上所有的点( )A、向左平移 个单位长度 B、向右平移 个单位长度 C、向左平移 个单位长度 D、向右平移 个单位长度7. 已知 ,则 ( )A、25 B、5 C、 D、8. 如图,已知正三棱柱 ,E,F分别是棱 上的点.记 与 所成的角为 , 与平面 所成的角为 ,二面角 的平面角为 ,则( ) A、 B、 C、 D、9. 已知 ,若对任意 ,则( )A、 B、 C、 D、10. 已知数列 满足 ,则( )A、 B、 C、 D、
A、 B、 C、 D、9. 已知 ,若对任意 ,则( )A、 B、 C、 D、10. 已知数列 满足 ,则( )A、 B、 C、 D、二、填空题:本大题共7小题,单空题每题4分,多空题每空3分,共36分.
-
11. 我国南宋著名数学家秦九韶,发现了从三角形三边求面积的公式,他把这种方法称为“三斜求积”,它填补了我国传统数学的一个空白.如果把这个方法写成公式,就是 ,其中a,b,c是三角形的三边,S是三角形的面积.设某三角形的三边 ,则该三角形的面积 .12. 已知多项式 ,则 , .13. 若 ,则 , .14. 已知函数 则 ;若当 时, ,则 的最大值是 .15. 现有7张卡片,分别写上数字1,2,2,3,4,5,6.从这7张卡片中随机抽取3张,记所抽取卡片上数字的最小值为 ,则 , .16. 已知双曲线 的左焦点为F,过F且斜率为 的直线交双曲线于点 ,交双曲线的渐近线于点 且 .若 ,则双曲线的离心率是 .17. 设点P在单位圆的内接正八边形 的边 上,则 的取值范围是 .
三、解答题:本大题共5小题,共74分.
-
18. 在 中,角A,B,C所对的边分别为a,b,c.
已知 .
(Ⅰ)求 的值;
(Ⅱ)若 ,求 的面积.
19. 如图,已知 和 都是直角梯形, , , , , , ,二面角 的平面角为 .设M,N分别为 的中点.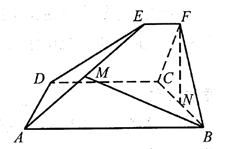
(Ⅰ)证明: ;
(Ⅱ)求直线 与平面 所成角的正弦值.