初中数学浙教版八下数学综合题优生特训7
试卷更新日期:2022-06-11 类型:复习试卷
一、综合题
-
1. 如图,在平面直角坐标系中,点O是坐标原点,四边形 是菱形,点A的坐标为 ,点C在x轴的正半轴上,直线 交y轴于点M, 边交y轴于点H,连接 .
 (1)、菱形 的边长是;(2)、求直线 的解析式;(3)、动点P从点A出发,沿折线 方向以2个单位/秒的速度向终点C匀速运动,设 的面积为 ,点P的运动时间为t秒,当点P在 边上运动时,求S与t间的函数关系式.2. 如图,在平面直角坐标系中,直线 : 分别与x轴、y轴交于点B、C,且与直线 : 交于点A.
(1)、菱形 的边长是;(2)、求直线 的解析式;(3)、动点P从点A出发,沿折线 方向以2个单位/秒的速度向终点C匀速运动,设 的面积为 ,点P的运动时间为t秒,当点P在 边上运动时,求S与t间的函数关系式.2. 如图,在平面直角坐标系中,直线 : 分别与x轴、y轴交于点B、C,且与直线 : 交于点A. (1)、分别求出点A、B、C的坐标;(2)、若D是线段 上的点,且 的面积为12,求直线 的函数表达式;(3)、在(2)的条件下,设P是射线 上的点,在平面内里否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.3. 如图,在平行四边形 中, 的平分线交 于点E,交 的延长线于F,以 为邻边作平行四边形 。
(1)、分别求出点A、B、C的坐标;(2)、若D是线段 上的点,且 的面积为12,求直线 的函数表达式;(3)、在(2)的条件下,设P是射线 上的点,在平面内里否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.3. 如图,在平行四边形 中, 的平分线交 于点E,交 的延长线于F,以 为邻边作平行四边形 。 (1)、证明平行四边形 是菱形;(2)、若 ,连结 ,①求证: ;②求 的度数;(3)、若 , , ,M是 的中点,求 的长。4. 如图1,正方形ABCD的顶点A、D分别在平行线l1、l2上,由B、D向l1作垂线,垂足分别为M、N.
(1)、证明平行四边形 是菱形;(2)、若 ,连结 ,①求证: ;②求 的度数;(3)、若 , , ,M是 的中点,求 的长。4. 如图1,正方形ABCD的顶点A、D分别在平行线l1、l2上,由B、D向l1作垂线,垂足分别为M、N.

 (1)、求证:AM=DN;(2)、如图2,正方形AEFG的顶点E在直线l2上,过点F、C分别作l2的垂线段FP、CQ,求证:FP+CQ=DE;(3)、如图3,正方形AEFG的顶点A、G在直线l1上,顶点E、F在直线l2上,连接BG并延长交l2于点R,若∠BRD=30°,AE= ,求AB.5. 如图,已知在矩形ABCD中,点E在AB边上,F在CE边上,且∠ACD=∠DAF.
(1)、求证:AM=DN;(2)、如图2,正方形AEFG的顶点E在直线l2上,过点F、C分别作l2的垂线段FP、CQ,求证:FP+CQ=DE;(3)、如图3,正方形AEFG的顶点A、G在直线l1上,顶点E、F在直线l2上,连接BG并延长交l2于点R,若∠BRD=30°,AE= ,求AB.5. 如图,已知在矩形ABCD中,点E在AB边上,F在CE边上,且∠ACD=∠DAF. (1)、当∠CAF=30°时,求矩形的长宽之比;(2)、若∠CAF=∠ECB,请回答下列问题;
(1)、当∠CAF=30°时,求矩形的长宽之比;(2)、若∠CAF=∠ECB,请回答下列问题;①设∠ACE=x,∠CAF=y,求y关于x的表达式;
②若EB=1,求CF的长.
6. 如图,在平面直角坐标系中,已知点A(-6,0),B(0,8),点C为OB的中点,点D在第二象限,四边形AOCD为矩形,直线AB交DC于点E. (1)、求直线AB的解析式及点E的坐标;(2)、动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时,动点N从点A出发沿线段AO以每秒2个单位长度的速度向终点O运动,当其中一点到达终点时,两点同时停止运动. 连接NP, 设点P的运动时间为 秒.
(1)、求直线AB的解析式及点E的坐标;(2)、动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时,动点N从点A出发沿线段AO以每秒2个单位长度的速度向终点O运动,当其中一点到达终点时,两点同时停止运动. 连接NP, 设点P的运动时间为 秒.①当 为何值时,四边形ANPE 为平行四边形?
②当 为何值时,四边形ANPD 为矩形?
7. 如图1,在平面直角坐标系中,直线y= x+n分别与x轴、y轴交于点A、B,且点A的坐标为(4,0),点C为线段AB的中点. (1)、求点B的坐标;(2)、点P为直线AB上的一个动点,过点P作x轴的垂线,与直线OC交于点Q,设点P的横坐标为m,△OPQ的面积为S,求S与m的函数解析式;(3)、当点P在直线AB上运动时,在平面直角坐标系内是否存在一点N,使得以O,B,P,N为顶点的四边形为矩形,若存在,求出N点的坐标;若不存在,请说明理由.8. 如图,平行四边形ABCD中AB∥CD,AD∥BC,点G是线段BC的中点,点E是线段AD上的一点,点F是线段AB延长线上一点,连接DF,且∠ABE=∠CDG=∠FDG.
(1)、求点B的坐标;(2)、点P为直线AB上的一个动点,过点P作x轴的垂线,与直线OC交于点Q,设点P的横坐标为m,△OPQ的面积为S,求S与m的函数解析式;(3)、当点P在直线AB上运动时,在平面直角坐标系内是否存在一点N,使得以O,B,P,N为顶点的四边形为矩形,若存在,求出N点的坐标;若不存在,请说明理由.8. 如图,平行四边形ABCD中AB∥CD,AD∥BC,点G是线段BC的中点,点E是线段AD上的一点,点F是线段AB延长线上一点,连接DF,且∠ABE=∠CDG=∠FDG. (1)、∠A=45°,∠ADF=75°, ,求线段BC的长;(2)、求证:AB=BF+DF .9. 已知如图1,四边形 是正方形, .
(1)、∠A=45°,∠ADF=75°, ,求线段BC的长;(2)、求证:AB=BF+DF .9. 已知如图1,四边形 是正方形, .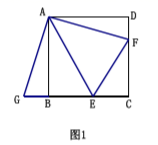 (1)、如图1,若点 分别在边 上,延长线段 至 ,使得 ,若 求 的长;(2)、如图2,若点 分别在边 延长线上时,求证:
(1)、如图1,若点 分别在边 上,延长线段 至 ,使得 ,若 求 的长;(2)、如图2,若点 分别在边 延长线上时,求证: (3)、如图3,如果四边形 不是正方形,但满足 且 ,请你直接写出 的长.
(3)、如图3,如果四边形 不是正方形,但满足 且 ,请你直接写出 的长. 10. 如图,在菱形ABCD中,∠A=60°,E为菱形ABCD内对角线BD左侧一点,连接BE、CE、DE.
10. 如图,在菱形ABCD中,∠A=60°,E为菱形ABCD内对角线BD左侧一点,连接BE、CE、DE.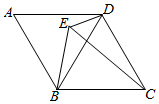 (1)、若AB=6,求菱形ABCD的面积;(2)、若∠BED=2∠A,求证:CE=BE+DE.11. 如图l,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连结EB,过点A作AM BE,垂足为M,AM交BD于点F.
(1)、若AB=6,求菱形ABCD的面积;(2)、若∠BED=2∠A,求证:CE=BE+DE.11. 如图l,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连结EB,过点A作AM BE,垂足为M,AM交BD于点F.
 (1)、求证:OE=OF;(2)、如图2,若点E在AC的延长线上,AM BE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗.如果成立,请给出证明;如果不成立,请说明理由.12. 矩形ABCD中,AB=3,BC=4.点E,F在对角线AC上,点M,N分别在边AD,BC上.
(1)、求证:OE=OF;(2)、如图2,若点E在AC的延长线上,AM BE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗.如果成立,请给出证明;如果不成立,请说明理由.12. 矩形ABCD中,AB=3,BC=4.点E,F在对角线AC上,点M,N分别在边AD,BC上. (1)、如图1,若AE=CF=1,M,N分别是AD,BC的中点.求证:四边形EMFN为矩形.(2)、如图2,若AE=CF=0.5, ,且四边形EMFN为矩形,求x的值.13. 如图,已知正方形ABCD的边长为2,两条对角线相交于点O,以O为顶点作正方形OEFG,将正方形OEFG绕点O旋转.
(1)、如图1,若AE=CF=1,M,N分别是AD,BC的中点.求证:四边形EMFN为矩形.(2)、如图2,若AE=CF=0.5, ,且四边形EMFN为矩形,求x的值.13. 如图,已知正方形ABCD的边长为2,两条对角线相交于点O,以O为顶点作正方形OEFG,将正方形OEFG绕点O旋转. (1)、旋转过程中,正方形OEFG与正方形ABCD重叠部分的面积为(2)、连接BG,EC,延长EC交BG于点H,判断EC与BG的位置关系,并说明理由;(3)、连接DE,当以B、D、E、C为顶点的四边形是平行四边形时,求点D到OE的距离14. 在菱形 中,点E为边 的中点, ,垂足为点 , 垂足为点G.
(1)、旋转过程中,正方形OEFG与正方形ABCD重叠部分的面积为(2)、连接BG,EC,延长EC交BG于点H,判断EC与BG的位置关系,并说明理由;(3)、连接DE,当以B、D、E、C为顶点的四边形是平行四边形时,求点D到OE的距离14. 在菱形 中,点E为边 的中点, ,垂足为点 , 垂足为点G. (1)、如图①,求证: ;(2)、如图②,如图③,请分别写出线段 之间的数量关系,不需要证明;(3)、在(1)(2)的条件下,若菱形 的面积为 ,菱形 的周长为 ,四边形 的面积为 , 线段 的长为 .15. 如图,在菱形ABCD中, , ,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
(1)、如图①,求证: ;(2)、如图②,如图③,请分别写出线段 之间的数量关系,不需要证明;(3)、在(1)(2)的条件下,若菱形 的面积为 ,菱形 的周长为 ,四边形 的面积为 , 线段 的长为 .15. 如图,在菱形ABCD中, , ,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.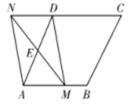 (1)、求证:四边形AMDN是平行四边形;(2)、当AM的值为时,四边形AMDN是矩形;(3)、若 ,求证:四边形AMDN是菱形.16. 如图
(1)、求证:四边形AMDN是平行四边形;(2)、当AM的值为时,四边形AMDN是矩形;(3)、若 ,求证:四边形AMDN是菱形.16. 如图 (1)、如图1所示,已知正方形 中, 是 上一点, 是 延长线上一点,且 .求证: ;(2)、如图2所示,在正方形 中, 是 上一点, 是 上一点,如果 ,请利用(1)中的结论证明: .17. 如图,在平行四边形 中,点P是 边上一点(不与A,B重合), ,过点P作 ,交 边于点Q,连结 .
(1)、如图1所示,已知正方形 中, 是 上一点, 是 延长线上一点,且 .求证: ;(2)、如图2所示,在正方形 中, 是 上一点, 是 上一点,如果 ,请利用(1)中的结论证明: .17. 如图,在平行四边形 中,点P是 边上一点(不与A,B重合), ,过点P作 ,交 边于点Q,连结 .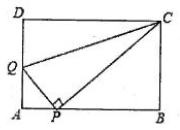 (1)、若 ,求证:四边形 是矩形;(2)、在(1)的条件下,当 , 时,求 的长.18. 如图正方形ABCD,点E、G、H分别在AB、AD、BC上,DE与HG相交于点O.
(1)、若 ,求证:四边形 是矩形;(2)、在(1)的条件下,当 , 时,求 的长.18. 如图正方形ABCD,点E、G、H分别在AB、AD、BC上,DE与HG相交于点O. (1)、如图1,当∠GOD=90°,
(1)、如图1,当∠GOD=90°,①求证:DE=HG
②平移图1中线段GH,使G点与D重合,H点在BC延长线上,连接EH,取EH中点P,连接PC,如图2,求证:BE= PC;
(2)、如图3,当∠GOD=45°,边长AB=4,HG= ,则DE的长为(直接写出结果).19. 如图,在矩形ABCD中,AD=nAB,E,F分别在AB,BC上. (1)、若n=1,AF⊥DE.
(1)、若n=1,AF⊥DE.①如图1,求证:AE=BF;
②如图2,点G为CB延长线上一点,DE的延长线交AG于H,若AH=AD,求证:AE+BG=AG;
(2)、如图3,若E为AB的中点,∠ADE=∠EDF.则 的值是(结果用含n的式子表示).20. 在平面直角坐标系中,点O为坐标原点,点 ,点 ,点 在第一象限内.(1)、若点C在直线 上,求点 的值;(2)、若直线AB的解析式为: ,求证:四边形OABC为菱形;(3)、直线AC与直线OB相交于点 ,则在射线OB上是否存在点G使得 是直角三角形.若存在请求出点G坐标,若不存在,请说明理由.21. 如图, 平行四边形 中, , , , 是 的中点, 是边 上的动点, 的延长线与 的延长线交于点 ,连接CE, . (1)、求证:四边形 是平行四边形;(2)、①当 的长为多少时,四边形 是矩形;
(1)、求证:四边形 是平行四边形;(2)、①当 的长为多少时,四边形 是矩形;②当 时,四边形 是菱形,(直接写出答案,不需要说明理由).
22. 如图,在菱形ABCD中,AB=2cm,∠ADC=120°.动点E、F分别从点B、D同时出发,都以0.5cm/s的速度向点A、C运动,连接AF、CE,分别取AF、CE的中点G、H.设运动的时间为ts (0<t<4). (1)、求证:AF∥CE;(2)、当t为何值时,△ADF的面积为 cm2;(3)、连接GE、FH.当t为何值时,四边形EHFG为菱形.23. 平面直角坐标系中,点A、点B的坐标分别是(﹣4,0)、(0,2).
(1)、求证:AF∥CE;(2)、当t为何值时,△ADF的面积为 cm2;(3)、连接GE、FH.当t为何值时,四边形EHFG为菱形.23. 平面直角坐标系中,点A、点B的坐标分别是(﹣4,0)、(0,2). (1)、求直线AB的解析式;(2)、如图1,点P是直线AB上一点,若△AOP的面积是△AOB面积的2倍,求点P的坐标;(3)、若点P满足(2)的条件,且在第一象限内,如图2.点M是y轴负半轴上一动点,连接PM,过点P作PN⊥PM,交x轴于点N.当点M运动时,(ON﹣OM)的值是否为定值?若是,请求出它的值;若不是,请说明理由.24. 如图,菱形ABCD的边长为12cm,∠A=60°,动点P从点A出发,沿着线路AB—BD做匀速运动,动点Q从点D同时出发,沿着线路DC-CB-BA做匀速运动.
(1)、求直线AB的解析式;(2)、如图1,点P是直线AB上一点,若△AOP的面积是△AOB面积的2倍,求点P的坐标;(3)、若点P满足(2)的条件,且在第一象限内,如图2.点M是y轴负半轴上一动点,连接PM,过点P作PN⊥PM,交x轴于点N.当点M运动时,(ON﹣OM)的值是否为定值?若是,请求出它的值;若不是,请说明理由.24. 如图,菱形ABCD的边长为12cm,∠A=60°,动点P从点A出发,沿着线路AB—BD做匀速运动,动点Q从点D同时出发,沿着线路DC-CB-BA做匀速运动. (1)、求BD的长.(2)、已知动点P运动的速度为2cm/s,动点Q运动的速度为2.5cm/s.经过12秒后,P、Q分别到达M、N两点,试判断△AMN的形状,并说明理由.(3)、设问题(2)中的动点P、Q分别从M、N同时沿原路返回,动点P的速度不变,动点Q的速度改变为acm/s,经过3秒后,P、Q分别到达E、F两点,若△BEF为直角三角形,试求a值.25. 如图,在直角坐标系中, , , ,点D在 上, , 于H.
(1)、求BD的长.(2)、已知动点P运动的速度为2cm/s,动点Q运动的速度为2.5cm/s.经过12秒后,P、Q分别到达M、N两点,试判断△AMN的形状,并说明理由.(3)、设问题(2)中的动点P、Q分别从M、N同时沿原路返回,动点P的速度不变,动点Q的速度改变为acm/s,经过3秒后,P、Q分别到达E、F两点,若△BEF为直角三角形,试求a值.25. 如图,在直角坐标系中, , , ,点D在 上, , 于H. (1)、判断 的形状,并说明理由.(2)、求点D的坐标.(3)、若P是 上的动点,当 的周长最小时,求 的面积.26. 如图,在平面直角坐标系中,O为原点,已知直线y=﹣ x+4与x轴交于点A,与y轴交于点B.
(1)、判断 的形状,并说明理由.(2)、求点D的坐标.(3)、若P是 上的动点,当 的周长最小时,求 的面积.26. 如图,在平面直角坐标系中,O为原点,已知直线y=﹣ x+4与x轴交于点A,与y轴交于点B. (1)、点A的坐标为 , 点B的坐标为;(2)、如图①,若点M(x,y)在线段AB上运动(不与端点A、B重合),连接OM,设 的面积为S,写出S关于x的函数解析式,并写出自变量x的取值范围;(3)、如图②,点C在直线AB上,若四边形OADC是菱形,求菱形对角线OD的长.27. 如图,直线y=﹣2x+8分别交x轴,y轴于点A , B , 直线y x+3交y轴于点C , 两直线相交于点D .
(1)、点A的坐标为 , 点B的坐标为;(2)、如图①,若点M(x,y)在线段AB上运动(不与端点A、B重合),连接OM,设 的面积为S,写出S关于x的函数解析式,并写出自变量x的取值范围;(3)、如图②,点C在直线AB上,若四边形OADC是菱形,求菱形对角线OD的长.27. 如图,直线y=﹣2x+8分别交x轴,y轴于点A , B , 直线y x+3交y轴于点C , 两直线相交于点D .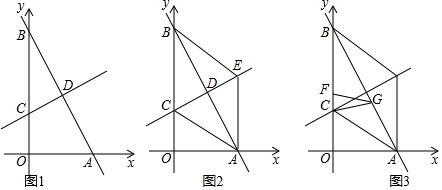 (1)、求点D的坐标;(2)、如图2,过点A作AE∥y轴交直线y x+3于点E , 连接AC , BE . 求证:四边形ACBE是菱形;(3)、如图3,在(2)的条件下,点F在线段BC上,点G在线段AB上,连接CG , FG , 当CG=FG , 且∠CGF=∠ABC时,求点G的坐标.28. 正方形ABCD与正方形CEFG的位置如图所示,点G在线段CD或CD的延长线上,分别连接BD、BF、FD,得到
(1)、求点D的坐标;(2)、如图2,过点A作AE∥y轴交直线y x+3于点E , 连接AC , BE . 求证:四边形ACBE是菱形;(3)、如图3,在(2)的条件下,点F在线段BC上,点G在线段AB上,连接CG , FG , 当CG=FG , 且∠CGF=∠ABC时,求点G的坐标.28. 正方形ABCD与正方形CEFG的位置如图所示,点G在线段CD或CD的延长线上,分别连接BD、BF、FD,得到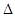 BFD.
(1)、在图1、图2、图3中,若正方形CEFG的边长分别为1、3、4,且正方形ABCD的边长均为3,请通过计算填写下表:
BFD.
(1)、在图1、图2、图3中,若正方形CEFG的边长分别为1、3、4,且正方形ABCD的边长均为3,请通过计算填写下表:
正方形CEFG的边长
1
3
4
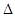 BFD的面积(2)、若正方形CEFG的边长为a,正方形ABCD的边长为 ,猜想 的大小,并结合图3证明你的猜想.
BFD的面积(2)、若正方形CEFG的边长为a,正方形ABCD的边长为 ,猜想 的大小,并结合图3证明你的猜想.

