初中数学浙教版八下数学综合题优生特训6

试卷更新日期：2022-06-11 类型：复习试卷

进入出卷网下载

一、综合题

1. 如图，在长方形ABCD种，AB＝3，BC＝6，动点P从点A出发，沿射线AD方向以每秒3个单位长度的速度运动；同时Q从点B出发，沿射线BC方向以每秒1个单位长度的速度运动.设点P，Q的运动时间为t（秒）.

(1)、当t＝2时，求线段PQ的长；

(2)、当线段PQ与线段DC相交于点M，且DM＝CM时，求t的值；

(3)、连接AQ，是否存在某一时刻，△APQ为等腰三角形？若存在，求出此时△APQ的面积；若不存在，请说明理由.

查看试题解析
2. 如图，菱形 $A B C D$ 的对角线 $A C$ 和 $B D$ 交于点O，分别过点 $B ， C$ 作 $C E / / B D ， B E / / A C$ ， $C E$ 和 $B E$ 交于点E．

(1)、求证：四边形 $O B E C$ 是矩形；

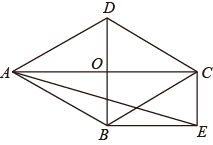(2)、当 $∠ B A D = 60 ° ， A D = 2 \sqrt{3}$ 时，求 $E A$ 的长．

查看试题解析
3. 如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作AE⊥BC于点E，延长BC到点F，使得CF=BE，连接DF，

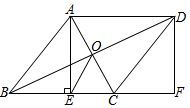(1)、求证：四边形AEFD是矩形；

(2)、连接OE，若AB＝13，OE＝2 $\sqrt{13}$ ，求AE的长．

查看试题解析
4. 如图，在矩形ABCD中，点E，F分别是边AB，CD的中点，连接EF．

(1)、求证 $E F ⊥ A B$ ；

(2)、点H是BC上一点，连接AH，将 $△ A B H$ 沿AH翻折，得到 $△ A G H$ ，点B的对应点G落在EF上，若 $A B = 2$ ，求AH的长．

查看试题解析
5. 如图，平行四边形ABCD中，AB=4cm，BC=6cm，∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连接CE，DF．

(1)、求证：四边形CEDF是平行四边形；

(2)、请直接写出当AE为何值时，四边形CEDF是菱形（不用证明）．

(3)、当AE＝4时，请证明：四边形CEDF是矩形．

查看试题解析
6. 如图，长方形ABCD中，长 $A D = 10$ cm，宽 $A B = 6$ cm，动点P在折线 $A D - D C$ 上从A向C移动（点P不与点C重合），设点P运动的路径长为xcm， $△ B C P$ 的面积为 $y$ cm² ．

(1)、当点P在AD上运动时， $△$ BCP的面积，当点P在DC上运动时， $△$ BCP的面积（填“增大”“减小”或“不变”）

(2)、求y关于x的函数表达式，并指出自变量x的取值范围；

(3)、当x为何值时， $△$ BCP为等腰三角形．

查看试题解析
7. 如图，在平面直角坐标系xOy中，直线l：y=2x-4与x轴交于点A，与y轴交于点B.

(1)、求点A，B的坐标.

(2)、若P是直线x=-2上的一动点，则在坐标平面内是否存在点Q，使得以A，B，P，Q为顶点的四边形是菱形？若存在，求出点Q的坐标；若不存在，请说明理由.

查看试题解析
8. 如图，平行四边形ABCD中，点O是对角线AC的中点，点M为BC上一点，连接AM，且AB＝AM.AE为△ABM边BM的中线，AF⊥AB，EG⊥GD，延长FO交AB于点N.

(1)、若BM＝4，MC＝6，AC＝10，求AM的长度：

(2)、若∠ACB＝45°，求证：AN+AF＝2FG.

查看试题解析
9. 如图，在矩形ABCD中，AB＝6，AD＝8，P，E分别是线段AC、BC上的点，且四边形PEFD为矩形.

(1)、若△PCD是等腰三角形时，求AP的长；

(2)、求证：PC⊥CF.

查看试题解析
10. 如图1所示，菱形ABCD的顶点A，B在x轴上，点A在点B的左侧，点D在y轴的正半轴上，其中点B（ $\frac{9}{2}$ ，0）、D（0，6）.

(1)、求C点的坐标；

(2)、如图2，E是AD上一点，且AE＝ $\frac{11}{4}$ ，P是AC上一动点，求PD+PE的最小值；

(3)、如图3，动点Q从点B出发，以每秒 $\frac{5}{4}$ 个单位长度的速度，沿折线B→C→D在菱形的两边上匀速运动，设运动时间为t秒.若点Q到BD的距离是 $\frac{5}{2}$ ，则t＝.

查看试题解析
11. 在平面直角坐标系中，直线 $y = - 3 x - \frac{5}{2}$ 交x轴于点A，交y轴于点B，直线 $y = - \frac{3}{4} x + 3$ 交x轴于点C，交y轴于点D.

(1)、如图1，连接 $B C$ ，求 $△ B C D$ 的面积；

(2)、如图2，在直线 $y = - \frac{3}{4} x + 3$ 上存在点E，使得 $∠ A B E = 45 °$ ，求点E的坐标；

(3)、如图3，在 $(2)$ 的条件下，连接 $O E$ ，过点 $E$ 作 $C D$ 的垂线交y轴于点F，点P在直线 $E F$ 上，在平面中存在一点Q，使得以 $O E$ 为一边， $O ， E ， P ， Q$ 为顶点的四边形为菱形，请直接写出点Q的坐标.

查看试题解析
12. 已知四边形 $A B C D$ 是矩形.

(1)、如图1， $E 、 F$ 分别是 $A B 、 A D$ 上的点， $C E$ 垂直平分 $B F$ ，垂足为G，连接 $D G$ .
①求证： $D G = C G$ ；

②若 $B C = 2 A B$ ，求 $∠ D G C$ 的大小；

(2)、如图2， $A B = B C = 6$ ， $M 、 N 、 P$ 分别是 $A B 、 C D 、 A D$ 上的点， $M N$ 垂直平分 $B P$ ，点Q是 $C D$ 的中点，连接 $M P ， P Q$ ，若 $P Q ⊥ M P$ ，直接写出 $C N$ 的长.

查看试题解析
13. 已知：正方形ABCD

(1)、如图，E，F分别是正方形ABCD的边CB，DC延长线上的点，且BE=CF，过点E作EG//BF，交正方形外角的平分线CG于点G，连接GF.
求证：

① $A E ⊥ B F$ ；

②求证：四边形BRGF是平行四边形.

(2)、如图，点E，F将对角线AC三等分，且AC=12，点P在正方形的边上，分类说明满足PE+PF=9的点P的位置情况.

查看试题解析
14. 在平面直角坐标系中，直线 $y = k x - 4 k + 4$ 过定点C， $B (0 ， m)$ （其中 $0 < m < 8$ ），点A在x轴的正半轴上且满足 $∠ ACB = 90 °$ .

(1)、如图1，直接写出定点C的坐标，直接写出点A的坐标（用含m的式子表示）.

(2)、如图2，作矩形AOBD，连接CD.
①当 $0 < m < 4$ 时，求 $\frac{O A - A D}{C D}$ 的值.

②是否存在m的值使得 $O A = 2 C D$ ？若存在，求出m的值；若不存在，举反例并说明理由.

查看试题解析
15. 如图，在矩形 $A B C D$ 中， $A D = 2 A B = 8$ ，点 $E$ 是边 $A D$ 的中点.连结 $E C$ ， $P$ ， $Q$ 分别是射线 $A D$ ， $E C$ 上的动点，且 $E Q = \sqrt{2} A P$ .连结 $B P$ ， $P Q$ .过点 $B$ ， $Q$ 分别作 $P Q$ ， $B P$ 的平行线交于点 $F$ .

(1)、当点 $P$ 在线段 $A E$ 上（不包含端点）时；
①求证：四边形 $B F Q P$ 是正方形；

②若 $B C$ 将四边形 $B F Q P$ 的面积分为 $1 ： 3$ 两部分，求 $A P$ 的长；

(2)、如图2，连结 $P F$ ，若点 $C$ 在对角线 $P F$ 上，求 $△ B F C$ 的面积（直接写出答案）.

查看试题解析
16. 如图，在平面直角坐标系中，点A的坐标为（﹣6，0），点B在y轴正半轴上，∠ABO＝30°，动点D从点A出发沿着射线AB方向以每秒3个单位的速度运动，过点D作DE⊥y轴，交y轴于点E，同时，动点F从定点C （1，0）出发沿x轴正方向以每秒1个单位的速度运动，连结DO，EF，设运动时间为t秒.

(1)、当点D运动到线段AB的中点时.
①求t的值；

②判断四边形DOFE是否是平行四边形，请说明理由.

(2)、点D在运动过程中，若以点D，O，F，E为顶点的四边形是矩形，求出满足条件的t的值.

查看试题解析
17. 已知，在平面直角坐标系中，一次函数y＝kx－3（k≠0）交x轴于点A，交y轴与点B.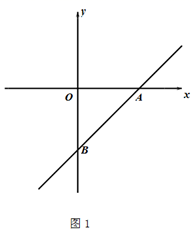

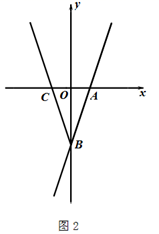
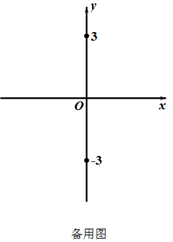(1)、如图1，若k＝1，求线段AB的长；

(2)、如图2，点C与点A关于y轴对称，作射线BC；
①若k＝3，请写出以射线BA和射线BC所组成的图形为函数图象的函数解析式；

② y轴上有一点D(0，3)，连接AD、CD，请判断四边形ABCD的形状并证明；若 $S_{四边形 ABCD}$ ≥9，求k的取值范围

查看试题解析
18. 如图，等腰△ABC中，已知AC＝BC＝ $\sqrt{10}$ ，AB＝2，作∠ACB的外角平分线CF，点E从点B沿着射线BA以每秒1个单位的速度运动，过点E作BC的平行线交CF于点F.

(1)、求证：四边形BCFE是平行四边形；

(2)、当点E是边AB的中点时，连接AF，试判断四边形AECF的形状，并说明理由；

(3)、设运动时间为t秒，是否存在t的值，使得以△EFC的其中两边为邻边所构造的平行四边形恰好是菱形？不存在的，试说明理由；存在的，请直接写出t的值.

查看试题解析
19. 如图，已知在正方形 $A B C D$ 中， $A B = 2$ ，点E为线段 $A C$ 上一点（点E不与A、C重合），
$D E$ ，过点E作 $E F ⊥ D E$ ．交射线 $B C$ 于点F，以 $D E$ 、 $E F$ 为邻边作矩形 $D E F G$ ．

(1)、求证： $D E = E F$ ；

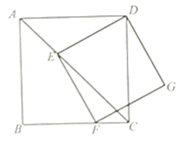
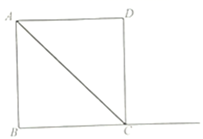(2)、连接 $C G$ 、 $E G$ ，设 $A E = x$ ， $△ E C G$ 的面积为y．求y关于x的函数关系式并写
出定义域；

(3)、设 $E G$ 、 $C D$ 相交于点H如果 $△ E D H$ 是等腰三角形，求线段 $A E$ 的长．

查看试题解析
20. 在图1，2，3中，已知 $▱ A B C D$ ， $∠ A B C = 120^{°}$ ，点E为线段 $B C$ 上的动点，连接 $A E$ ，以 $A E$ 为边向上作菱形 $A E F G$ ，且 $∠ E A G = 120^{°}$ ．

(1)、如图1，当点E与点B重合时， $∠ C E F =$ °；

(2)、如图2，连接 $A F$ ．
①填空： $∠ F A D$ ▲ $∠ E A B$ （填“>”，“<”，“=”）；

②求证：点F在 $∠ A B C$ 的平分线上；

(3)、如图3，连接 $E G$ ， $D G$ ，并延长 $D G$ 交 $B A$ 的延长线于点H，当四边形 $A E G H$ 是平行四边形时，求 $\frac{B C}{A B}$ 的值．

查看试题解析
21. 已知：如图已知直线 $A B$ 的函数解析式为 $y = - 2 x + 8$ ，与x轴交于点A，与y轴交于点B．

(1)、求A、B两点的坐标；

(2)、若点 $P (m ， n)$ 为线段 $A B$ 上的一个动点（与A、B不重合），作 $P E ⊥ x$ 轴于点E， $P F ⊥ y$ 轴于点F，连接 $E F$ ，问：
①若 $△ P A O$ 的面积为S，求S关于m的函数关系式，并写出m的取值范围；

②是否存在点P，使 $E F$ 的值最小？若存在，求出 $E F$ 的最小值；若不存在，请说明理由．

查看试题解析
22. 如图1，矩形ABCD中，点E，P，K分别在AB，AD，BC上，且DE⊥PK，DE＝PK.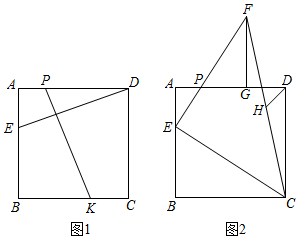

(1)、求证：四边形ABCD是正方形.

(2)、如图2，在（1）的条件下，△EFC是等腰直角三角形，∠CEF＝90°，FG⊥AD于点G.
①求证：AG＝FG；

②若点H为CF的中点，求 $\frac{D H}{D G}$ 的值.

查看试题解析
23. 问题情境：如图，在平面直角坐标系中，点O是坐标原点，四边形 $A B C O$ 是菱形，点A的坐标为 $(a ， b)$ ，且a和b满足 $a = \sqrt{b - 4} + \sqrt{4 - b} - 3$ ；点C在x轴的正半轴上，直线 $A C$ 交y轴于点M， $A B$ 边交y轴于点H，连接 $B M$ ；

(1)、求点A的坐标和菱形 $A B C O$ 的边长；

(2)、求直线 $A C$ 的解析式；

(3)、问题探究：
动点P从点A出发，沿折线 $A B C$ 方向以2个单位长度/秒的速度向终点C匀速运动，设 $Δ P M B$ 的面积为 $S (S \neq 0)$ ，点P的运动时间为t秒，

①求S与t之间的函数关系式；

②在点P运动过程中，当 $S = 3$ 时，请求出t的值.

查看试题解析
24. 如图，在正方形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点 $O$ ， $E$ 为 $B C$ 上一点， $C E = 4$ ， $F$ 为 $D E$ 的中点，若 $△ C E F$ 的周长为 $16$ ．

(1)、求 $C F$ 的长；

(2)、求 $O F$ 的长．

查看试题解析
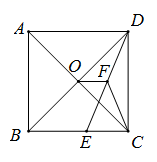25. 已知正方形ABCD，以CE为边在正方形ABCD外部作正方形CEFG，连AF，H是AF的中点，连接BH，HE．

(1)、如图1所示，点E在边CB上时，则BH，HE的关系为；

(2)、如图2所示，点E在BC延长线上，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请给出新的结论并证明．

(3)、如图3，点B，E，F在一条直线上，若 $A B = 13$ ， $C E = 5$ ，直接写出BH的长．

查看试题解析
26. 如图，在菱形ABCD，对角线AC，与BD交于点O，过点C作BD的平行线，过点D作AC的平行线，两直线交于点E，

(1)、求证：四边形OCED是矩形；

(2)、若CE=1，菱形ABCD的周长为 $4 \sqrt{5}$ ，求菱形ABCD的面积.

查看试题解析
27. 如图，已知四边形 $A B C D$ 和四边形 $C E F G$ 都是正方形，且 $A B > C E$ ，连接 $B G ， D E$ .

(1)、求证： $B G = D E$ ；

(2)、连接 $B D$ ，若 $C G$ // $B D$ ， $B G = B D$ ，求 $∠ B D E$ 的度数.

查看试题解析
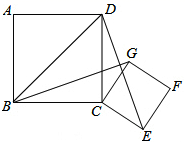28. △ABC中，点O是AC上一动点，过点O作直线MN $//$ BC，若MN交∠BCA的平分线于点E，交∠DCA的平分线于点F，连接AE、AF.

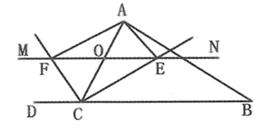(1)、说明： $O E = O F$ ；

(2)、当点O运动到AC中点处时，求证：四边形AECF是矩形；

(3)、在（2）的条件下，当△ABC满足什么条件时，四边形AECF为正方形，并加以证明.

查看试题解析
29. 如图，在菱形 $A B C D$ 中， $∠ A = 60^{°} ， A B = 4 ， E$ 是 $A D$ 边上的动点，作 $∠ B E F = 60^{°}$ 交 $C D$ 于点F，在 $A B$ 上取点G使 $A G = A E$ ，连结 $E G .$

(1)、求 $∠ E G B$ 的度数；

(2)、求证： $E F = B E ；$

(3)、若P是 $E F$ 的中点，当 $A E$ 为何值时， $Δ E G P$ 是等腰三角形.

查看试题解析
30. 如图正方形 $A B C D$ ， $D E$ 与 $H G$ 相交于点O（O不与D、E重合）.

(1)、如图（1），当 $∠ G O D = 90 °$ ，
①求证： $D E = G H$ ；

②求证： $G D + E H > \sqrt{2} D E$ ；

(2)、如图（2），当 $∠ G O D = 45 °$ ，边长 $A B = 4$ ， $H G = 2 \sqrt{5}$ ，求 $D E$ 的长.

查看试题解析