初中数学浙教版八下数学综合题优生特训4
试卷更新日期:2022-06-11 类型:复习试卷
一、综合题
-
1. 如图,将矩形 ABCD的四个角向内折起,恰好拼成一个无缝隙、无重叠的四边形 EFGH.
 (1)、判断四边形EFGH的形状,并说明理由;(2)、若EH=5,EF=12,则矩形ABCD的面积是.2. 如图,延长▱ABCD的边DC到点E,使CE=DC,连结AE,交BC于点F,连结AC,BE.
(1)、判断四边形EFGH的形状,并说明理由;(2)、若EH=5,EF=12,则矩形ABCD的面积是.2. 如图,延长▱ABCD的边DC到点E,使CE=DC,连结AE,交BC于点F,连结AC,BE. (1)、求证:BF=CF;(2)、若AB=2,AD=4,且∠AFC= 2∠D,求 ABCD的面积.3. 如图,在菱形ABCD中,CE⊥AB于点E.
(1)、求证:BF=CF;(2)、若AB=2,AD=4,且∠AFC= 2∠D,求 ABCD的面积.3. 如图,在菱形ABCD中,CE⊥AB于点E. (1)、若CE=4,AE=2BE,求菱形ABCD的周长.(2)、连结BD交CE于点F.
(1)、若CE=4,AE=2BE,求菱形ABCD的周长.(2)、连结BD交CE于点F.①若DF=BF+2EF,求证:AE=BE.
②设四边形AEFD和 的面积分别是 和 ,若 ,求线段BF的长.
4. 在△ABC中,∠ACB=90°,AC=BC,D为AB的中点,P是AB上的一个动点,PE⊥AC于点E,PF⊥BC于点F. (1)、求证:四边形EPFC是矩形.(2)、当点P运动到时,四边形EPFC是正方形.(3)、求证:DE=DF.5. 已知四边形ABCD为菱形,E为对角线AC上的一个动点,连结DE并延长交AB的延长线于点F,连结BE.
(1)、求证:四边形EPFC是矩形.(2)、当点P运动到时,四边形EPFC是正方形.(3)、求证:DE=DF.5. 已知四边形ABCD为菱形,E为对角线AC上的一个动点,连结DE并延长交AB的延长线于点F,连结BE. (1)、如图1,求证:∠AFD=∠EBC.(2)、如图2,若DE=EC且BE⊥AF,求∠DAB的度数.(3)、若∠DAB=90°且当△BEF为等腰三角形时,求∠EFB的度数.(只写出条件与对应的结果)6. 如图,以矩形OABC的顶点О为坐标原点,OA所在直线为x轴,OC所在直线为y轴建立平面直角坐标系.已知OA=2,OC=4,点D为x轴上一动点,以BD为一边在BD右侧作正方形BDEF.
(1)、如图1,求证:∠AFD=∠EBC.(2)、如图2,若DE=EC且BE⊥AF,求∠DAB的度数.(3)、若∠DAB=90°且当△BEF为等腰三角形时,求∠EFB的度数.(只写出条件与对应的结果)6. 如图,以矩形OABC的顶点О为坐标原点,OA所在直线为x轴,OC所在直线为y轴建立平面直角坐标系.已知OA=2,OC=4,点D为x轴上一动点,以BD为一边在BD右侧作正方形BDEF. (1)、若点D与点A重合,请直接写出点E的坐标;(2)、若点D在OA的延长线上,且EA=EB,求点E的坐标.7. 如图,以△ABC的边AB,AC为边作等边三角形ABD和等边三角形ACE,四边形ADFE是平行四边形.
(1)、若点D与点A重合,请直接写出点E的坐标;(2)、若点D在OA的延长线上,且EA=EB,求点E的坐标.7. 如图,以△ABC的边AB,AC为边作等边三角形ABD和等边三角形ACE,四边形ADFE是平行四边形. (1)、当∠BAC满足什么条件时, ADFE是矩形?请说明理由.(2)、当∠BAC满足什么条件时, ADFE不存在?请说明理由.(3)、当△ABC满足什么条件时, ADFE是菱形?当△ABC满足什么条件时, ADFE是正方形?直接给出答案.8. 准备一张矩形纸片,按如图所示的方式操作:将△ABE沿BE翻折,使点A落在对角线BD上的点M处,将△CDF沿DF翻折,使点C落在对角线BD上的点N处.
(1)、当∠BAC满足什么条件时, ADFE是矩形?请说明理由.(2)、当∠BAC满足什么条件时, ADFE不存在?请说明理由.(3)、当△ABC满足什么条件时, ADFE是菱形?当△ABC满足什么条件时, ADFE是正方形?直接给出答案.8. 准备一张矩形纸片,按如图所示的方式操作:将△ABE沿BE翻折,使点A落在对角线BD上的点M处,将△CDF沿DF翻折,使点C落在对角线BD上的点N处. (1)、求证:四边形BFDE是平行四边形.(2)、若四边形BFDE是菱形,AB=2,求菱形BFDE的面积.9. 如图,四边形ABCD为平行四边形,∠BAD的平分线AE交CD于点F,交BC的延长线于点E.
(1)、求证:四边形BFDE是平行四边形.(2)、若四边形BFDE是菱形,AB=2,求菱形BFDE的面积.9. 如图,四边形ABCD为平行四边形,∠BAD的平分线AE交CD于点F,交BC的延长线于点E. (1)、求证:BE=CD.(2)、连结BF,若BF⊥AE,∠E=60°,AB=4,求ABCD的面积。10. 在一元二次方程x2-2ax+b=0中,若a2-b>0,则称a是该方程的中点值.(1)、方程x2-8x+3=0的中点值是.(2)、当a2-b>0时,x1 , x2为方程x2-2ax+b=0的两个根,求证:x2-a=a-x1.(3)、已知x2-mx+n=0的中点值是3,其中一个根是2,求mn的值.11. 在正方形ABCD中,点E、F分别在边BC,CD上,连结AE、AF.
(1)、求证:BE=CD.(2)、连结BF,若BF⊥AE,∠E=60°,AB=4,求ABCD的面积。10. 在一元二次方程x2-2ax+b=0中,若a2-b>0,则称a是该方程的中点值.(1)、方程x2-8x+3=0的中点值是.(2)、当a2-b>0时,x1 , x2为方程x2-2ax+b=0的两个根,求证:x2-a=a-x1.(3)、已知x2-mx+n=0的中点值是3,其中一个根是2,求mn的值.11. 在正方形ABCD中,点E、F分别在边BC,CD上,连结AE、AF. (1)、如图1,过点E作EM⊥AF交AD于点M,求证:AF=EM;(2)、如图2,若AE平分∠BAF,求证:AF=BE+DF.12. 在矩形 中, , ,点 为 上的点,点 矩形内部一动点,连接 , ;
(1)、如图1,过点E作EM⊥AF交AD于点M,求证:AF=EM;(2)、如图2,若AE平分∠BAF,求证:AF=BE+DF.12. 在矩形 中, , ,点 为 上的点,点 矩形内部一动点,连接 , ;

 (1)、如图一,若满足 , , , ,求证: ;(2)、如图二,当点 在线段 上的运动,求 的最小值;(3)、如图三,若点 为 的中点, 为矩形内部一动点,连接 , , ,问 是否有最小值,若有请直接写出答案;若没有,请说明理由.13. 如图,将矩形ABCD绕点顺A时针旋转α°(0°<α<360°),得到矩形AEFG.
(1)、如图一,若满足 , , , ,求证: ;(2)、如图二,当点 在线段 上的运动,求 的最小值;(3)、如图三,若点 为 的中点, 为矩形内部一动点,连接 , , ,问 是否有最小值,若有请直接写出答案;若没有,请说明理由.13. 如图,将矩形ABCD绕点顺A时针旋转α°(0°<α<360°),得到矩形AEFG.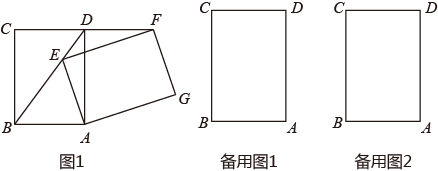 (1)、如图1.当点E在BD上时,
(1)、如图1.当点E在BD上时,①求证:∠BEA=∠BDC;
②连接AF,判断四边形BAFD的形状,并说明理由
(2)、若AB=4,AD= ,当GC=GB时,求ED的长度(画出图形,直接写出结果)14. 我们已经学习了正比例函数 和反比例函数 的图象和性质,下面,我们研究函数 的图象和性质,我们不妨特殊化,设 , ,即 .(1)、① 函数 的自变量x的取值范围是 ▲ ;②容易发现,当 时, ;当 时, .由此可见,图象在第 ▲ 象限;
③阅读材料:当 时, .当 时,即 , 有最小值是2.请仿照上述过程,求出当 时, 的最大值;
(2)、为了画函数 的图象,小明通过列表,描点画出了下图,请连线; (3)、观察图象,当 随着 的增大而增大时,自变量x的取值范围是;(4)、某隧道长185m,一个匀速前进的车队有10辆车,每辆车长4m,相邻两车的距离d(m)与车速v(m/s)的关系式为 ,求自第1辆车车头进隧道至第10辆车车尾出隧道所用时间的最小值.15. 定义:有一组对边平行,有一个内角是它对角的一半的凸四边形叫做半对角四边形,如图1,直线 ,点A,D在直线 上,点B,C在直 上,若∠BAD=2∠BCD,则四边形ABCD是半对角四边形.
(3)、观察图象,当 随着 的增大而增大时,自变量x的取值范围是;(4)、某隧道长185m,一个匀速前进的车队有10辆车,每辆车长4m,相邻两车的距离d(m)与车速v(m/s)的关系式为 ,求自第1辆车车头进隧道至第10辆车车尾出隧道所用时间的最小值.15. 定义:有一组对边平行,有一个内角是它对角的一半的凸四边形叫做半对角四边形,如图1,直线 ,点A,D在直线 上,点B,C在直 上,若∠BAD=2∠BCD,则四边形ABCD是半对角四边形.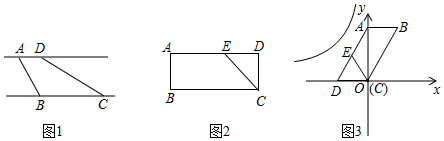 (1)、如图2,点E是矩形ABCD的边AD上一点,AB=1,AE=2.若四边形ABCE为半对角四边形,求AD的长:(2)、如图3,以▱ABCD的顶点C为坐标原点,边CD所在直线为x轴,对角线AC所在直线为y轴,建立平面直角坐标系.点E是边AD上一点,满足BC=AE+CE.求证:四边形ABCE是半对角四边形;(3)、在(2)的条件下,当AB=AE= ,∠B=60°时,将四边形ABCE向左平移a(a>0)个单位后,恰有两个顶点落在反比例函数 的图象上,求k的值.16.(1)、用配方法解一元二次方程除了课本的方法,也可以用下面的配方方式:
(1)、如图2,点E是矩形ABCD的边AD上一点,AB=1,AE=2.若四边形ABCE为半对角四边形,求AD的长:(2)、如图3,以▱ABCD的顶点C为坐标原点,边CD所在直线为x轴,对角线AC所在直线为y轴,建立平面直角坐标系.点E是边AD上一点,满足BC=AE+CE.求证:四边形ABCE是半对角四边形;(3)、在(2)的条件下,当AB=AE= ,∠B=60°时,将四边形ABCE向左平移a(a>0)个单位后,恰有两个顶点落在反比例函数 的图象上,求k的值.16.(1)、用配方法解一元二次方程除了课本的方法,也可以用下面的配方方式:将 两边同时乘以 并移项,得到 ,两边再同时加上 ,得( ▲ )2 .请用这样的方法解方程: ;
(2)、华裔数学家罗博深在2019年提出了一种全新的一元二次方程解法,对于 ,将等式左边进行因式分解,得到以下形式:(从这里可以看出方程的解为 , )
即
因为 ,所以 、 的平均数为 ,不妨设 , ,
利用 ,得 ,所以 ,即能求出 的值.
举例如下:解一元二次方程 ,由于 ,所以方程的两个根为 ,而 ,解得 ,所以方程的解为 , .
请运用以上方法解如下方程① ;②
17. 如图 (1)、如图①,在正方形 中, 的顶点 、 分别在 、 上. 垂足为 且 ,求 的度数.(2)、如图②在 中, , ,点 、 是 上的任意两点,且 ,将 绕点 逆时针旋转 至 位置,连接 ,试判断线段 、 、 之间的数量关系,并说明理由.18. 如图
(1)、如图①,在正方形 中, 的顶点 、 分别在 、 上. 垂足为 且 ,求 的度数.(2)、如图②在 中, , ,点 、 是 上的任意两点,且 ,将 绕点 逆时针旋转 至 位置,连接 ,试判断线段 、 、 之间的数量关系,并说明理由.18. 如图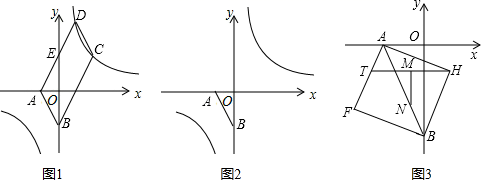
如图1,已知点 , ,且 、 满足 处于平行四边形 的边 与 轴交于点 ,且 为 中点,双曲线 经过 、 两点.
(1)、 , ;(2)、求 点的坐标;(3)、点 在双曲线 上,点 在 轴上(如图2),若以点 、 、 、 为顶点的四边形是平行四边形,请直接写出点 的坐标;(4)、以线段 为对角线作正方形 (如图3),点 是边 上一动点, 是 的中点, ,交 于 ,当 在 上运动时, 的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.19. 如图,在平面直角坐标系中,A (6,0)、B(0, 4)是矩形OACB的两个顶点,双曲线 (k≠0,x>0)经过AC的中点D,点E是矩形OACB与双曲线 的另一个交点,
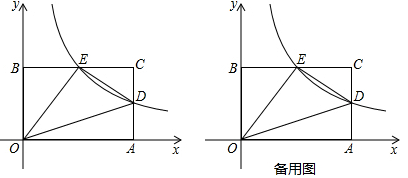 (1)、点D的坐标为 , 点E的坐标为.(2)、动点P在第一象限内,且满足 .
(1)、点D的坐标为 , 点E的坐标为.(2)、动点P在第一象限内,且满足 .①若点P在这个反比例函数的图象上,求点P的坐标;
②连接PO、PE,当PO-PE的值最大时,求点P的坐标;
③若点Q是平面内一点,使得以A、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.
20. 如图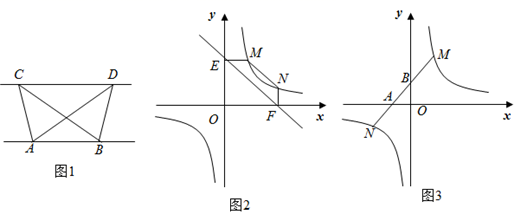 (1)、(探究新知)如图1,已知 与 的面积相等,试判断 与 的位置关系,并说明理由.(2)、(结论应用)如图2,点M,N在反比例函数 的图象上,过点M作 轴,过点N作 轴,垂足分别为E,F.试证明: .(3)、(拓展延伸)若第(2)问中的其他条件不变,只改变点M,N在反比例函数 图象上的位置,如图3所示, 与x轴、y轴分别交于点A、点B,若 ,请求 的长.21. 如图1,矩形 中, , , 为 上一点, 为 延长线上一点,且 .点 从 点出发,沿 方向以 的速度向 运动,连结 、 , 交 于点 .设点 运动的时间为 , 的面积为 ,当 时, 的面积 关于时间 的函数图象如图2所示.
(1)、(探究新知)如图1,已知 与 的面积相等,试判断 与 的位置关系,并说明理由.(2)、(结论应用)如图2,点M,N在反比例函数 的图象上,过点M作 轴,过点N作 轴,垂足分别为E,F.试证明: .(3)、(拓展延伸)若第(2)问中的其他条件不变,只改变点M,N在反比例函数 图象上的位置,如图3所示, 与x轴、y轴分别交于点A、点B,若 ,请求 的长.21. 如图1,矩形 中, , , 为 上一点, 为 延长线上一点,且 .点 从 点出发,沿 方向以 的速度向 运动,连结 、 , 交 于点 .设点 运动的时间为 , 的面积为 ,当 时, 的面积 关于时间 的函数图象如图2所示. (1)、 的长是 ;(2)、当 , 时,求 的值;(3)、如图3,将 沿线段 进行翻折,与 的延长线交于点 ,连结 ,当 为何值时,四边形 为菱形?22. 夏天到了,宁波人最惦记的水果——杨梅进入成熟期,一水果店老板进行杨梅销售,已知杨梅进价为25元/千克.如果售价为30元/千克,那么每天可售出150千克:如果售价为32元/千克,那么每天可售出130千克.经调查发现:每天销售量 (千克)与售价 (元/千克)之间存在一次函数关系.(1)、求出 关于 的一次函数关系式;(2)、若杨梅售价不得高于36元/千克,该店主销售杨梅每天要获得960元的毛利润,则销售单价应定为多少元/千克?(毛利润=销售额-进货成本〉(3)、设杨梅每天销售的毛利润为 元,当杨梅的售价定为多少元/千克时,每天销售获得的毛利润最大?最大毛利润是多少元?23. 如图,在正方形 中, ,E为正方形 内一点, , ,连结 , ,过点D作 ,垂足为点F,交 的延长线于点G,连结 .
(1)、 的长是 ;(2)、当 , 时,求 的值;(3)、如图3,将 沿线段 进行翻折,与 的延长线交于点 ,连结 ,当 为何值时,四边形 为菱形?22. 夏天到了,宁波人最惦记的水果——杨梅进入成熟期,一水果店老板进行杨梅销售,已知杨梅进价为25元/千克.如果售价为30元/千克,那么每天可售出150千克:如果售价为32元/千克,那么每天可售出130千克.经调查发现:每天销售量 (千克)与售价 (元/千克)之间存在一次函数关系.(1)、求出 关于 的一次函数关系式;(2)、若杨梅售价不得高于36元/千克,该店主销售杨梅每天要获得960元的毛利润,则销售单价应定为多少元/千克?(毛利润=销售额-进货成本〉(3)、设杨梅每天销售的毛利润为 元,当杨梅的售价定为多少元/千克时,每天销售获得的毛利润最大?最大毛利润是多少元?23. 如图,在正方形 中, ,E为正方形 内一点, , ,连结 , ,过点D作 ,垂足为点F,交 的延长线于点G,连结 .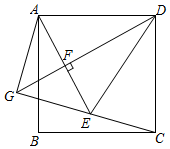 (1)、当 时,求 的度数.(2)、判断 的形状,并说明理由.(3)、当 时,求 的长.24. 如图,四边形 为矩形, , ,线段 上有一动点 ,连接 ,将 沿 折叠到 .
(1)、当 时,求 的度数.(2)、判断 的形状,并说明理由.(3)、当 时,求 的长.24. 如图,四边形 为矩形, , ,线段 上有一动点 ,连接 ,将 沿 折叠到 . (1)、如图①,若 ,当 落在 上时,求 的长;(2)、如图②, 、 、 分别是线段 、 、 的中点,当点 在 边上运动时, 的度数是否会发生变化?若不变,求出这个度数;若变化,请说明理由;(3)、如图③,点 、 ,分别在线段 、 上,连接 、 ,当 时,求 的最小值.25. 如图,将矩形纸片ABCD的四个角向内折叠,恰好拼成一个无缝隙、无重叠的四边形EFGH。
(1)、如图①,若 ,当 落在 上时,求 的长;(2)、如图②, 、 、 分别是线段 、 、 的中点,当点 在 边上运动时, 的度数是否会发生变化?若不变,求出这个度数;若变化,请说明理由;(3)、如图③,点 、 ,分别在线段 、 上,连接 、 ,当 时,求 的最小值.25. 如图,将矩形纸片ABCD的四个角向内折叠,恰好拼成一个无缝隙、无重叠的四边形EFGH。 (1)、求证:四边形EFCH是矩形:(2)、若AH=2,HD=3,求四边形EFCH的面积。26. 我们定义:有一组对边相等,另一组对边不相等的凸四边形叫做“单等对边四边形”。
(1)、求证:四边形EFCH是矩形:(2)、若AH=2,HD=3,求四边形EFCH的面积。26. 我们定义:有一组对边相等,另一组对边不相等的凸四边形叫做“单等对边四边形”。 (1)、如图1,在 ABCD中,点E为AB上不与点A,B重合的一点,CE=CB。
(1)、如图1,在 ABCD中,点E为AB上不与点A,B重合的一点,CE=CB。求证:四边形AECD为单等对边四边形;
(2)、如图2,在8×10的网格中,顶点A、B、C均是格点,请在此网格内找格点D,使四边形ABCD为单等对边四边形,请你在网格中画出所有满足条件的点D;(3)、如图3,在单等对边四边形ABCD中,AB=CD,BC=1,CD=5,∠BCD=90°,若单等对边四边形ABCD内有一点P,使四边形ABCP为平行四边形,且 ABCP与四边形ABCD的面积比为1:3,求 ABCP的面积。27.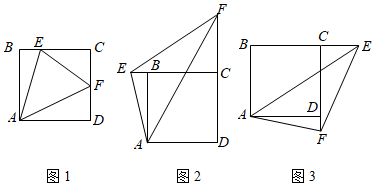 (1)、(发现证明)
(1)、(发现证明)问题:如图1,在正方形ABCD中,点E、F分别是BC、CD边上的动点,且 ,求证: .
观察:EF、DF、BE三条线段都不在同一条直线上,能不能借助图形的运动,将部分线段放置在一条直线上加以证明呢?
思路:将 绕点A顺时针旋转90°使AB与AD重合,得到了旋转后的 .
①根据上述思路在图1中画图分析并证明(写出详细的证明过程).
②若正方形ABCD的边长为6,当动点E在BC边上运动到中点位置时,动点F在CD边上距离D点多长的位置?(写出详细的解答过程)
(2)、(类比迁移)若点E、F分别为正方形两条边的延长线上的动点,EF、BE、DF三者之间还存在(1)中的关系吗?根据解决(1)中问题的经验加以探究.
①如图2,在正方形ABCD中,点E、F分别是CB、DC延长线上的动点,且 ,EF、BE、DF之间的数量关系是什么?请借助图2加以分析,并写出详细的证明过程.
②如图3,在正方形ABCD中,点E、F分别是BC、CD延长线上的动点,且 ,则EF、BE、DF之间的数量关系是 ▲ (直接写出关系式,无需证明).
28. 已知:如图1,函数 和 的图象相交于点 和点 .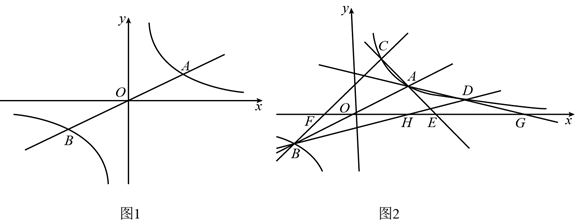 (1)、求点 和点 的坐标(用含 的式子表示);(2)、如图2,点 的坐标为 ,点 是第一象限内函数 的图象上的动点,且在点 的右侧,直线 、 、 、 分别与 轴相交于点 、 、 、 .
(1)、求点 和点 的坐标(用含 的式子表示);(2)、如图2,点 的坐标为 ,点 是第一象限内函数 的图象上的动点,且在点 的右侧,直线 、 、 、 分别与 轴相交于点 、 、 、 .①判定 的形状,并说明理由;
②点 在运动的过程中, 和 的度数和是否变化?如果变化,说明理由;如果不变,求出 和 的度数和.


