高中数学2021-2022高一下学期期末复习题
试卷更新日期:2022-06-10 类型:期末考试
一、单选题
-
1. 已知 , 且 , 则的值为( )A、 B、 C、 D、2. 若复数 满足 ,则 ( )A、1 B、5 C、7 D、253. 如图,测量塔高 ,测量小组选取与塔底 在同一水平面内的两个测量点 和 ,现测得 , , ,在点 处测得塔顶 的仰角为 ,则塔高 为( )
 A、 B、 C、 D、4. 已知 , 则( )A、 B、 C、 D、5. 已知下图中正六边形ABCDEF的边长为4,圆O的圆心为正六边形的中心,直径为2,若点P在正六边形的边上运动,MN为圆O的直径,则的取值范围是( )
A、 B、 C、 D、4. 已知 , 则( )A、 B、 C、 D、5. 已知下图中正六边形ABCDEF的边长为4,圆O的圆心为正六边形的中心,直径为2,若点P在正六边形的边上运动,MN为圆O的直径,则的取值范围是( ) A、 B、 C、 D、6. 已知 , 则( )A、 B、 C、 D、7. 已知 , , 分别为内角 , , 的对边,若 , , 则的值为( )A、1 B、 C、 D、8. 已知是两个不同的平面,l,m是两条不同的直线,有如下四个命题:
A、 B、 C、 D、6. 已知 , 则( )A、 B、 C、 D、7. 已知 , , 分别为内角 , , 的对边,若 , , 则的值为( )A、1 B、 C、 D、8. 已知是两个不同的平面,l,m是两条不同的直线,有如下四个命题:①若 , 则;②若 , 则;③若 , 则﹔④若 , 则 .
其中真命题的个数为( )
A、1个 B、2个 C、3个 D、4个二、多选题
-
9. 要得到如图所示图象,可由图象经过怎样的变换得到( )
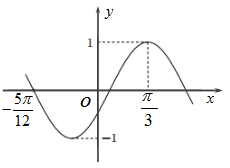 A、每个点横坐标缩短为原来的 , 纵坐标不变,再将横坐标向右平移个单位,纵坐标不变 B、每个点横坐标缩短为原来的 , 纵坐标不变,再将横坐标向右平移个单位,纵坐标不变 C、横坐标向右平移个单位,纵坐标不变,再将每个点横坐标缩短为原来的 , 纵坐标不变 D、横坐标向左平移个单位,纵坐标不变,再将每个点横坐标缩短为原来的 , 纵坐标不变10. 如图,已知正方体 的棱长为2,则下列四个结论正确的是( )
A、每个点横坐标缩短为原来的 , 纵坐标不变,再将横坐标向右平移个单位,纵坐标不变 B、每个点横坐标缩短为原来的 , 纵坐标不变,再将横坐标向右平移个单位,纵坐标不变 C、横坐标向右平移个单位,纵坐标不变,再将每个点横坐标缩短为原来的 , 纵坐标不变 D、横坐标向左平移个单位,纵坐标不变,再将每个点横坐标缩短为原来的 , 纵坐标不变10. 如图,已知正方体 的棱长为2,则下列四个结论正确的是( )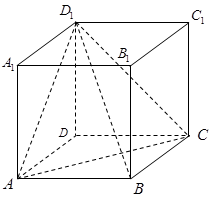 A、直线 与 为异面直线 B、 平面 C、 D、正方体 外接球体积为11. 已知函数 ,则下列说法正确的是( )A、函数 的最小正周期为π B、函数 的对称轴方程为 ( ) C、函数 的图象可由 的图象向右平移 个单位长度得到 D、方程 在[0,10]内有7个根12. 已知向量 , ,则下列说法正确的是( )A、当 时, B、当 时, C、 与 夹角为锐角时,则 的取值范围为 D、当 时, 在 上的投影向量为
A、直线 与 为异面直线 B、 平面 C、 D、正方体 外接球体积为11. 已知函数 ,则下列说法正确的是( )A、函数 的最小正周期为π B、函数 的对称轴方程为 ( ) C、函数 的图象可由 的图象向右平移 个单位长度得到 D、方程 在[0,10]内有7个根12. 已知向量 , ,则下列说法正确的是( )A、当 时, B、当 时, C、 与 夹角为锐角时,则 的取值范围为 D、当 时, 在 上的投影向量为三、填空题
-
13. 已知函数在上的值域为 , 则m的取值范围是 .14. 已知向量 , , 满足 , 则t= .15. 在△ABC中,a,b,c分别是角A,B,C的对边,若a=2,b=3, ,则△ABC外接圆的半径为 .16. 四棱锥中,底面ABCD是矩形,面面ABCD, , , 则四棱锥ABCD的外接球的表面积为 .
四、解答题
-
17. 记 的内角 的对边分别为 ,已知 .(1)、证明: ;(2)、若 ,求 的周长.18. 如图,三棱锥 中, , , , , 是 的中点,点 在线段 上.
 (1)、求证: ;(2)、若 平面 , 求四棱锥 的体积.
(1)、求证: ;(2)、若 平面 , 求四棱锥 的体积.(参考公式:锥体的体积公式 ,其中 是底面积, 是高.)
19. 已知函数 .(1)、求的值;(2)、求的最小正周期和单调递增区间.
