浙江省温州市瑞安市2022年中考二模数学试卷
试卷更新日期:2022-06-10 类型:中考模拟
一、单选题
-
1. 在﹣3,﹣1,0,2这四个数中,最小的数是( )A、﹣3 B、﹣1 C、0 D、22. 截至今年2月份,温州全市接种新冠疫苗已超21000000剂次.数据21000000用科学记数法表示为( )A、210×105 B、21×106 C、2.1×107 D、0.21×1083. 如图所示的几何体的主视图是( )
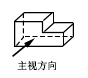 A、
A、 B、
B、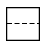 C、
C、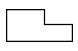 D、
D、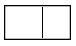 4. 计算 的结果是( )A、 B、 C、 D、5. 一个不透明布袋里装有只有颜色不同的5个球,其中2个红球,3个白球,从中任意摸出一个球,是红球的概率是( )A、 B、 C、 D、6. 如图,已知△ABC与△DEF是位似图形,O是位似中心,若OA=2OD,则△ABC与△DEF的周长之比是( )
4. 计算 的结果是( )A、 B、 C、 D、5. 一个不透明布袋里装有只有颜色不同的5个球,其中2个红球,3个白球,从中任意摸出一个球,是红球的概率是( )A、 B、 C、 D、6. 如图,已知△ABC与△DEF是位似图形,O是位似中心,若OA=2OD,则△ABC与△DEF的周长之比是( )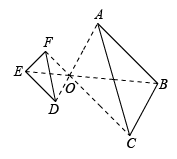 A、2:1 B、3:1 C、4:1 D、6:17. 若m千克的某种糖果售价为n元,则8千克的这种糖果售价为( )A、 元 B、 元 C、 元 D、 元8. 某村计划挖一条引水渠,渠道的横断面ABCD是一个轴对称图形(如图所示).若渠底宽BC为2m,渠道深BH为3m,渠壁CD的倾角为 ,则渠口宽AD为( )
A、2:1 B、3:1 C、4:1 D、6:17. 若m千克的某种糖果售价为n元,则8千克的这种糖果售价为( )A、 元 B、 元 C、 元 D、 元8. 某村计划挖一条引水渠,渠道的横断面ABCD是一个轴对称图形(如图所示).若渠底宽BC为2m,渠道深BH为3m,渠壁CD的倾角为 ,则渠口宽AD为( )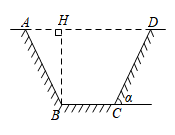 A、( )m B、( )m C、( )m D、( )m9. 已知抛物线 与 轴交于A,B两点,P为抛物线顶点,且当 时,y随 的增大而减小,若△ABP为等边三角形,则 的值为( )A、 B、 C、 D、10. 如图,在△ABC中,∠ACB=90°, 分别以AC, BC为边向外作正方形ACDE与正方形BCFG, H为EG的中点,连接DH,FH.记△FGH的面积为S1 , △CDH的面积为S2 , 若S1-S2=6,则AB的长为( )
A、( )m B、( )m C、( )m D、( )m9. 已知抛物线 与 轴交于A,B两点,P为抛物线顶点,且当 时,y随 的增大而减小,若△ABP为等边三角形,则 的值为( )A、 B、 C、 D、10. 如图,在△ABC中,∠ACB=90°, 分别以AC, BC为边向外作正方形ACDE与正方形BCFG, H为EG的中点,连接DH,FH.记△FGH的面积为S1 , △CDH的面积为S2 , 若S1-S2=6,则AB的长为( )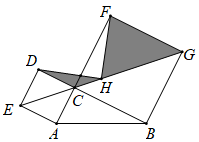 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 因式分解: .12. 不等式组 的解为.13. 如图是某校七年级学生参加课外兴趣小组人数的扇形统计图,若参加书法兴趣小组的人数是30人,则参加绘画兴趣小组的人数是人.
 14. 已知扇形的面积为3π,圆心角为120°,则它的半径为 .15. 如图,点A在反比例函数 (k>0, x>0)的图象上,AB⊥y轴于点B,C为x轴正半轴上一点,将△ABC绕点A旋转180°得到△AED,点C的对应点D恰好落在函数图象上.若△BOC的面积为6,则k的值为.
14. 已知扇形的面积为3π,圆心角为120°,则它的半径为 .15. 如图,点A在反比例函数 (k>0, x>0)的图象上,AB⊥y轴于点B,C为x轴正半轴上一点,将△ABC绕点A旋转180°得到△AED,点C的对应点D恰好落在函数图象上.若△BOC的面积为6,则k的值为. 16. 如图1的螺丝钉由头部(直六棱柱)和螺纹(圆螺纹直径柱)组合而成,其俯视图如图2所示.小明想用一把刻度尺测量出螺纹直径.已知刻度尺紧靠螺纹,经过点A且交CD于点P,若测得AP长为头部13mm,正六边形ABCDEF的边长为7.5mm,则CP长为mm, 螺纹直径为 mm.
16. 如图1的螺丝钉由头部(直六棱柱)和螺纹(圆螺纹直径柱)组合而成,其俯视图如图2所示.小明想用一把刻度尺测量出螺纹直径.已知刻度尺紧靠螺纹,经过点A且交CD于点P,若测得AP长为头部13mm,正六边形ABCDEF的边长为7.5mm,则CP长为mm, 螺纹直径为 mm.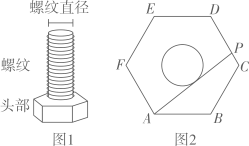
三、解答题
-
17.(1)、计算: .(2)、化简: .18. 如图,AE平分∠BAC, AC=CE.
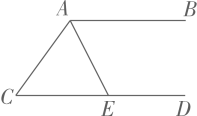 (1)、求证:AB∥CD.(2)、若∠C=50°,求∠AED的度数.19. 为了解某校七年级450名男生引体向上成绩情况,陈老师对该校随机抽取的30名七年级男生进行了引体向上测试,制成统计表如下:
(1)、求证:AB∥CD.(2)、若∠C=50°,求∠AED的度数.19. 为了解某校七年级450名男生引体向上成绩情况,陈老师对该校随机抽取的30名七年级男生进行了引体向上测试,制成统计表如下:成绩(个)
0
1
2
3
4
5
6
7
学生(人)
1
3
5
6
4
5
3
3
(1)、求这30名男生引体向上成绩的平均数、中位数和众数.(2)、学校规定:当引体向上测试成绩超过5个时成绩等级评为优秀,请估计该校七年级所有男生引体向上成绩为优秀的人数.20. 如图,在8×8的方格纸中,每个小正方形的边长均为1,四边形ABCD为格点图形(顶点在格点上),请按以下要求画出相应的格点图形.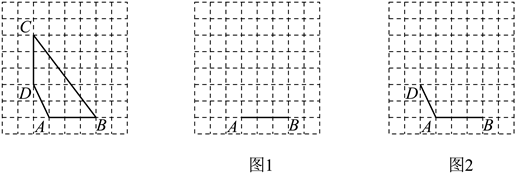 (1)、在图1中画出格点△ABP,使△ABP的面积等于四边形ABCD的面积.(2)、在图2中画出格点四边形ABQD,使四边形ABQD的面积等于四边形ABCD的面积,且格点Q不与格点C重合.21. 已知抛物线y=x2 +bx+c经过点A(4,3),B(-1,8),与y轴交于点C.(1)、求抛物线的函数表达式.(2)、把点C向下平移m(m>0)个单位得到点M.若点M向右平移n(n>0)个单位,将与该抛物线上的点P重合;若点M向右平移(n+3)个单位,将与该抛物线上的点Q重合,求m,n的值.22. 如图,△ABC内接于 , AB为直径,∠ACB 的平分线分别交AB于点D.交 于点E,过点E作 的切线,交CE的平行线AF于点F.
(1)、在图1中画出格点△ABP,使△ABP的面积等于四边形ABCD的面积.(2)、在图2中画出格点四边形ABQD,使四边形ABQD的面积等于四边形ABCD的面积,且格点Q不与格点C重合.21. 已知抛物线y=x2 +bx+c经过点A(4,3),B(-1,8),与y轴交于点C.(1)、求抛物线的函数表达式.(2)、把点C向下平移m(m>0)个单位得到点M.若点M向右平移n(n>0)个单位,将与该抛物线上的点P重合;若点M向右平移(n+3)个单位,将与该抛物线上的点Q重合,求m,n的值.22. 如图,△ABC内接于 , AB为直径,∠ACB 的平分线分别交AB于点D.交 于点E,过点E作 的切线,交CE的平行线AF于点F.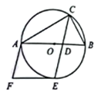 (1)、求证:四边形ADEF为平行四边形.(2)、若tan∠CAB= ,AF=5,求四边形ADEF的面积.23. 2022年中国航天在诸多领域实现重大突破,在全国掀起航天知识学习的浪潮.某校40名同学要去参观航天展览馆,已知展览馆分A、B、C三个场馆,且购买2张 场馆门票和1张 场馆门票共需要140元,购买3张 场馆门票和2张 场馆门票共需要230元.由于场地和疫情原因,要求到 场馆参观的人数要少于到 场馆参观的人数,且每一位同学只能选择一个场馆参观.(1)、求 场馆和 场馆门票的单价.(2)、已知 场馆门票每张售价15元,且参观当天有优惠活动;每购买1张 场馆门票就赠送1张 场馆门票.
(1)、求证:四边形ADEF为平行四边形.(2)、若tan∠CAB= ,AF=5,求四边形ADEF的面积.23. 2022年中国航天在诸多领域实现重大突破,在全国掀起航天知识学习的浪潮.某校40名同学要去参观航天展览馆,已知展览馆分A、B、C三个场馆,且购买2张 场馆门票和1张 场馆门票共需要140元,购买3张 场馆门票和2张 场馆门票共需要230元.由于场地和疫情原因,要求到 场馆参观的人数要少于到 场馆参观的人数,且每一位同学只能选择一个场馆参观.(1)、求 场馆和 场馆门票的单价.(2)、已知 场馆门票每张售价15元,且参观当天有优惠活动;每购买1张 场馆门票就赠送1张 场馆门票.①若购买 场馆门票赠送的 场馆门票刚好够参观 场馆的同学使用,求此次购买门票所需总金额的最小值.
②若参观 场馆的同学除了使用掉赠送的门票外,还需另外购买部分门票,且最终购买三种门票共花费了1200 元,求所有满足条件的购买方案.
24. 如图,在等边△ABC中,AB=6,D为边BC上一点,以AD为边向右构造等边△ADE,过点A作AF⊥DE于点F,并延长交BC于点G,连接CE.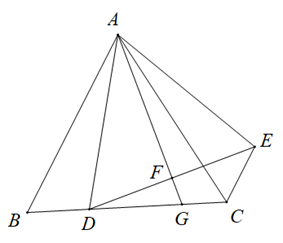 (1)、求证:BD=CE.(2)、当 时,求CE的长.(3)、已知BD=2, P为边AC的中点,Q为线段AG上一点,当直线PQ将△ACD的面积分成1:3两部分时,求 的值.
(1)、求证:BD=CE.(2)、当 时,求CE的长.(3)、已知BD=2, P为边AC的中点,Q为线段AG上一点,当直线PQ将△ACD的面积分成1:3两部分时,求 的值.