浙江省杭州市拱墅区2022年九年级中考一模数学试卷
试卷更新日期:2022-06-10 类型:中考模拟
一、单选题
-
1. 在-4,5,0,-1这四个数中,最小的数是( )A、-4 B、5 C、0 D、-12. ( )A、 B、 C、 D、3. 在北京冬奥会期间,约19000名赛会志愿者用出色的服务,为奥运盛会的顺利举行提供了重要保障.数据19000用科学记数法可表示为( )A、 B、 C、 D、4. 如图,直线AB,CD相交于点O,OE平分 .若 ,则 的度数为( )
 A、 B、 C、 D、5. 在地球表面以下,每下降1km温度就上升约10℃.某日地表温度是18℃,地下某处A的温度是25℃.设A处在地表以下x千米,则( )A、 B、 C、 D、6. 小皓在计算一组较大的数据的平均数和方差时,他先将原数据中的每一个数都减去某个相同的正数,然后对所得的新数据进行统计分析.新数据与原数据相比,( )A、平均数不变,方差不变 B、平均数变大,方差变大 C、平均数变小,方差不变 D、平均数变小,方差变小7. 已知点 , 都在反比例函数 的图象上,( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则8. 已知AB是 的弦,半径 于点D,若 , ,则 的半径为( )A、 B、 C、 D、9. 如图,在 中, ,以点A为圆心,AC的长为半径作弧交AB于点D,连接DC;再以点D为圆心,DC的长为半径作弧交CB的延长线于点E.若 , ,则( )
A、 B、 C、 D、5. 在地球表面以下,每下降1km温度就上升约10℃.某日地表温度是18℃,地下某处A的温度是25℃.设A处在地表以下x千米,则( )A、 B、 C、 D、6. 小皓在计算一组较大的数据的平均数和方差时,他先将原数据中的每一个数都减去某个相同的正数,然后对所得的新数据进行统计分析.新数据与原数据相比,( )A、平均数不变,方差不变 B、平均数变大,方差变大 C、平均数变小,方差不变 D、平均数变小,方差变小7. 已知点 , 都在反比例函数 的图象上,( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则8. 已知AB是 的弦,半径 于点D,若 , ,则 的半径为( )A、 B、 C、 D、9. 如图,在 中, ,以点A为圆心,AC的长为半径作弧交AB于点D,连接DC;再以点D为圆心,DC的长为半径作弧交CB的延长线于点E.若 , ,则( ) A、 B、 C、 D、10. 设函数 (a是实数),当 时,对应的函数值分别为r,s,t,下列选项中正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则
A、 B、 C、 D、10. 设函数 (a是实数),当 时,对应的函数值分别为r,s,t,下列选项中正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则二、填空题
-
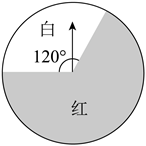
11. 因式分解: .12. 若扇形的圆心角为 ,半径为6,则这个扇形的弧长为(结果保留π).13. 满足不等式 的负整数可以是(写出一个即可).14. 如图是一个可以自由转动的两色转盘,其中白色扇形和红色扇形的圆心角分别为 和 .若让转盘自由转动一次,则指针落在白色区域的概率是.若让转盘自由转动两次,则指针一次落在白色区域,另一次落在红色区域的概率是.
 15. 如图,AB是 的直径,点P是AB延长线上的一点,PC是 的切线,C为切点,若 , ,则PC=.
15. 如图,AB是 的直径,点P是AB延长线上的一点,PC是 的切线,C为切点,若 , ,则PC=. 16. 图是一张矩形纸片ABCD,点E在AB边上,把 沿直线DE折叠,使点A落在BC边上的点F处,点G在BC边上,把 沿直线DG折叠,使点C恰好落在线段DF上的点H处, .若 ,则 .
16. 图是一张矩形纸片ABCD,点E在AB边上,把 沿直线DE折叠,使点A落在BC边上的点F处,点G在BC边上,把 沿直线DG折叠,使点C恰好落在线段DF上的点H处, .若 ,则 .
三、解答题
-
17. 计算:(1)、 ;(2)、 .18. 为了解某校七年级学生100m跑成绩(精确到0.1秒),对该年级全部学生进行100m跑测试,把测得的数据分成五组,绘制成如图所示的频数表和未完成的频数直方图(每组不含前一个边界值,含后一个边界值).
某校七年级全部学生100m跑成绩的频数表
组别(秒)
频数
12.5~13.5
32
13.5~14.5
14.5~15.5
112
15.5~16.5
a
16.5~17.5
32
某校七年级全部学生100m跑成绩的频数直方图
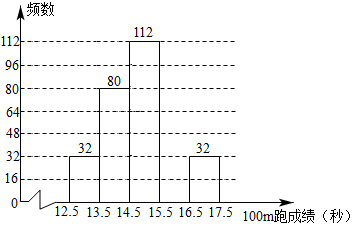 (1)、求该年级学生的总人数(2)、把频数直方图补充完整.(3)、求该年级100m跑成绩不超过15.5秒的学生数占该年级全部学生数的百分比.19. 问题:如图,在 中,点E,点F在对角线AC上(不与点A,点C重合),连接BE,DF.若▲ , 求证: .在① ,② ,③ 这三个条件中选择其中一个,补充在上面问题中,并完成问题的解答.
(1)、求该年级学生的总人数(2)、把频数直方图补充完整.(3)、求该年级100m跑成绩不超过15.5秒的学生数占该年级全部学生数的百分比.19. 问题:如图,在 中,点E,点F在对角线AC上(不与点A,点C重合),连接BE,DF.若▲ , 求证: .在① ,② ,③ 这三个条件中选择其中一个,补充在上面问题中,并完成问题的解答.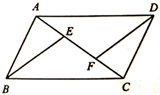 20. 小明和小军在一条直道上由西向东匀速行走,小明以每分钟60米的速度从A地出发,小军同时以每分钟v米的速度从A地东边80米的B地出发,小明和小军离A地的距离y(米)与行走时间x(分钟)的关系如图.
20. 小明和小军在一条直道上由西向东匀速行走,小明以每分钟60米的速度从A地出发,小军同时以每分钟v米的速度从A地东边80米的B地出发,小明和小军离A地的距离y(米)与行走时间x(分钟)的关系如图. (1)、求小军离A地的距离y(米)与行走时间x(分钟)的函数表达式.(2)、当小明到达离A地720米的C地时,小军离C地还有多少米?21. 图,在 中, 于点D,点E在AB上(不与点A,点B重合),连接CE交AD于点F, .
(1)、求小军离A地的距离y(米)与行走时间x(分钟)的函数表达式.(2)、当小明到达离A地720米的C地时,小军离C地还有多少米?21. 图,在 中, 于点D,点E在AB上(不与点A,点B重合),连接CE交AD于点F, .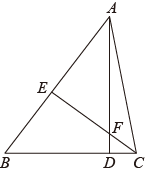 (1)、求证: .(2)、若 , , ,求 的面积.
(1)、求证: .(2)、若 , , ,求 的面积.
