四川省德阳市旌阳区2022年九年级第二次模拟考试数学试卷

试卷更新日期：2022-06-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，最小的数是（）

A、2 B、0 C、 $- 1$ D、 $| - 3 |$

查看试题解析
2. 已知某种细胞的直径约为 $2.13 \times 10^{- 4}$ cm，请问 $2.13 \times 10^{- 4}$ 这个数原来的数是（）

A、21300 B、2130000 C、0.0213 D、0.000213

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{5} + \sqrt{3} = \sqrt{8}$ B、 $\sqrt{4} \div \sqrt{2} = 2$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 ${(- \sqrt{2})}^{2} = - 2$

查看试题解析
4. 一把直尺和一块直角三角尺（含30°、60°角）如图所示摆放，直尺的一边与三角尺的两直角边BC、AC分别交于点D、点E，直尺的另一边过A点且与三角尺的直角边BC交于点F，若∠CAF＝42°，则∠CDE度数为（）

A、62° B、48° C、58° D、72°

查看试题解析
5. 在国家“双减”政策背景下，我区某学校为了解九年级620名学生的睡眠情况，抽查了其中的100名学生的睡眠时间进行统计，下面叙述中，正确的是（）.

A、以上调查属于全面调查 B、620是样本容量 C、100名学生是总体的一个样本 D、每名学生的睡眠时间是一个个体

查看试题解析
6. 如图，四边形ABCD是平行四边形，下列结论中错误的是（）

A、当▱ABCD是矩形时，∠ABC＝90° B、当▱ABCD是菱形时，AC⊥BD C、当▱ABCD是正方形时，AC＝BD D、当▱ABCD是菱形时，AB＝AC

查看试题解析
7. 筒车是我国古代发明的一种水利灌溉工具，如图1，筒车盛水桶的运行轨道是以轴心O为圆心的圆，如图2，已知圆心O在水面上方，且 $⊙ O$ 被水面截得弦 $A B$ 长为4米， $⊙ O$ 半径长为3米.若点C为运行轨道的最低点，则点C到弦 $A B$ 所在直线的距离是（）

A、1米 B、2米 C、 $(3 - \sqrt{5})$ 米 D、 $(3 + \sqrt{5})$ 米

查看试题解析
8. 如图，在Rt△ABC中，∠B＝90°，AB＝8，BC＝6，延长BC至E，使得CE＝BC，将△ABC沿AC翻折，使点B落点D处，连接DE，则DE的长为（）

A、 $\frac{18}{5}$ B、 $\frac{24}{5}$ C、 $\frac{32}{5}$ D、 $\frac{36}{5}$

查看试题解析
9. 一个几何体的三视图如下：其中主视图和左视图都是腰长为4，底边为2的等腰三角形，则这个几何体侧面展开图的面积和圆心角分别是（）

A、4π60° B、4π90° C、2π90° D、8π60°

查看试题解析
10. 如图，在△ABC中，BC=3，点D为AC延长线上的一点，AC=3CD，过点D作DH $//$ AB，交BC的延长线于点H，若∠CBD=∠A，则AB的长为（）

A、6 B、5 C、4 D、4.2

查看试题解析
11. 如图，在矩形ABDC中，AC=4cm，AB=3cm，点E以0.5cm/s的速度从点B到点C，同时点F以0.4cm/s的速度从点D到点B，当一个点到达终点时，则运动停止，点P是边CD上一点，且CP=1，且Q是线段EF的中点，则线段QD+QP的最小值为（）

A、 $2 \sqrt{5}$ B、5 C、 $\sqrt{17}$ D、 $\sqrt{34}$

查看试题解析
12. 如图， $△ O A_{1} B_{1}$ ， $△ A_{1} A_{2} B_{2}$ ， $△ A_{2} A_{3} B_{3}$ ，……是分别以 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ，……为直角顶点，一条直角边在 $x$ 轴正半轴上的等腰直角三角形，其斜边的中点 $C_{1} (x_{1} ， y_{1})$ ， $C_{2} (x_{2} ， y_{2})$ ， $C_{3} (x_{3} ， y_{3})$ ，……，均在反比例函数 $y = \frac{4}{x} (x > 0)$ 的图象上，则 $y_{1} + y_{2} + \dots \dots + y_{2022}$ 的值为（）

A、 $2 \sqrt{2021}$ B、 $2 \sqrt{2022}$ C、 $4 \sqrt{2021}$ D、 $4 \sqrt{2022}$

查看试题解析

二、填空题

13. 若分式 $\frac{x + 2}{x^{2} - 4}$ 有意义，则x的取值范围为．

查看试题解析
14. 已知a，b，c是△ABC的三边的长，且满足2a²+b²+c²-2a（b+c）=0，则△ABC的形状为三角形.

查看试题解析
15. 如图，⊙O是正五边形ABCDE的外接圆，点P为ED上的一点，则∠APC的度数为．

查看试题解析
16. 如图，坡面CD的坡比为 $1 ： \sqrt{3}$ ，坡顶的平地BC上有一棵小树AB，当太阳光线与水平线夹角成60°时，测得小树的在坡顶平地上的树影BC=3米，斜坡上的树影CD= $\sqrt{3}$ 米，则小树AB的高是.

查看试题解析
17. 如图，点C在线段 $A B$ 上，且 $A C = 2 B C$ ，分别以 $A C$ 、 $B C$ 为边在线段 $A B$ 的同侧作正方形 $A C D E$ 、 $B C F G$ ，连接 $E C$ 、 $E G$ ，则sin∠CEG=.

查看试题解析
18. 抛物线 $y = a x^{2} + b x + c$ （ $a \neq 0$ ）的对称轴为 $x = - 1$ ，经过点（1，n），顶点为P，下列四个结论：
①若 $a < 0$ ，则 $c > n$ ；

②若c与n异号，则抛物线与x轴有两个不同的交点；

③方程 $a x^{2} + (b - n) x + c = 0$ 一定有两个不相等的实数解；

④设抛物线交y轴于点C，不论a为何值，直线PC始终过定点（3，n）.

其中正确的是（填写序号）.

查看试题解析

三、解答题

19. 计算： ${(- 2)}^{2} + \sqrt{{(- 3)}^{2}} - \sqrt[3]{27} + | \sqrt{3} - 2 | + {(- \frac{1}{2})}^{- 1}$ .

查看试题解析
20. 我区某学校根据《成都市中小学生课后服务实施意见》，积极开展课后延时服务活动，提供了“器乐，体锻，科创，书法，美术，课本剧，棋类……”等课程供学生自由选择，半学期后，该校为了解学生对课后延时服务的满意情况，随机对部分学生进行问卷调查，并将调查结果按照“A．满意；B．比较满意；C．基本满意；D．不满意”四个等级绘制成如图所示的两幅不完整统计图．

请根据图中信息，解答下列问题：

(1)、将条形统计图补充完整；

(2)、表示等级C的扇形的圆心角是度；

(3)、由于学校条件限制，“科创”课程仅剩下一个名额，而学生小华和小亮都想参加，他们决定采用抽纸牌的方法来确定，规则是：“将背面完全相同，正面分别标有数字1，2，3，4的四张牌洗匀后，背面朝上放置在桌面上，每人随机抽一次且一次只抽一张；一人抽后记下数字，将牌放回洗匀背面朝上放置在桌面上，再由另一人抽．若小华抽得的数字比小亮抽得的数字大，名额给小华，否则给小亮．”请用画树状图或列表的方法计算出小华和小亮获得该名额的概率，并说明这个规则对双方是否公平．

查看试题解析
21. 如图，在四边形ABCD中，AB ∥ DC，AB＝AD，对角线AC，BD交于点O，AC平分∠BAD，过点C作CE⊥AB交AB的延长线于点E，连接OE

(1)、求证：四边形ABCD是菱形；

(2)、若AB＝ $\sqrt{10}$ ，BD＝2，求 $△$ OBE的面积.

查看试题解析
22. 已知反比例函数 $y = \frac{k}{2 x}$ 和一次函数y＝2x+b，其中一次函数的图象经过点A（﹣1，﹣3）和B（1，m）.反比例函数图象经过点B.

(1)、求反比例函数的解析式和一次函数的解析式；

(2)、若直线 $y = - x + \frac{1}{2}$ 交x轴于C，交y轴于D，点P为反比例函数 $y = \frac{k}{2 x}$ （x＞0）的图象上一点，过P作y轴的平行线交直线CD于E，过P作x轴的平行线交直线CD于F，
①请问：在该反比例函数图象上是否存在点P，使△PFE≌△OCD？若存在，求点P的坐标；若不存在，请说明理由.

②求证：DE•CF为定值.

查看试题解析
23. 如图，在平面直角坐标系中，抛物线y $= - \frac{1}{2} x^{2} +$ bx+c与x轴交于A（﹣2，0）、B（4，0）两点（点A在点B的左侧），与y轴交于点C，连接AC、BC，点P为直线BC上方抛物线上一动点，连接OP交BC于点Q．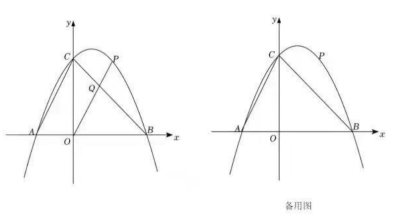

(1)、求抛物线的函数表达式；

(2)、当 $\frac{P Q}{O Q}$ 的值最大时，求点P的坐标和 $\frac{P Q}{O Q}$ 的最大值；

(3)、把抛物线y $= - \frac{1}{2} x^{2} +$ bx+c沿射线AC方向平移 $\sqrt{5}$ 个单位得新抛物线y'，M是新抛物线上一点，N是新抛物线对称轴上一点，当以M、N、B、C为顶点的四边形是平行四边形时，直接写出N点的坐标．

查看试题解析