四川省成都市新都区2022年中考第二次诊断性考试数学试卷
试卷更新日期:2022-06-10 类型:中考模拟
一、单选题
-
1. 的绝对值是( )A、 B、 C、2022 D、2. 计算 的结果等于( )A、10 B、 C、50 D、203. 2022年4月16日,在中国空间站生话工作了六个月的三位航天员翟志刚,王亚平,叶光富乘坐神舟十三号载人飞船成功返回地球,这标志着我国空间站关键技术验证阶段即将圆满收官.神舟十三号在太空中平均飞行速度约为每小时28000千米.将28000用科学记数法表示是( )A、 B、 C、 D、4. 实数a,b在数轴上的对应点的位置如图所示,下列结论中不正确的是( )
 A、 B、 C、 D、5. 三根等长的木杆竖直地立在平地的同一个圆周上,圆心处有一盏灯光,其俯视图如图所示,图中画出了其中一根木杆在灯光下的影子.下列四幅图中正确画出另两根木杆在同一灯光下的影子的是( )
A、 B、 C、 D、5. 三根等长的木杆竖直地立在平地的同一个圆周上,圆心处有一盏灯光,其俯视图如图所示,图中画出了其中一根木杆在灯光下的影子.下列四幅图中正确画出另两根木杆在同一灯光下的影子的是( ) A、
A、 B、
B、 C、
C、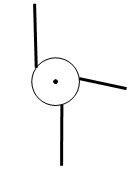 D、
D、 6. 如图,四边形 内接于 ,点E为 边上任意一点(点E不与点B,C重合),连接 ,若 ,则 的度数可能是( )
6. 如图,四边形 内接于 ,点E为 边上任意一点(点E不与点B,C重合),连接 ,若 ,则 的度数可能是( ) A、 B、 C、 D、7. 随着防疫工作的推进和宣传工作的深入,人们对接种新冠疫苗越来越重视.小聪想利用折线统计图反映所在社区去年下半年每月新冠疫苗接种人次的变化情况,以下是打乱的统计步骤:①按统计表的数据绘制折线统计图;②整理社区每月接种人次的数据并制作统计表;③从社区办事处收集去年下半年新冠疫苗接种人次的数据;④从折线统计图中分析该社区去年下半年每月新冠疫苗接种人次的变化趋势.正确统计步骤的顺序是( )A、①→②→③→④ B、③→②→①→④ C、③→①→②→④ D、②→④→③→①8. 如图,在直角坐标系的x轴负半轴和y轴正半轴上分别截取OA,OB,使OA=OB,再分别以点A,B为圆心,以大于 AB长为半径作弧,两弧交于第二象限的点N,若点N的坐标为(2-n,2n-6),则n的值是( )
A、 B、 C、 D、7. 随着防疫工作的推进和宣传工作的深入,人们对接种新冠疫苗越来越重视.小聪想利用折线统计图反映所在社区去年下半年每月新冠疫苗接种人次的变化情况,以下是打乱的统计步骤:①按统计表的数据绘制折线统计图;②整理社区每月接种人次的数据并制作统计表;③从社区办事处收集去年下半年新冠疫苗接种人次的数据;④从折线统计图中分析该社区去年下半年每月新冠疫苗接种人次的变化趋势.正确统计步骤的顺序是( )A、①→②→③→④ B、③→②→①→④ C、③→①→②→④ D、②→④→③→①8. 如图,在直角坐标系的x轴负半轴和y轴正半轴上分别截取OA,OB,使OA=OB,再分别以点A,B为圆心,以大于 AB长为半径作弧,两弧交于第二象限的点N,若点N的坐标为(2-n,2n-6),则n的值是( ) A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
9. 计算: =10. 关于x的方程x2+kx-14=0的两根是7和-2,则k的值是.11. 有一个容积为2升的圆柱形开口空瓶,小明以0.8升/秒的速度匀速向空瓶注水,注满后停止,等3秒后,再以1升/秒的速度匀速倒空瓶中的水,设所用时间为x秒,瓶内水的体积为y升,y与x的函数关系图象如图所示,则图中 ; .
 12. 小颖在一本书上看到一个风筝模型,形状如图所示,其中对角线 ,并且两条对角线长分别为 和 .现在小颖照着模型按照1:3的比例放大制作一个大风筝,制作风筝需要彩色纸覆盖,而彩色纸是从一张刚好覆盖整个风筝的矩形彩色纸(如图中虚线所示)裁剪下来的,那么从四个角裁剪下来废弃不用的彩色纸的面积是 .
12. 小颖在一本书上看到一个风筝模型,形状如图所示,其中对角线 ,并且两条对角线长分别为 和 .现在小颖照着模型按照1:3的比例放大制作一个大风筝,制作风筝需要彩色纸覆盖,而彩色纸是从一张刚好覆盖整个风筝的矩形彩色纸(如图中虚线所示)裁剪下来的,那么从四个角裁剪下来废弃不用的彩色纸的面积是 . 13. 如图,四边形ABCD由两个直角三角形构成,已知AD=CD,tanα= ,则tanβ=.
13. 如图,四边形ABCD由两个直角三角形构成,已知AD=CD,tanα= ,则tanβ=. 14. 将点 先向右移动a个单位,再向上移动b个单位后落在直线 上,则代数式 的值为.15. 关于x的方程 的解为正数,则a的取值范围为.16. 刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”利用圆的内接正多边形逐步逼近圆来近似计算圆的面积,他从正六边形开始分割圆,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形……割的越细,圆的内接正多边形就越接近圆.如图,若用圆的内接正十二边形的面积S1 , 来近似估计⊙O的面积S,设正十二边形边长为1,则S1=; .
14. 将点 先向右移动a个单位,再向上移动b个单位后落在直线 上,则代数式 的值为.15. 关于x的方程 的解为正数,则a的取值范围为.16. 刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”利用圆的内接正多边形逐步逼近圆来近似计算圆的面积,他从正六边形开始分割圆,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形……割的越细,圆的内接正多边形就越接近圆.如图,若用圆的内接正十二边形的面积S1 , 来近似估计⊙O的面积S,设正十二边形边长为1,则S1=; . 17. 将一副三角板中的两个三角板的两条直角边重合叠放在一起,三角板 固定不动,三角板 绕直角顶点O按顺时针或逆时针方向任意转动一个角 ,如图所示,当这两块三角板各有一条边互相垂直时,在 , , , , , , 这七个度数中是 的度数的概率为.
17. 将一副三角板中的两个三角板的两条直角边重合叠放在一起,三角板 固定不动,三角板 绕直角顶点O按顺时针或逆时针方向任意转动一个角 ,如图所示,当这两块三角板各有一条边互相垂直时,在 , , , , , , 这七个度数中是 的度数的概率为.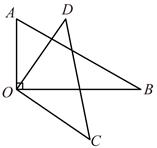 18. 如图,在矩形 中, ,点E,F分别是 的中点, 是等边三角形, 于点H,交 于点P,交 延长线于K.下列结论:① ;② ;③ ;④ .其中正确结论的序号是.
18. 如图,在矩形 中, ,点E,F分别是 的中点, 是等边三角形, 于点H,交 于点P,交 延长线于K.下列结论:① ;② ;③ ;④ .其中正确结论的序号是.
三、解答题
-
19.(1)、计算:(2)、先化简,再求值: ,其中 .20. 在课堂上,同学们已经学习了一些测量距离的方法.小刚想尝试利用无人机测量新都的母亲河——毗河某一处的宽度.如图所示,小刚站在河岸一侧的D点操控无人机,操纵器距地面距离DE=1.5米,在河对岸安放了一标志物F点,无人机在点D正上方的点A,距离地面的飞行高度AD是57.5米,匀速水平飞行4秒到达点B,此时,小刚手里的操纵器测量无人机的仰角为63°,然后无人机又继续以同样的速度水平飞行12秒到达点C,测得点F的俯角为45°(点A,B,C,D,E,F在同一平面内).(参考数据:sin63°≈0.90,cos63°≈0.45,tan63°≈2.00)
 (1)、求无人机飞行的速度是多少米/秒:(2)、求河宽DF的距离.21. 2022年是中国共青团建团100周年,某学校组织学生开展庆祝建团100年的文艺作品征集活动,作品形式有A:绘画:B:书法:C:征文这三种类型,每个学生选择一种作品类型完成,根据某班学生完成作品的类型和数据,绘制成如图所示的条形统计图和扇形统计图.
(1)、求无人机飞行的速度是多少米/秒:(2)、求河宽DF的距离.21. 2022年是中国共青团建团100周年,某学校组织学生开展庆祝建团100年的文艺作品征集活动,作品形式有A:绘画:B:书法:C:征文这三种类型,每个学生选择一种作品类型完成,根据某班学生完成作品的类型和数据,绘制成如图所示的条形统计图和扇形统计图. (1)、根据图中信息,回答下列问题:
(1)、根据图中信息,回答下列问题:① , ;
②补全条形统计图;
(2)、如果小红和小明每人随机选择一种作品类型来完成,请用画树状图或列表的方法,计算他们恰好选择完成同一种作品类型的概率是多少.22. 如图,四边形ABCD内接于⊙O,对角线AC,BD交于点E. (1)、求证:△AED∽△BEC;(2)、若BD平分∠ABC,求证:CD2=DE•DB;(3)、在(2)小题的条件下,若DE=4,BE=2,过圆心O点,作OF⊥CD于点F,OF=2,求该圆的半径长.23. 如图,点D在反比例函数y= (k>0,x>0)图象上,四边形ABCD是矩形,点A和点B在y轴上,连接CA,交反比例函数图象于点F,并延长交x轴于点E,连接BE.
(1)、求证:△AED∽△BEC;(2)、若BD平分∠ABC,求证:CD2=DE•DB;(3)、在(2)小题的条件下,若DE=4,BE=2,过圆心O点,作OF⊥CD于点F,OF=2,求该圆的半径长.23. 如图,点D在反比例函数y= (k>0,x>0)图象上,四边形ABCD是矩形,点A和点B在y轴上,连接CA,交反比例函数图象于点F,并延长交x轴于点E,连接BE. (1)、若D点坐标是(5,2),求反比例函数的表达式;(2)、在(1)小题的条件下,若CE所在直线的表达式是y= x+2,求F点的坐标;(3)、若△ABE的面积为4 ,求k的值.24. 某超市前期以每件40元的价格购进了一批新上市的商品.投放市场后发现:该商品销售单价定为60元/件时,每天可销售20件;近期由于疫情的影响销量有所降低,超市为了尽快销售完这批商品,决定采用降价销售策略.据统计,该商品销售单价每降低1元,每天可以多售出2件.已知超市每天销售该商品的人工费用是180元.(1)、当该商品售价为58元/件时,求超市销售该商品每天的利润是多少元?(2)、设该商品售价为x元/件,求超市销售该商品每天的利润w(元)与售价x之间的关系;(3)、当该商品售价为多少元时,超市销售该商品每天的利润最大?最大利润是多少元?25. 如图,在平面直角坐标系中,抛物线 与x轴交于 两点,与y轴交于点C.
(1)、若D点坐标是(5,2),求反比例函数的表达式;(2)、在(1)小题的条件下,若CE所在直线的表达式是y= x+2,求F点的坐标;(3)、若△ABE的面积为4 ,求k的值.24. 某超市前期以每件40元的价格购进了一批新上市的商品.投放市场后发现:该商品销售单价定为60元/件时,每天可销售20件;近期由于疫情的影响销量有所降低,超市为了尽快销售完这批商品,决定采用降价销售策略.据统计,该商品销售单价每降低1元,每天可以多售出2件.已知超市每天销售该商品的人工费用是180元.(1)、当该商品售价为58元/件时,求超市销售该商品每天的利润是多少元?(2)、设该商品售价为x元/件,求超市销售该商品每天的利润w(元)与售价x之间的关系;(3)、当该商品售价为多少元时,超市销售该商品每天的利润最大?最大利润是多少元?25. 如图,在平面直角坐标系中,抛物线 与x轴交于 两点,与y轴交于点C. (1)、求抛物线的表达式;(2)、连接 ,在x轴上求作一点D,使 有最小值,求出此时 的度数和点D的坐标;(3)、M为线段BC中点,E为抛物线上一点,将点E绕着点M旋转180°后得点N,当四边形BECN为菱形时,求N点坐标.26. 如图,在 中, ,点M为边 的中点.点Q从点A出发,沿 方向以每秒1个单位长度的速度向终点C运动,同时点P从点C出发,以每秒2个单位长度的速度先沿 方向运动到点B,再沿 方向向终点A运动,以 、 为邻边构造 ,设点2运动的时间为t秒.
(1)、求抛物线的表达式;(2)、连接 ,在x轴上求作一点D,使 有最小值,求出此时 的度数和点D的坐标;(3)、M为线段BC中点,E为抛物线上一点,将点E绕着点M旋转180°后得点N,当四边形BECN为菱形时,求N点坐标.26. 如图,在 中, ,点M为边 的中点.点Q从点A出发,沿 方向以每秒1个单位长度的速度向终点C运动,同时点P从点C出发,以每秒2个单位长度的速度先沿 方向运动到点B,再沿 方向向终点A运动,以 、 为邻边构造 ,设点2运动的时间为t秒.

 (1)、当点E落在 边上时,求t和 的面积;(2)、当点P在边 上时,设 的面积为 ,求S与t之间的函数关系式;(3)、连接 ,直接写出 将 分成的两部分图形面积相等时t的值.
(1)、当点E落在 边上时,求t和 的面积;(2)、当点P在边 上时,设 的面积为 ,求S与t之间的函数关系式;(3)、连接 ,直接写出 将 分成的两部分图形面积相等时t的值.