陕西省宝鸡市凤翔区2022年九年级第二次模拟数学试卷

试卷更新日期：2022-06-10 类型：中考模拟

进入出卷网下载

一、单选题

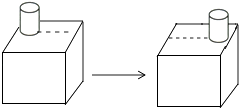
1. 徐志摩的《泰山日出》一文描写了“泰山佛光”壮丽景象.若1月份的泰山山脚平均气温为9℃，山顶平均气温为－2℃，则山脚平均气温与山顶平均气温的温差是（）

A、11℃ B、－11℃ C、7℃ D、－7℃

查看试题解析
2. 如图，一个圆柱体在正方体上沿虚线从左向右平移，平移过程中不变的是（）

A、主视图 B、左视图 C、俯视图 D、主视图和俯视图

查看试题解析
3. 宝鸡，古称陈仓、雍城，誉称“炎帝故里、青铜器之乡”，地处关中平原西部，总面积约18000平方公里，数据18000用科学记数法表示为（）

A、 $18 \times 10^{3}$ B、 $1.8 \times 10^{5}$ C、 $1.8 \times 10^{4}$ D、 $1.8 \times 10^{3}$

查看试题解析
4. 计算 ${(- 3 a^{3} b^{2})}^{3}$ 的结果是（）

A、 $- 27 a^{9} b^{6}$ B、 $27 a^{9} b^{5}$ C、 $- 27 a^{6} b^{6}$ D、 $27 a^{6} b^{5}$

查看试题解析
5. 如图，已知 $△ A B C$ 与 $△ A D E$ 中， $∠ C = ∠ A E D = 90 °$ ，点E在AB上，那么添加下列一个条件后，仍然不能判定 $△ A B C$ 与 $△ A D E$ 相似的是（）

A、 $∠ C A B = ∠ D$ B、 $\frac{A C}{B C} = \frac{D E}{A E}$ C、 $A D ∥ B C$ D、 $\frac{B C}{A C} = \frac{A D}{A E}$

查看试题解析
6. 在平面直角坐标系中，若将一次函数 $y = - 2 x + b$ 的图象关于x轴对称后经过点 $(0 ， - 2)$ ，则b的值为（）

A、－1 B、1 C、2 D、－2

查看试题解析
7. 如图，在 $⊙ O$ 中，弦 $A B = 2 \sqrt{2}$ ，点C是 $⊙ O$ 上一点，且 $∠ A C B = 45 °$ ，则劣弧 $\overset{⌢}{A B}$ 的长为（）

A、 $\frac{π}{2}$ B、 $π$ C、 $\sqrt{2} π$ D、 $2 π$

查看试题解析

8. 二次函数

y = a x^{2} + b x + c (a \neq 0)

中的自变量x与函数值y的部分对应值如下表：

x	…	－3	－2	－1	0	1	4	…
y	…	16	7	0	－5	－8	－5	…

则下列说法正确的是（）

A、

a < 0

B、顶点坐标为

(1 ， - 8)

C、该函数的图象与x轴仅有一个交点 D、若点

P (- 2.5 ， y_{1}) 、 Q (5 ， y_{2})

在该二次函数图象上，则

y_{1} > y_{2}

查看试题解析

二、填空题

9. 已知正六边形的边长为4，则它的内切圆的半径为.

查看试题解析
10. 数学是研究化学的重要工具，数学知识广泛应用于化学领域，比如在学习化学的醇类分子式中，甲醇分子式为 ${CH}_{3} OH$ ，乙醇分子式为 $C_{2} H_{5} OH$ ，丙醇分子式为 $C_{3} H_{7} OH \cdot \cdot \cdot$ ，设碳原子的数目为n（n为正整数），则醇类的分子式可以用式子来表示.

查看试题解析
11. 如图， $▱ A B C D$ 的顶点A在反比例函数 $y = \frac{k}{x}$ （ $x > 0$ ，k为常数， $k \neq 0$ ）的图象上，点B在y轴上，点C，点D在x轴上，AD与y轴交于点E，连接CE，若 $S_{△ B C E} = 4$ ，则k的值为.

查看试题解析
12. 如图，正方形ABCD的边长是4，F点是BC边的中点，点H是CD边上的一个动点，以CH为直径作 $⊙ O$ ，连接HF交 $⊙ O$ 于E点，连接DE，则线段DE的最小值为.

查看试题解析

三、解答题

13. 计算： $2 \sin 60 ° + {(- \frac{1}{2})}^{- 2} - \sqrt{12}$ .

查看试题解析
14. 解不等式 $\frac{2 x + 1}{4} \leq \frac{x - 1}{3} + 1$ ，并写出它的非负整数解

查看试题解析
15. 解方程： $\frac{2 x}{x - 1} - \frac{x - 1}{x^{2} - 1} = 2$ .

查看试题解析
16. 如图，在 $Rt △ A B C$ 中， $∠ C = 90 °$ ， $∠ B A C = 30 °$ ，请利用尺规作图法在边BC上找一点D，使得 $∠ A D B = 105 °$ .（保留作图痕迹，不写作法）

查看试题解析
17. 如图，D、E、F分别是 $△ A B C$ 各边的中点，连接DE、EF， $A B = A C$ ，求证：四边形ADEF为菱形.

查看试题解析
18. 开展农技培训，实施人才强村战略，因地制宜采用新媒体手段远程指导生产，利用广播电视、微信公众号等开展农技培训.某地区加强了培训经费的投入，2020年投入3000万元，预计2022年投入4320万元.求该地区这两年投入培训经费的年平均增长率.

查看试题解析
19. 4月21日，教育部召开新闻发布会，介绍义务教育课程方案和课程标准修订情况.新修订的义务教育课程方案和课程标准，明确了新时代人才培养要求，绘制了未来学校育人蓝图，完善了课程设置，课程结构、考试评价，课程实施等方面要求.为了深化课程改革，某校积极开展校本课程建设，成立了多个社团，要求每位学生都自主选择且只选择其中一个社团.莉莉和天天喜欢的社团均是：A.文学鉴赏、B.科学实验、C.音乐舞蹈，她们不知道如何选择，于是打算利用抓阄的方式来选择，莉莉准备了三张完全相同的纸片，纸片上分别写上A、B、C，然后将纸片折叠成外观一致的纸团，洗匀后，莉莉先从中随机摸取一个纸团，记下字母，折好后放回洗匀，天天再从中随机摸取一个纸团，记下字母，摸到的纸团上的字母就代表自己将要选择的社团.

(1)、莉莉从中随机摸到一个纸团是C（音乐舞蹈）的概率是；

(2)、请你用列表法或画树状图法求出莉莉和天天摸取的纸团中至少有一个是A的概率.

查看试题解析
20. 宝鸡国金中心是宝鸡的地标建筑.如图，某数学兴趣小组用无人机测量宝鸡国金中心AB的高度，在飞行高度为300米的无人机上的点P处测得大楼顶部B处的俯角为33°，大楼底部A处的俯角为63.3°，求宝鸡国金中心AB的高.（参考数据： $\tan 33 ° \approx 0.65$ ， $\tan 63.3 ° \approx 2.00$ ）

查看试题解析
21. 习近平总书记指出：“考古是一项重要文化事业，也是一项具有重大社会政治意义的工作.”百年考古，成就辉煌；国家使命，陕西担当.近日，全国首座考古学科专题博物馆——陕西考古博物馆于西安正式建成，开始对外试行开放.小张期待已久，提前预约门票，骑自行车去离家20千米的考古博物馆参观，其离家的距离y（千米）随骑行时间x（时）变化的图象（全程）如图所示.

(1)、小张出发0.25小时，离家的距离是千米；

(2)、求出AB所在直线的函数关系式；

(3)、出发1.5小时，小张距终点还有多少千米？

查看试题解析

22. 近年来，随着社会的发展，学校，家庭等社会问题的日益复杂化，心理健康教育已成为学校教育的一个新课题.某中学开设了“家校心理疏导”课程，为了解学生的前置情况，学生处对全校学生进行了问卷测评，从中随机抽取了50份问卷，统计成绩，并将结果绘制出不完整的频数分布表和频数分布直方图如图表：

组别	成绩x（分）	频数（人数）	合组总分（分）
第1组	$50 \leq x < 60$	4	220
第2组	$60 \leq x < 70$	8	520
第3组	$70 \leq x < 80$	16	1200
第4组	$80 \leq x < 90$	a	1020
第5组	$90 \leq x \leq 100$	10	950

根据以上信息，回答下列问题：

(1)、a= ，并补全频数分布直方图；

(2)、本次所抽取的学生测评成绩的中位数位于哪个组？并求本次所抽取的学生测评成绩的平均数；

(3)、若测评成绩不低于80分为优秀，试估计该校2000名学生测评成绩为优秀的人数是多少？

查看试题解析

23. 如图， $A B = B C$ ，以BC 为直径作 $⊙ O$ ， AC交 $⊙ O$ 于点E，过点E作 $E G ⊥ A B$ 于点F，交CB的延长线于点G．

(1)、求证：EG是 $⊙ O$ 的切线；

(2)、若 $G F = 4 \sqrt{3}$ ， $G B = 8$ ，求 $⊙ O$ 的半径．

查看试题解析
24. 如图，在平面直角坐标系中，抛物线 $C_{1} ： y = x^{2} + b x + c$ 的图象经过 $A (- 1 ， 0)$ ， $C (0 ， - 2)$ 两点，将抛物线 $C_{1}$ 向右平移2个单位得到抛物线 $C_{2}$ ，平移后点A的对应点为点B.

(1)、求抛物线 $C_{1}$ 与 $C_{2}$ 的函数表达式；

(2)、若点M是抛物线 $C_{1}$ 上一动点，点N是抛物线 $C_{2}$ 上一动点，请问是否存在这样的点M、N，使得以A、B、M、N为顶点且以AB为边的四边形是面积为8的平行四边形？若存在，求出点M、N的坐标；若不存在，请说明理由.

查看试题解析
25.

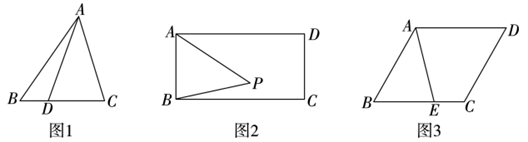(1)、问题提出如图1，在 $△ A B C$ 中，点D在BC上，连接AD， $C D = 2 B D$ ，则 $△ A B D$ 与 $△ A C D$ 的面积之比为；

(2)、问题探究
如图2，在矩形ABCD中， $A B = 4$ ， $B C = 8$ ，点P为矩形内一动点，在点P运动的过程中始终有 $∠ A P B = 45 °$ ，求 $△ A P B$ 面积的最大值；（结果保留根号）

(3)、问题解决
如图3，某市欲规划一块形如平行四边形ABCD的休闲旅游观光区，点A为观光区的人口，并满足 $∠ B A D = 120 °$ ，要求在边BC上确定一点E为观光区的南门，为了方便市民游览，修建一条观光通道AE（观光通道的宽度不计），且 $B E = 2 C E$ ， $A E = 300$ 米，为了容纳尽可能多的游客，要求平行四边形ABCD的面积最大，请问是否存在满足上述条件的面积最大的平行四边形ABCD？若存在，求出平行四边形ABCD的最大面积；若不存在，请说明理由.（结果保留根号）

查看试题解析