四川省德阳市广汉市2022年九年级第一次诊断考试数学试卷
试卷更新日期:2022-06-10 类型:中考模拟
一、单选题
-
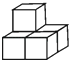
1. 3的倒数等于( )A、 3 B、 C、– 3 D、–2. 如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、4x3•2x2=8x6 B、a4+a3=a7 C、(﹣x2)5=﹣x10 D、(a﹣b)2=a2﹣b24. 如图所示的四个图案是四国冬季奥林匹克运动会会徽图案上的一部分图形,其中为轴对称图形的是( )A、
3. 下列计算正确的是( )A、4x3•2x2=8x6 B、a4+a3=a7 C、(﹣x2)5=﹣x10 D、(a﹣b)2=a2﹣b24. 如图所示的四个图案是四国冬季奥林匹克运动会会徽图案上的一部分图形,其中为轴对称图形的是( )A、 B、
B、 C、
C、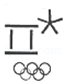 D、
D、 5. 拒绝“餐桌浪费”,刻不容缓.节约一粒米的帐:一个人一日三餐少浪费一粒米,全国一年就可以节省3240万斤,这些粮食可供9万人吃一年.“3240万”这个数据用科学记数法表示为( )A、0.324×108 B、32.4×106 C、3.24×107 D、324×1086. 某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是( )A、50(1+2x)=182 B、50+50(1+x)+50(1+2x)=182 C、50(1+x)2=182 D、50+50(1+x)+50(1+x)2=1827.
5. 拒绝“餐桌浪费”,刻不容缓.节约一粒米的帐:一个人一日三餐少浪费一粒米,全国一年就可以节省3240万斤,这些粮食可供9万人吃一年.“3240万”这个数据用科学记数法表示为( )A、0.324×108 B、32.4×106 C、3.24×107 D、324×1086. 某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是( )A、50(1+2x)=182 B、50+50(1+x)+50(1+2x)=182 C、50(1+x)2=182 D、50+50(1+x)+50(1+x)2=1827.抛物线y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y= 在同一平面直角坐标系内的图象大致为( )
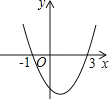 A、
A、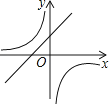 B、
B、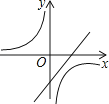 C、
C、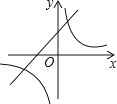 D、
D、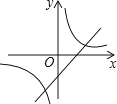 8. 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为4,则这个正六边形的边心距OM和 的长分别为( )
8. 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为4,则这个正六边形的边心距OM和 的长分别为( ) A、2, B、 , π C、2 , D、2 ,9.
A、2, B、 , π C、2 , D、2 ,9.如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为
( )
 A、2 B、3 C、4 D、510. 如图,菱形ABCD中, , ,M为AB的中点.动点P在菱形的边上从点B出发,沿 的方向运动,到达点D时停止.连接MP,设点P运动的路程为x, ,则表示y与x的函数关系的图象大致为( )
A、2 B、3 C、4 D、510. 如图,菱形ABCD中, , ,M为AB的中点.动点P在菱形的边上从点B出发,沿 的方向运动,到达点D时停止.连接MP,设点P运动的路程为x, ,则表示y与x的函数关系的图象大致为( ) A、
A、 B、
B、 C、
C、 D、
D、 11. 在Rt△ABC中,∠C=90°,AC=10,BC=12,点D为线段BC上一动点.以CD为⊙O直径,作AD交⊙O于点E,连BE,则BE的最小值为( )
11. 在Rt△ABC中,∠C=90°,AC=10,BC=12,点D为线段BC上一动点.以CD为⊙O直径,作AD交⊙O于点E,连BE,则BE的最小值为( ) A、6 B、8 C、10 D、1212. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac﹣b2>8a;④; ⑤b>c.
A、6 B、8 C、10 D、1212. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac﹣b2>8a;④; ⑤b>c.
其中含所有正确结论的选项是( )
A、①②③ B、②③④ C、①④⑤ D、①③④⑤二、填空题
-
13. 分解因式: .14. 若代数式 有意义,则m的取值范围是.15. 设 分别为一元二次方程 的两个实数根,则 .16. 如图,已知⊙ 是 的内切圆,且 , ,则 的度数为 .
 17. 如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,过E点作EH⊥CD于H,则EH的长为.
17. 如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,过E点作EH⊥CD于H,则EH的长为. 18. 点A、C为半径是8的圆周上两动点,点B为 的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆半径的中点上,则该菱形的边长为.
18. 点A、C为半径是8的圆周上两动点,点B为 的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆半径的中点上,则该菱形的边长为.
三、解答题
-
19. 计算:20. 如图,平行四边形ABCD的对角线AC、BD相交于点O,AF=CE.
 (1)、求证:△BAE≌△DCF;(2)、若BD⊥EF,连接DE、BF,判断四边形EBFD的形状,并说明理由.21. 济南某中学在参加“创文明城,点赞泉城”书画比赛中,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作鼎的数量进行了分析统计,制作了两幅不完整的统计图.
(1)、求证:△BAE≌△DCF;(2)、若BD⊥EF,连接DE、BF,判断四边形EBFD的形状,并说明理由.21. 济南某中学在参加“创文明城,点赞泉城”书画比赛中,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作鼎的数量进行了分析统计,制作了两幅不完整的统计图.
请根据以上信息,回答下列问题:
(1)、杨老师采用的调查方式是(填“普查”或“抽样调查”);(2)、请补充完整条形统计图,并计算扇形统计图中C班作品数量所对应的圆心角度数.(3)、请估计全校共征集作品的件数.(4)、如果全枝征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一样等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.22. 如图,在平面直角坐标系中,直线l1:y=﹣ x与反比例函数y= 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;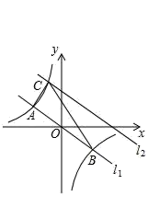 (1)、求反比例函数的表达式;(2)、根据图象直接写出﹣ x> 的解集;(3)、将直线l1:y=﹣ x沿y向上平移后的直线l2与反比例函数y= 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.23. 某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他费用80元.
(1)、求反比例函数的表达式;(2)、根据图象直接写出﹣ x> 的解集;(3)、将直线l1:y=﹣ x沿y向上平移后的直线l2与反比例函数y= 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.23. 某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他费用80元.销售单价 (元)
3.5
5.5
销售量 (袋)
280
120
(1)、请直接写出y与x之间的函数关系式;(2)、如果每天获得160元的利润,销售单价为多少元?(3)、设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?24. 如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P. (1)、求证:PD是⊙O的切线;(2)、求证:△PBD∽△DCA;(3)、当AB=6,AC=8时,求线段PB的长.25. 如图①已知抛物线y=ax2﹣3ax﹣4a(a<0)的图象与x轴交于A、B两点(A在B的左侧),与y的正半轴交于点C,连结BC,二次函数的对称轴与x轴的交点为E.
(1)、求证:PD是⊙O的切线;(2)、求证:△PBD∽△DCA;(3)、当AB=6,AC=8时,求线段PB的长.25. 如图①已知抛物线y=ax2﹣3ax﹣4a(a<0)的图象与x轴交于A、B两点(A在B的左侧),与y的正半轴交于点C,连结BC,二次函数的对称轴与x轴的交点为E. (1)、抛物线的对称轴与x轴的交点E坐标为 , 点A的坐标为;
(1)、抛物线的对称轴与x轴的交点E坐标为 , 点A的坐标为;的坐标;若不存在,请说明理由.
(2)、若以E为圆心的圆与y轴和直线BC都相切,试求出抛物线的解析式;(3)、在(2)的条件下,如图②Q(m,0)是x的正半轴上一点,过点Q作y轴的平行线,与直线BC交于点M,与抛物线交于点N,连结CN,将△CMN沿CN翻折,M的对应点为M′.在图②中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q