四川省德阳广汉市2022年九年级第二次诊断考试数学试卷

试卷更新日期：2022-06-10 类型：中考模拟

进入出卷网下载

一、单选题

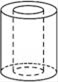
1. 给出四个数－1，0， 0.5， $\sqrt{7}$ ，其中为无理数的是（）

A、－1. B、0 C、0.5 D、 $\sqrt{7}$

查看试题解析
2. 如图是一个空心圆柱体，其俯视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{{(- 4)}^{2}}$ =-4 B、（a²）³=a⁵ C、2a-a=2 D、a•a³=a⁴

查看试题解析
4. 如图，这是根据某班40名同学一周的体育锻炼情况绘制的条形统计图，根据统计图提供的信息，可得到该班40名同学一周参加体育锻炼时间的众数、中位数分别是（）

A、8，9 B、8，8.5 C、16，8.5 D、16，10.5

查看试题解析
5. 在平面直角坐标系中，如果抛物线 $y = 2 x^{2}$ 不动，而把x轴、y轴分别向上、向右平移2个单位，那么在新坐标系下抛物线的解析式是（）

A、 $y = 2 {(x - 2)}^{2} + 2$ B、 $y = 2 {(x - 2)}^{2} - 2$ C、 $y = 2 {(x + 2)}^{2} - 2$ D、 $y = 2 {(x + 2)}^{2} + 2$

查看试题解析
6. “五一”节期间，几名同学包租一辆面包车前去旅游，面包车的租价为180元，出发时又增加了两名同学，结果每个同学比原来少摊了3元钱车费，设实际参加游览的同学共x人，则所列方程为（）

A、 $\frac{180}{x} - \frac{180}{x + 2} = 3$ B、 $\frac{180}{x + 2} - \frac{180}{x} = 3$ C、 $\frac{180}{x} - \frac{180}{x - 2} = 3$ D、 $\frac{180}{x - 2} - \frac{180}{x} = 3$

查看试题解析
7. 如图，在 $△ A B C$ 中，点D，E分别为AB，AC边上的点，且 $D E / / B C$ ，CD、BE相较于点O，连接AO并延长交DE于点G，交BC边于点F，则下列结论中一定正确的是 $($ 　　 $)$

A、 $\frac{A D}{A B} = \frac{A E}{E C}$ B、 $\frac{A G}{G F} = \frac{A E}{B D}$ C、 $\frac{O D}{O C} = \frac{A E}{A C}$ D、 $\frac{A G}{A F} = \frac{A C}{E C}$

查看试题解析
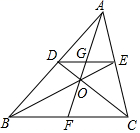8. 如图，已知⊙O的半径是2，点A，B，C在⊙O上，若四边形OABC为菱形，则图中阴影部分面积为（）

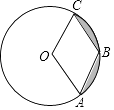A、 $\frac{2}{3}$ π﹣2 $\sqrt{3}$ B、 $\frac{1}{3}$ π﹣ $\sqrt{3}$ C、 $\frac{4}{3}$ π﹣2 $\sqrt{3}$ D、 $\frac{4}{3}$ π﹣ $\sqrt{3}$

查看试题解析
9. 如图，在矩形ABCD中，AB＝8，BC＝12，点E是BC的中点，连接AE，将△ABE沿AE折叠，点B落在点F处，连接FC，则sin∠ECF＝（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
10. 若数a使得关于x的分式方程 $\frac{a}{x - 1} - \frac{x - 3}{1 - x} = 5$ 有正数解，且使得关于y的不等式组 ${\begin{array}{l} 2 y - a \geq y - 1 \\ \frac{1}{2} y + a < 3 \end{array}$ 有解，那么符合条件的所有整数a的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
11. 如图，在正方形ABCD和正方形DEFG中，点G在CD上，DE=2，将正方形DEFG绕点D顺时针旋转60°，得到正方形DE′F′G′，此时点G′在AC上，连接CE′，则CE′+CG′=（）

A、 $\sqrt{2} + \sqrt{6}$ B、 $\sqrt{3} + 1$ C、 $\sqrt{3} + \sqrt{2}$ D、 $\sqrt{3} + \sqrt{6}$

查看试题解析
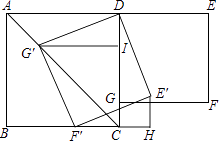12. 如图，抛物线 $y = a x^{2} + b x + c$ 与 $x$ 轴交于点A（-1，0），顶点坐标（1，n）与 $y$ 轴的交点在（0，2），（0，3）之间（包含端点），则下列结论：① $3 a + b < 0$ ；② $- 1 \leq a \leq - \frac{2}{3}$ ；③对于任意实数m，a+b≥am²+bm总成立；④关于 $x$ 的方程 $a x^{2} + b x + c = n - 1$ 有两个不相等的实数根.其中结论正确的个数为 $($ 　　 $)$

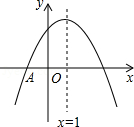A、1 个 B、2 个 C、3 个 D、4 个

查看试题解析

二、填空题

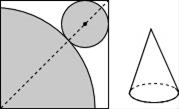
13. 如果5x+3与﹣2x+9是互为相反数，则x﹣2的值是.

查看试题解析
14. 新型冠状病毒是一种形状为冠状的病毒，其直径大约为 $0.000000102 m$ ，将 $0.000000102$ 用科学记数法表示为．

查看试题解析
15. 在纸上剪下一个圆和一个扇形纸片，使它们恰好围成一个圆锥（如图所示），如果扇形的圆心角为90°，扇形的半径为4，那么所围成的圆锥的高为.

查看试题解析
16. 若函数y= ${\begin{array}{l} x^{2} + 2 (x \leq 2) \\ 2 x (x > 2) \end{array}$ ，则当函数值y＝8时，自变量x的值等于.

查看试题解析
17. 如图，点A，B为反比例函数 $y = \frac{k}{x}$ 在第一象限上的两点， $A C ⊥ y$ 轴于点C， $B D ⊥ x$ 轴于点D，若B点的横坐标是A点横坐标的一半，且图中阴影部分的面积为 $k - 2$ ，则k的值为.

查看试题解析
18. 如图，在△ABC中，4AB=5AC，AD为△ABC的角平分线，点E在BC的延长线上，EF⊥AD于点F，点G在AF上，FG=FD，连接EG交AC于点H.若点H是AC的中点，则 $\frac{A G}{F D}$ 的值为.

查看试题解析

三、解答题

19. 计算：|− $\sqrt{3}$ |-（-4）^-1+( $\frac{π}{\sqrt{3} - 2}$ )⁰-2cos30°

查看试题解析
20. 已知，如图，菱形ABCD中，E、F分别是CD、CB上的点，且CE＝CF；

(1)、求证：△ABE≌△ADF

(2)、若菱形ABCD中，AB＝4，∠C＝120°，∠EAF＝60°，求菱形ABCD的面积.

查看试题解析
21. 某校开展了以“责任、感恩”为主题的班队活动，活动结束后，初三（2）班数学兴趣小组提出了5个主要观点并在本班学生中进行了调查（要求每位同学只选自己最认可的一项观点），并制成了如下扇形统计图，

(1)、该班有人，学生选择“和谐”观点的有人，在扇形统计图中，“和谐”观点所在扇形区域的圆心角是度；

(2)、如果该校有360名初三学生，利用样本估计选择“感恩”观点的初三学生约有人；

(3)、如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查，求恰好选到“和谐”和“感恩”观点的概率（用树状图或列表法分析解答）.

查看试题解析
22. 如图，在平面直角坐标系xOy中，已知正比例函数y₁＝﹣2x的图象与反比例函数y₂＝ $\frac{k}{x}$ 的图象交于A（﹣1，n），B两点.

(1)、求出反比例函数的解析式及点B的坐标；

(2)、观察图象，请直接写出满足 y₂ ≤2的取值范围

(3)、点P是第四象限内反比例函数的图象上一点，若△POB的面积为1，请直接写出点P的横坐标.

查看试题解析
23. 某企业信息部进行市场调研发现：信息一：如果单独投资A种产品，所获利润y_A(万元)与投资金额x(万元)之间存在某种关系的部分对应值如下表：
x(万元)
1
2
2.5
3
5
y_A(万元)
0.4
0.8
1
1.2
2
信息二：如果单独投资B种产品，则所获利润y_B(万元)与投资金额x(万元)之间存在二次函数关系：y_B＝ax²+bx，且投资2万元时获利润2.4万元，当投资4万元时，可获利润3.2万元．

(1)、求出y_B与x的函数关系式．

(2)、从所学过的一次函数、二次函数、反比例函数中确定哪种函数能表示y_A与x之间的关系，并求出y_A与x的函数关系式．

(3)、如果企业同时对A、B两种产品共投资15万元，请设计一个能获得最大利润的投资方案，并求出按此方案能获得的最大利润是多少？

查看试题解析
24. 如图，在Rt△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，O为AB上一点，经过点A，D的⊙O分别交AB，AC于点E，F，连接OF交AD于点G．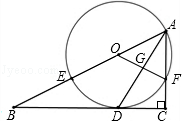

(1)、求证：BC是⊙O的切线；

(2)、设AB＝x，AF＝y，试用含x，y的代数式表示线段AD的长；

(3)、若BE＝8，sinB＝ $\frac{5}{13}$ ，求DG的长，

查看试题解析
25. 如图，已知抛物线y＝﹣x²+bx+c与一直线相交于A（1，0）、C（﹣2，3）两点，与y轴交于点N，其顶点为D．

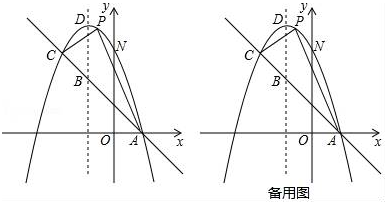(1)、求抛物线及直线AC的函数关系式；

(2)、若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值及此时点P的坐标；

(3)、在对称轴上是否存在一点M，使△ANM的周长最小．若存在，请求出M点的坐标和△ANM周长的最小值；若不存在，请说明理由．

查看试题解析

x(万元)	1	2	2.5	3	5
y_A(万元)	0.4	0.8	1	1.2	2