四川省成都市温江区2022年九年级数学适应性考试数学试卷
试卷更新日期:2022-06-10 类型:中考模拟
一、单选题
-
1. 由5个相同的小立方体搭成的几何体如图所示,则它的俯视图为( )
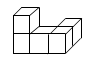 A、
A、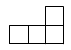 B、
B、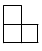 C、
C、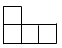 D、
D、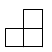 2. 根据世卫组织统计数据,截至2022年4月26日,全球累计新冠肺炎确诊病例5.09亿例,将数据5.09亿用科学记数法表示为( )A、 B、 C、 D、3. 在平面直角坐标系中,将点A(-2,3)向左平移3个单位长度后得到的点的坐标为( )A、(-5,3) B、(1,3) C、(-2,0) D、(-2,6)4. 如图,将一块含有45°角的直角三角板放置在两条平行线上,若∠1=25°,则∠2为( )
2. 根据世卫组织统计数据,截至2022年4月26日,全球累计新冠肺炎确诊病例5.09亿例,将数据5.09亿用科学记数法表示为( )A、 B、 C、 D、3. 在平面直角坐标系中,将点A(-2,3)向左平移3个单位长度后得到的点的坐标为( )A、(-5,3) B、(1,3) C、(-2,0) D、(-2,6)4. 如图,将一块含有45°角的直角三角板放置在两条平行线上,若∠1=25°,则∠2为( ) A、15° B、20° C、25° D、30°5. 下列计算正确的是( )A、 B、 C、 D、6. 冬季奥林匹克运动会(Olympic Winter Games),简称为冬季奥运会、冬奥会,是世界规模最大的冬季综合性运动会,每四年举办一届,最近四届中国获得奖牌总数分别为11,9,9,15,则这组数据的中位数是( )A、9 B、10 C、11 D、127. 分式方程的解是( )A、 B、 C、 D、8. 如图,二次函数的图象过点(1,0),对称轴为直线 , 则下列结论中不正确的是( )
A、15° B、20° C、25° D、30°5. 下列计算正确的是( )A、 B、 C、 D、6. 冬季奥林匹克运动会(Olympic Winter Games),简称为冬季奥运会、冬奥会,是世界规模最大的冬季综合性运动会,每四年举办一届,最近四届中国获得奖牌总数分别为11,9,9,15,则这组数据的中位数是( )A、9 B、10 C、11 D、127. 分式方程的解是( )A、 B、 C、 D、8. 如图,二次函数的图象过点(1,0),对称轴为直线 , 则下列结论中不正确的是( ) A、 B、 C、函数的最小值为 D、
A、 B、 C、函数的最小值为 D、二、填空题
-
9. 若m-1与-3互为相反数,则m的值为.10. 分解因式: .11. 一次函数的值随着x值的增大而减小,则常数m的取值范围为.12. 如图,C,D是⊙O上直径AB两侧的两点,设 , 则.
 13. 如图,在中, , 按以下步骤作图:①以B为圆心,以任意长为半径作弧,分别交AB,BC于点M,N;②分别以M、N为圆心,以大于的长为半径作弧,两弧在内交于点P;③作射线BP,交AC于点D.若 , , 则线段AD的长为.
13. 如图,在中, , 按以下步骤作图:①以B为圆心,以任意长为半径作弧,分别交AB,BC于点M,N;②分别以M、N为圆心,以大于的长为半径作弧,两弧在内交于点P;③作射线BP,交AC于点D.若 , , 则线段AD的长为. 14. 化简:.15. 已知关于x的一元二次方程有两个实数根分别为 , .若 , 则m的值为.16. 从-1,1,2中任取一个数作为k,从-1,0,1,2中任取一个数作为b,则一次函数的图象不经过第三象限的概率是.17. 如图,在正方形ABCD中, , E为BC中点,沿直线DF翻折 , 使点A的对应点A′恰好落在线段AE上,分别在AD,上取点M,N,沿直线MN继续翻折,使点与点D重合,则线段MN的长为.
14. 化简:.15. 已知关于x的一元二次方程有两个实数根分别为 , .若 , 则m的值为.16. 从-1,1,2中任取一个数作为k,从-1,0,1,2中任取一个数作为b,则一次函数的图象不经过第三象限的概率是.17. 如图,在正方形ABCD中, , E为BC中点,沿直线DF翻折 , 使点A的对应点A′恰好落在线段AE上,分别在AD,上取点M,N,沿直线MN继续翻折,使点与点D重合,则线段MN的长为. 18. 在中,斜边 , , 点D是AC边上的一个动点,连接BD,将线段BD绕点B顺时针旋转60°得到BE,连接CE,则BE+CE的最小值为.
18. 在中,斜边 , , 点D是AC边上的一个动点,连接BD,将线段BD绕点B顺时针旋转60°得到BE,连接CE,则BE+CE的最小值为.
三、解答题
-
19.(1)、计算:.(2)、解不等式组:20. 为庆祝中国共产主义青年团成立100周年,某校举行共青团团史知识竞赛活动.赛后随机抽取了部分学生的成绩,按得分划分为A,B,C,D四个等级,并绘制了如下不完整的统计表和统计图.
等级
成绩(x)
人数
A
80≤x≤100
m
B
70≤x<80
15
C
60≤x<70
n
D
X<60
4

根据图表信息,回答下列问题:
(1)、分别求出表中m,n的值;(2)、求扇形统计图中,D等级对应的扇形圆心角度数;若全校共有1800名学生参加了此次知识竞赛活动,请估计该校成绩为A等级的学生人数.(3)、学校拟在成绩为100分的甲、乙、丙、丁四名学生中,随机抽取两名学生参加市级比赛,请用树状图或列表法表示所有可能的结果,并求甲、乙两名学生中恰好只有1人被选中的概率.21. 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高是46m,求河流的宽度BC.(结果精确到1m;参考数据: , , , ) 22. 如图,AB为⊙O的直径,C、E为圆上的两点,连接AC,BC,CE为∠AEO的角平分线,AE⊥CD,垂足为F
22. 如图,AB为⊙O的直径,C、E为圆上的两点,连接AC,BC,CE为∠AEO的角平分线,AE⊥CD,垂足为F (1)、求证:CD是⊙O的切线;(2)、若 , ⊙O的半径为6,求DF的长.23. 在平面直角坐标系xOy中,一次函数的图象由正比例函数的图象向下平移3个单位长度得到,一次函数与反比例函数的图象交于A,B两点,与x轴、y轴分别交于点C,D,且
(1)、求证:CD是⊙O的切线;(2)、若 , ⊙O的半径为6,求DF的长.23. 在平面直角坐标系xOy中,一次函数的图象由正比例函数的图象向下平移3个单位长度得到,一次函数与反比例函数的图象交于A,B两点,与x轴、y轴分别交于点C,D,且 (1)、求一次函数和反比例函数的表达式;(2)、点E在x轴上,连接AE,DE, , 直线AE与反比例函数的图象交于另一点F,求的面积.24. 四川花木看成都,成都花木看温江,温江花木看寿安,“寿安花木编艺”已被列入成都市非物质文化遗产保护名录.寿安镇以“乡村振兴”为目标,通过花木编艺的发展带动社区经济的发展.该镇花木编艺师小李,制作2个“动物”造型编艺品和3个“花瓶”造型编艺品需要成本580元,制作3个“动物”造型编艺品和7个“花瓶”造型编艺品需要成本1120元.小李通过西部花木交易中心销售编艺品并能全部售出,每个“动物”造型编艺品售价500元,每个“花瓶”造型编艺品售价300元.小李每天可以制作1个“动物”造型编艺品或者1.5个“花瓶”造型编艺品,且每月制作的“花瓶”造型编艺品不小于“动物”造型编艺品的2倍(注:每月制作的“动物”造型编艺品、“花瓶”造型编艺品的个数均为整数).假设小李每月有22天制作编艺品,其中制作“动物”造型编艺品x天,制作两类编艺品的月利润为y元.(1)、求小李制作一个“动物”造型编艺品和一个“花瓶”造型编艺品的成本分别是多少元?(2)、求y与x之间的函数关系式,并写出x的范围;(3)、小李每月制作“动物”造型编艺品多少个时,月利润y最大,最大利润是多少元?25. 在平面直角坐标系xOy中,已知抛物线与x轴交于A(1,0),B(3,0),与y轴交于点C(0,-3).
(1)、求一次函数和反比例函数的表达式;(2)、点E在x轴上,连接AE,DE, , 直线AE与反比例函数的图象交于另一点F,求的面积.24. 四川花木看成都,成都花木看温江,温江花木看寿安,“寿安花木编艺”已被列入成都市非物质文化遗产保护名录.寿安镇以“乡村振兴”为目标,通过花木编艺的发展带动社区经济的发展.该镇花木编艺师小李,制作2个“动物”造型编艺品和3个“花瓶”造型编艺品需要成本580元,制作3个“动物”造型编艺品和7个“花瓶”造型编艺品需要成本1120元.小李通过西部花木交易中心销售编艺品并能全部售出,每个“动物”造型编艺品售价500元,每个“花瓶”造型编艺品售价300元.小李每天可以制作1个“动物”造型编艺品或者1.5个“花瓶”造型编艺品,且每月制作的“花瓶”造型编艺品不小于“动物”造型编艺品的2倍(注:每月制作的“动物”造型编艺品、“花瓶”造型编艺品的个数均为整数).假设小李每月有22天制作编艺品,其中制作“动物”造型编艺品x天,制作两类编艺品的月利润为y元.(1)、求小李制作一个“动物”造型编艺品和一个“花瓶”造型编艺品的成本分别是多少元?(2)、求y与x之间的函数关系式,并写出x的范围;(3)、小李每月制作“动物”造型编艺品多少个时,月利润y最大,最大利润是多少元?25. 在平面直角坐标系xOy中,已知抛物线与x轴交于A(1,0),B(3,0),与y轴交于点C(0,-3). (1)、求抛物线的函数表达式;(2)、点D为抛物线上一点,过点D作x轴的垂线,垂足为E,若 , 求点D的坐标;(3)、点P为抛物线上一点,若 , 求点P的坐标.26. 在中, , 点D为BC边上一动点(不与点B、C重合),连接AD,若 , 将线段AD绕点A逆时针旋转α,得到线段AE,连接CE和DE,AC与DE交于点F.
(1)、求抛物线的函数表达式;(2)、点D为抛物线上一点,过点D作x轴的垂线,垂足为E,若 , 求点D的坐标;(3)、点P为抛物线上一点,若 , 求点P的坐标.26. 在中, , 点D为BC边上一动点(不与点B、C重合),连接AD,若 , 将线段AD绕点A逆时针旋转α,得到线段AE,连接CE和DE,AC与DE交于点F. (1)、求证:∽;(2)、若 , 点D在BC边上运动的过程中,求的最小值.(3)、试探究AC、CD、CE之间满足的数量关系(用含α的式子表示),并证明.
(1)、求证:∽;(2)、若 , 点D在BC边上运动的过程中,求的最小值.(3)、试探究AC、CD、CE之间满足的数量关系(用含α的式子表示),并证明.