四川省成都市高新区2022年中考数学二诊试卷

试卷更新日期：2022-06-10 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣2022的倒数是（　　）

A、﹣ $\frac{1}{2022}$ B、 $\frac{1}{2022}$ C、﹣2022 D、2022

查看试题解析
2. 图是由三个相同的小正方体组成的几何体，则该几何体的主视图是（　　）

A、 B、 C、 D、

查看试题解析
3. 2022年，北京冬奥会成功举办，国家体育总局曾委托国家统计局开展的“带动三亿人参与冰雪运动”统计调查.调查数据显示，截至2021年10月，全国冰雪运动参与人数达到3.46亿人（　　）

A、34.6×10⁷ B、3.46×10⁸ C、0.346×10⁹ D、3.46×10⁹

查看试题解析
4. 如图，直线a，b被直线c所截，∠1＝50°，则∠2的度数是（　　）

A、110° B、120° C、130° D、140°

查看试题解析
5. 经过某路口的行人，可能直行，也可能左拐或右拐.假设这三种可能性相同，有两人经过该路口，则恰好两人都直行的概率是（　　）

A、 $\frac{1}{9}$ B、 $\frac{2}{9}$ C、 $\frac{1}{3}$ D、 $\frac{4}{9}$

查看试题解析
6. 《九章算术》中记录了一个问题：“以绳测井，若将绳三折测之，绳多四尺，绳多一尺，问绳长井深各几何？”其题意是：用绳子测量水井深度，那么每等份绳长比水井深度多四尺；如果将绳子折成四等份，那么每等份绳长比水井深度多一尺.问绳长和井深各多少尺？若设绳长为x尺，则下列符合题意的方程是（　　）

A、 $\frac{1}{3}$ x﹣4＝ $\frac{1}{4}$ x﹣1 B、3（x+4）＝4（x+1） C、 $\frac{1}{3}$ x+4＝ $\frac{1}{4}$ x+1 D、3x+4＝4x+1

查看试题解析
7. 关于二次函数y＝（x﹣2）²+1，下列说法中错误的是（　　）

A、图象的开口向上 B、图象的对称轴为x＝2 C、图象与y轴交于点（0，1） D、图象可以由y＝x²的图象向右平移2个单位长度，再向上平移1个单位长度得到

查看试题解析
8. 如图，在直径为AB的⊙O中，点C，D在圆上，AC=CD，若∠CAD=28°，则∠DAB的度数为（　　）

A、28° B、34° C、56° D、62°

查看试题解析

二、填空题

9. 已知a﹣2b＝3，则代数式2a﹣4b+1的值为 .

查看试题解析
10. 如图，已知△ABC≌△DBE，∠A＝36°，∠B＝40°，则∠AED的度数为 .

查看试题解析
11. 若一次函数y＝（2m﹣1）x+2的值随x值的增大而减小，则m的取值范围是 .

查看试题解析
12. 已知关于x的方程x²+3x+m＝0的一个根是1，则此方程的另一个根为 .

查看试题解析
13. 如图，在矩形ABCD中，∠ABC的平分线交AD于点E，AE＝4，DE=3，则CE＝.

查看试题解析
14. 已知a^m＝2，aⁿ＝3，则a^m+n的值为 .

查看试题解析
15. 已知关于x，y的方程组 ${\begin{array}{l} x + y = 4 k + 3 \\ x - 2 y = k \end{array}$ 的解满足x﹣y＝3，则k的值为.

查看试题解析
16. 巧板是我国古代劳动人民的一项发明，被誉为“东方魔板”，它由五块等腰直角三角形、一块正方形和一块平行四边形组成.如图是利用七巧板拼成的正方形，随机向该图形内抛一枚小针，则针尖落在阴影部分的概率为 .

查看试题解析
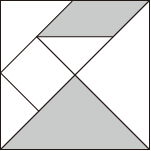17. 如图，在△ABC中，AC＝BC＝2，∠ACB=90°，点D在线段BC上，以AD为斜边作等腰直角三角形ADE，线段DE与线段AC交于点F，连接CE，若△CEF与△ABD相似，则BD的长为.

查看试题解析
18. 在平面直角坐标系中，我们把横、纵坐标都是整数的点叫做整点.如图，若“心形”图形的顶点A，B，C，D，E，F，G均为整点，已知点P（3，4），线段PQ的长为 $\sqrt{10}$ ， PQ关于过点M（0，5）的直线l对称得到P'Q'，点P的对应点为P′，当点P′恰好落在“心形”图形边的整点上时，点Q'也落在“心形”图形边的整点上，则这样的点Q′共有个.

查看试题解析

三、解答题

19.

(1)、计算：cos30°﹣| $\sqrt{3}$ ﹣2|+（ $\frac{1}{3}$ ）^﹣¹﹣（3﹣π）⁰；

(2)、化简： $\frac{2 x - 4}{x^{2} - 4} \div (1 - \frac{2}{x + 2})$ .

查看试题解析

20. 睡眠是人的机体复原整合和巩固记忆的重要环节，对促进中小学生大脑发育、骨骼生长、视力保护、身心健康和提高学习能力与效率至关重要.某校为了解本校学生的睡眠情况，随机调查了40名学生一周（7天）平购每天的睡眠时间x（单位：小时），并根据调查结果绘制成不完整的频数分布表和扇形统计图.

组别	A组	B组	C组	D组
平均每天睡眠时间	x＜8	8≤x＜9	9≤x＜10	x≥10

平均每天睡眠情况频数分布表

组别	频数
A组	4
B组	m
C组	20
D组	n

(1)、分别求出表中m，n的值；

(2)、抽取的40名学生睡眠时间的中位数落在的组别是组；

(3)、若该校共有1200名学生，请估计该校学生睡眠时间达到9小时的学生人数.

查看试题解析

21. 某商场准备改善原有自动楼梯的安全性能，把倾斜角由原来的37°减至30°（如图所示），已知原楼梯AB的长为7.5米，求BD的长.（结果精确到0.1米；参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75， $\sqrt{3}$ ≈1.73）

查看试题解析
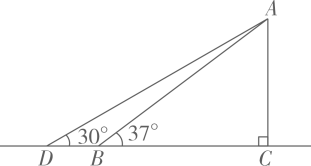22. 如图，AB为⊙O的直径，C为⊙O上一点，CD垂直AB，垂足为D，在AC延长线上取点E，使∠CBE=∠BAC.

(1)、求证：BE是⊙O的切线；

(2)、若CD＝4，BE＝6，求⊙O的半径OA.

查看试题解析
23. 在平面直角坐标系xOy中，直线y＝﹣ $\frac{1}{2}$ x+b与反比例函数y＝ $\frac{6}{x}$ 的图象交于A（2，m），B两点.

(1)、求直线AB的函数表达式；

(2)、如图1，过点A的直线分别与x轴，y轴交于点M，N，若AM=MN，连接BM，求△ABM的面积；

(3)、如图2，以AB为边作平行四边形ABCD，点C在y轴负半轴上，点D在反比例函数y＝ $\frac{k}{x}$ （k＜0）的图象上，线段AD与反比例函数y＝ $\frac{k}{x}$ （k＜0）的图象交于点E，若 $\frac{D E}{A E}$ ＝ $\frac{1}{2}$ ，求k的值.

查看试题解析
24. 为进一步丰富义务教育阶段学生假期生活，有效缓解义务教育阶段学生假期“看护难”问题，某校在寒假期间开设了丰富多彩的寒假托管服务，B两种文具奖励在此次托管服务中表现优秀的学生.已知A文具比B文具每件多5元，用900元购买B文具的数量是用600元购买A文具数量的2倍.

(1)、求A，B文具的单价；

(2)、为了调动学生的积极性，学校再次在该店购买了A，B两种文具.在购买当日，所有商品八折销售.在不超过预算资金1200元的情况下，A，B两种文具共买了90件

查看试题解析
25. 在平面直角坐标系xOy中，抛物线y＝﹣x²+bx+c与x轴分别交于点A，点B（3，0），与y轴交于点C（0，3）.

(1)、求抛物线的解析式；

(2)、如图1，连接BC，点D是直线BC上方抛物线上一动点，连接AD交BC于点E，若AE＝2ED，求点D的坐标；

(3)、直线y＝kx﹣2k+1与抛物线交于M，N两点，取点P（2，0），连接PM，PN，求△PMN面积的最小值.

查看试题解析
26. 在△ABC中，AC＝BC＝5，tanA＝ $\frac{3}{4}$ ， E分别是AB，AC边上的动点，作△ADE关于DE对称的图形△A′DE.

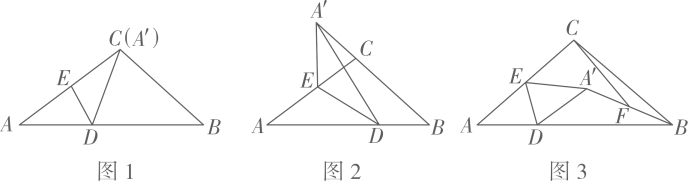(1)、如图1，当点A′恰好与点C重合，求DE的长；

(2)、如图2，当点A’落在BC的延长线上，且A’E⊥AB，求AD的长；

(3)、如图3，若AE=CE，连接A’B，F是A’B的中点，连接CF，在D点的运动过程中，求线段CF长度的最大值.

查看试题解析