四川省成都市2022年中考数学预测卷
试卷更新日期:2022-06-10 类型:中考模拟
一、单选题
-
1. 一5的绝对值是( )A、5 B、 C、 D、-52. 如图所示的几何体是由6个大小相同的小立方块搭成,其俯视图是( )
 A、
A、 B、
B、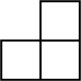 C、
C、 D、
D、 3. 在“十四五”规划的开局之年,成都一如既往是全省的“领头羊”,上半年地区生产总值为9602.72亿元.将数据“9602.72亿”用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 已知点与点关于原点成中心对称,则的值是( )A、5 B、1 C、 D、116. 国务院新闻办公室于2021年5月11日上午10时举行新闻发布会,介绍第七次全国人口普查主要数据结果,与2010年第六次全国人口普查相比,31个省份中,有25个省份人口增加.人口增长较多的5个省份依次为:广东、浙江、江苏、山东、河南,分别增加21709378人、10140697人、6088113人、5734388人、5341952人.这五个数据中,中位数是( )A、5341952 B、5734 388 C、10140697 D、60881137. 分式方程的解为( )A、 B、 C、 D、8. 如图,PA、PB是⊙O的切线,切点分别为A、B , 若OA=2,∠P=60°,则 的长为( )
3. 在“十四五”规划的开局之年,成都一如既往是全省的“领头羊”,上半年地区生产总值为9602.72亿元.将数据“9602.72亿”用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 已知点与点关于原点成中心对称,则的值是( )A、5 B、1 C、 D、116. 国务院新闻办公室于2021年5月11日上午10时举行新闻发布会,介绍第七次全国人口普查主要数据结果,与2010年第六次全国人口普查相比,31个省份中,有25个省份人口增加.人口增长较多的5个省份依次为:广东、浙江、江苏、山东、河南,分别增加21709378人、10140697人、6088113人、5734388人、5341952人.这五个数据中,中位数是( )A、5341952 B、5734 388 C、10140697 D、60881137. 分式方程的解为( )A、 B、 C、 D、8. 如图,PA、PB是⊙O的切线,切点分别为A、B , 若OA=2,∠P=60°,则 的长为( ) A、 π B、π C、 D、
A、 π B、π C、 D、二、填空题
-
9. 在等腰三角形中,已知顶角与底角的度数比为1∶2,则顶角的度数是.10. 如图,以点O为位似中心,将ΔOAB放大后得到ΔOCD,若OA=2, , 则AC=.
 11. 一次函数y=(3﹣k)x+1的图象与x轴的交点在正半轴上,则k的取值范围 .12. 当时,的值为.13. 如图,已知为的直径,C为圆上(除A,B外)一动点,按以下步骤作图:①以C为圆心,任意长为半径作弧,分别交 , 于点M,N;②分别以M,N为圆心,以大于的长为半径作弧,两弧相交于点P;作射线 , 交于点Q;③连接.若 , 则的长为.
11. 一次函数y=(3﹣k)x+1的图象与x轴的交点在正半轴上,则k的取值范围 .12. 当时,的值为.13. 如图,已知为的直径,C为圆上(除A,B外)一动点,按以下步骤作图:①以C为圆心,任意长为半径作弧,分别交 , 于点M,N;②分别以M,N为圆心,以大于的长为半径作弧,两弧相交于点P;作射线 , 交于点Q;③连接.若 , 则的长为. 14. 已知x,y均为实数, , 则的值为.15. 已知是方程的两个实数根,则的值为.16. 如图,已知的两条直径 , 互相垂直,和所对的圆心角都为 , 且.现随机地向该图形内掷一枚小针,记针尖落在和所围封闭区域内的概率为 , 针尖落在内的概率为 , 则.
14. 已知x,y均为实数, , 则的值为.15. 已知是方程的两个实数根,则的值为.16. 如图,已知的两条直径 , 互相垂直,和所对的圆心角都为 , 且.现随机地向该图形内掷一枚小针,记针尖落在和所围封闭区域内的概率为 , 针尖落在内的概率为 , 则. 17. 如图,在等腰中,已知 , , 且边在直线a上.将绕点A顺时针旋转到位置①可得到点 , 此时;将位置①的三角形绕点顺时针旋转到位置②,可得到点 , 此时;将位置②的三角形绕点顺时针旋转到位置③,可得到点 , 此时;···,按此规律继续旋转,直至得到点为止,则.
17. 如图,在等腰中,已知 , , 且边在直线a上.将绕点A顺时针旋转到位置①可得到点 , 此时;将位置①的三角形绕点顺时针旋转到位置②,可得到点 , 此时;将位置②的三角形绕点顺时针旋转到位置③,可得到点 , 此时;···,按此规律继续旋转,直至得到点为止,则.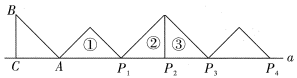 18. 如图,和是两个具有公共边的全等三角形, , , 将沿射线平移一定的距离得到 , 连接 , .若四边形是矩形,则平移的距离为.
18. 如图,和是两个具有公共边的全等三角形, , , 将沿射线平移一定的距离得到 , 连接 , .若四边形是矩形,则平移的距离为.
三、解答题
-
19.(1)、计算: ﹣( )﹣1+| ﹣2|﹣2cos45°;(2)、解不等式组: .20. 地铁为我们提供了方便、舒适、快捷的出行条件,但地铁上也有一些不文明的现象.某市记者为了解“乘坐地铁时的不文明行为”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.
组别
观点
频数(人数)
A
破坏先下后上的规矩堵进出口
80
B
占座
m
C
拒绝安检
n
D
吃东西、随手丢垃圾
120
E
其他
60

请根据图表中提供的信息解答下列问题.
(1)、填空:m= , n= , 扇形统计图中E组所占的百分比为%.(2)、若从这次接受调查的市民中随机抽出一人,则此人持C组观点的概率是多少?(3)、若该市约有100万人,请你估计其中持D组观点的人数.21. 如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30º,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,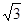 ≈1.73)
≈1.73) 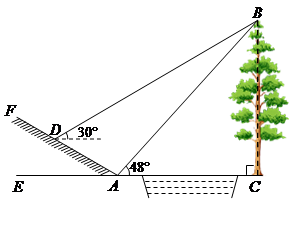 22. 如图,点C是以O为圆心,为直径的半圆上一动点(不与A,B重合), , 连接并延长至点D,使 , 过点D作的垂线 , 分别交 , , 于点E,F,H,连接.记 , 随点C的移动而变化.
22. 如图,点C是以O为圆心,为直径的半圆上一动点(不与A,B重合), , 连接并延长至点D,使 , 过点D作的垂线 , 分别交 , , 于点E,F,H,连接.记 , 随点C的移动而变化.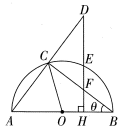 (1)、当时,求证:;(2)、连接 , 当时,求的长.23. 如图,已知一次函数与反比例函数的图象相交于 , B两点,过点B作轴于点C,连接.
(1)、当时,求证:;(2)、连接 , 当时,求的长.23. 如图,已知一次函数与反比例函数的图象相交于 , B两点,过点B作轴于点C,连接. (1)、求k,b的值和B点坐标;(2)、将沿x轴向右平移,对应得到 , 当反比例函数图象经过的中点M时,求的面积;(3)、在第一象限内的双曲线上求一点P,使得.24. 某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
(1)、求k,b的值和B点坐标;(2)、将沿x轴向右平移,对应得到 , 当反比例函数图象经过的中点M时,求的面积;(3)、在第一象限内的双曲线上求一点P,使得.24. 某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元. (1)、经调查,该蔬菜经销商销售该种蔬菜的日销售量y(千克)与零售价x(元/千克)为一次函数关系,其图象如图所示,求y与x之间的函数关系式;(2)、若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,则零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?25. 如图,已知抛物线与x轴交于点A和点 , 与y轴交于点 , 连接 , , 点P是抛物线第一象限上的一动点,过点P作轴于点D,交于点E.
(1)、经调查,该蔬菜经销商销售该种蔬菜的日销售量y(千克)与零售价x(元/千克)为一次函数关系,其图象如图所示,求y与x之间的函数关系式;(2)、若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,则零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?25. 如图,已知抛物线与x轴交于点A和点 , 与y轴交于点 , 连接 , , 点P是抛物线第一象限上的一动点,过点P作轴于点D,交于点E.

 (1)、求抛物线的函数表达式;(2)、如图1,作于点P,使 , 以 , 为邻边作矩形.当矩形的面积与的面积相等时,求点P的坐标;(3)、如图2,当点P运动到抛物线的顶点时,点Q在直线上,若为钝角,请直接写出点Q纵坐标n的取值范围.26. 如图1,在正方形中, , 点E是射线上一动点,连接 , 以为边在上方作正方形 , 连接 , , 交于点H.
(1)、求抛物线的函数表达式;(2)、如图1,作于点P,使 , 以 , 为邻边作矩形.当矩形的面积与的面积相等时,求点P的坐标;(3)、如图2,当点P运动到抛物线的顶点时,点Q在直线上,若为钝角,请直接写出点Q纵坐标n的取值范围.26. 如图1,在正方形中, , 点E是射线上一动点,连接 , 以为边在上方作正方形 , 连接 , , 交于点H. (1)、求证:;(2)、如图2,延长 , , 交于点M.若 , 求线段的长;(3)、在点E的运动过程中,求的最小值.
(1)、求证:;(2)、如图2,延长 , , 交于点M.若 , 求线段的长;(3)、在点E的运动过程中,求的最小值.