陕西省西安市蓝田县2022年九年级中考二模数学试卷

试卷更新日期：2022-06-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，立方根不等于它本身的是（）

A、2 B、1 C、0 D、－1

查看试题解析
2. 长城被誉为“世界中古七大奇迹之一”，它的全长超过21000千米，数据21000用科学记数法表示为（）

A、 $2.1 \times 1 0^{4}$ B、 $21 \times 1 0^{4}$ C、 $2.1 \times 1 0^{5}$ D、 $21 \times 1 0^{5}$

查看试题解析
3. 如图，在第24届北京冬奥会的口号“一起向未来”五个字及会徽被分开印刷在一个正方体的六个面上，其平面展开图如图所示，那么在该正方体中与北京冬奥会会徽相对的面上的字是（）

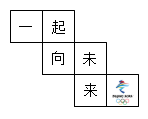A、一 B、起 C、向 D、未

查看试题解析
4. 当光线从空气中射入某种液体中时，光线的传播方向发生了变化，在物理学中这种现象叫做光的折射.如图， $A B ⊥$ 液面MN于点D，一束光线沿CD射入液面，在点D处发生折射，折射光线为DE，点F为CD的延长线上一点，若入射角 $∠ 1 = 50 °$ ，折射角 $∠ 2 = 36 °$ ，则 $∠ E D F$ 的度数为（）

A、14° B、16° C、18° D、25°

查看试题解析
5. 在如图所示的正方形网格中，每个小正方形的边长均为1， $△$ ABC的顶点A、B、C均在格点上，BD是AC边上的中线，则BD的长为（）

A、 $\sqrt{2}$ B、1.5 C、 $\sqrt{3}$ D、2.5

查看试题解析
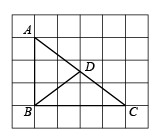6. 已知一次函数 $y = k x + b (k \neq 0)$ ，函数值y随自变量x的增大而减小，且 $k + b > 0$ ，则函数 $y = k x + b$ 的图象经过的象限是（）

A、第一、二、三象限 B、第一、三、四象限 C、第一、二、四象限 D、第二、三、四象限

查看试题解析
7. 如图，在菱形ABCD中， $∠ A = 120 °$ ，点P为边AB上一点（点P不与端点重合），连接CP，点E、F分别为AP、CP的中点，连接EF，若 $E F = 2$ ，则菱形ABCD的面积为（）

A、8 B、 $8 \sqrt{3}$ C、9 D、 $9 \sqrt{3}$

查看试题解析
8. 已知抛物线 $y = a x^{2} + b x + m$ $(a \neq 0)$ 是由抛物线 $y = x^{2} - 2 x + m$ 向左平移2个单位得到，若点 $A (- 2 ， y_{1})$ ， $B (- 1 ， y_{2})$ ， $C (1 ， y_{3})$ 都在抛物线 $y = a x^{2} + b x + m (a \neq 0)$ 上，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 之间的大小关系是（）

A、 $y_{1} < y_{3} < y_{2}$ B、 $y_{2} < y_{1} < y_{3}$ C、 $y_{2} < y_{3} < y_{1}$ D、 $y_{1} < y_{2} < y_{3}$

查看试题解析

二、填空题

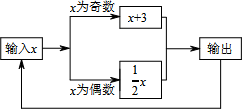
9. 请写出一个比 $\sqrt{10}$ 小的正整数．

查看试题解析
10. 若一个正多边形的半径与它的边长相等，则过该正多边形的一个顶点的对角线有条.

查看试题解析
11. 有一数值转换器，原理如图所示，若开始输入x的值是1，可发现第一次输出的结果是4，第二次输出的结果是2，……，请你探索第2021次输出的结果是.

查看试题解析
12. 如图，点A为反比例函数 $y_{1} = \frac{k_{1}}{x} (k_{1} \neq 0 ， x > 0)$ 的图象上一点，过点A作 $A B ⊥ x$ 轴于点B，作 $A D ⊥ y$ 轴于点D，反比例函数 $y_{2} = \frac{k_{2}}{x} (k_{2} \neq 0 ， x > 0)$ 的图象与AB交于点C，连接OA、OC，若 $S_{△ O A D} = 3$ ， $S_{△ O A C} = 2$ ，则 $k_{2}$ 的值为.

查看试题解析
13. 如图，点E、F为平行四边形ABCD的边BC上两点，且 $E F = \frac{1}{2} B C$ ，连接DE、AF，DE与AF相交于点P，连接PB、PC，若 $△$ PAB与 $△$ PCD的面积之和为30，则 $△$ PBE与 $△$ PCF的面积之和为.

查看试题解析

三、解答题

14. 计算： $\sqrt{24} \div \sqrt{3} + | 3 - \sqrt{8} | - \sqrt{25}$ .

查看试题解析
15. 解方程： $\frac{x}{x - 1} - 1 = \frac{2}{x}$ ．

查看试题解析
16. 解不等式 $\frac{x + 1}{3} \leq \frac{3 x - 2}{6} + 1$ ，并将其解集表示在如图所示的数轴上.

查看试题解析
17. 如图，点C为 $∠ A O B$ 的边OA上一点， $C D ⊥ O B$ 于点D，请用尺规作图法在 $∠ A O B$ 的内部作射线CE，使得 $∠ A C E + ∠ O C D = 90 °$ .（保留作图痕迹，不写作法）

查看试题解析
18. 如图，在平行四边形ABCD中，对角线AC与BD交于点O，且AC=BD，请你从①AC⊥BD、②AB=BC、③BD平分∠ABC中任选一个作为添加条件，另两个中的一个作为结论，组成一个真命题，并证明.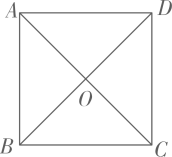

(1)、添加条件：，结论：；（填序号）

(2)、根据你所选择的条件和结论，写出证明过程.

查看试题解析
19. 《孙子算经》是我国古代重要的数学著作，其中有如下问题：今有人盗库绢，不知所失几何，但闻草中分绢，人得六匹，盈六匹；人得七匹，不足七匹.问人、绢各几何？大意是：有几个盗贼偷了仓库里的绢，不知道具体偷盗了多少匹绢，只听盗贼在草丛中分绢时说：“每人分6匹，会剩下6匹；每人分7匹，还差7匹.”问有多少盗贼？多少匹绢？

查看试题解析
20. 冰墩墩是2022年北京冬季奥运会的吉祥物，憨态可掬的外貌加上富有超能力的冰晶外壳，深受广大民众的喜爱.某商场为促进消费，举行了“玩转盘游戏，领奥运礼品”的促销活动，活动规定：将一个可自由转动的转盘平均分成4个扇形，如图，每个扇形中都有一个问题，顾客在该商场一次性消费每满300元，即可获得一次转转盘的机会.顾客转动一次转盘，转盘停止后，若将指针所指扇形中的问题回答正确，则可得到一个冰墩墩玩偶（若指针指在分界线上，则重转一次，直到指针指向某一个扇形区域为止）.已知小欣和妈妈在该商场消费600元，获得了两次转转盘机会.

(1)、小欣转动一次转盘，转盘停止后指针指向扇形A的概率为；

(2)、已知小欣只知道A、C两个问题的答案，请用列表法或画树状图的方法，求小欣转了两次转盘，至少得到一个冰墩墩玩偶的概率.

查看试题解析

21. 九年级数学“综合与实践”课的任务是测量学校旗杆的高度.晓雪和她的朋友们制定了测量方案，并完成了实地测量，测量结果如下：

课题	测量学校旗杆的高度
测量工具	测角仪和皮尺
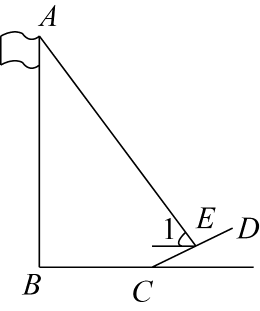
测量示意图及说明		说明：BC为水平地面，旗杆AB⊥BC，斜坡CD的坡度 $i = 1 ： 2$ ，在斜坡CD上的点E处，测得旗杆顶端A的仰角∠1的度数.
测量数据	BC=8米，CE=2 $\sqrt{5}$ 米，∠1=50.3°
参考数据	$t a n 50.3 ° \approx 1.2$

请你根据以上测量结果，计算旗杆的高度AB.

查看试题解析

22. 从黄土地上的村支书，到泱泱大国的领导人，习近平总书记始终保持劳动者本色，始终保持对劳动人民的深厚感情.总书记强调，“无论时代条件如何变化，我们始终都要崇尚劳动、尊重劳动者”.为强化劳动观念，弘扬劳动精神，某学校要求学生周末时间积极参加家务劳动，承担一定的家庭劳动，进一步培养生活自理能力和习惯，增强家庭责任意识.该学校为了解八年级同学们每周参加家务劳动时间的大致情况，从全校八年级学生中随机抽取部分学生，调查他们平均每周参加家务劳动的时间（单位：h），并对调查结果进行整理和分析，过程如下：

【收集数据】

1h	1.5h	1.5h	2h	2.5h	3h	3h	3.5h	4h	4h
4h	4.5h	5h	5h	5h	5h	5.5h	6h	6.5h	7.5h

【整理数据】

组别	A	B	C	D
时间x/h	$0 \leq x \leq 2$	$2 < x \leq 4$	$4 < x \leq 6$	$6 < x \leq 8$
人数/人	4	7	7	2

【分析数据】

平均数	中位数	众数
a	b	c

(1)、填空：上表中a= ， b= ， c=；

(2)、若该校共有500名八年级学生，请你估计其中平均每周参加家务劳动的时间不少于5h的学生有多少名？

(3)、针对平均每周参加家务劳动的时间不足2h的学生，请你为他们提出一条合理化建议.

查看试题解析

23. 近日，历经13年筹备与建设的全国首座考古学科专题博物馆——陕西考古博物馆正式建成，于4月28日至7月31日对外试行开放，它被网友称为是“中国文博又盛开的一朵美丽花朵”.五一期间，小明与晓慧两家从同一地点出发，沿同一路线分别驾车前往该博物馆参观，已知他们的出发地距离博物馆300km，图中折线 $O A - A B$ 、线段OC分别表示小明和晓慧距离出发地的路程 $y (k m)$ 与行驶时间 $x (h)$ 之间的函数关系，根据图象解答下列问题：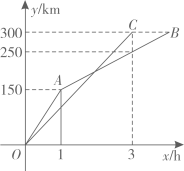

(1)、求出发1小时后，小明距离出发地的路程 $y (k m)$ 与行驶时间 $x (h)$ 之间的函数关系式；

(2)、小明和晓慧在途中相遇时，距离目的地还有多远？

查看试题解析
24. 如图，在Rt $△$ ABC中， $∠ B A C = 90 °$ ，点O为BC上一点，以O为圆心、OB为半径的⊙ $O$ 切AC于点D，连接OA、BD、OA与BD相交于点E.

(1)、求证：BD平分 $∠ A B C$ ；

(2)、若 $∠ C = 30 °$ ， ⊙ $O$ 的半径为10，求OE的长.

查看试题解析
25. 在平面直角坐标系中，点O为坐标原点，经过点 $(2 ， 9)$ 的抛物线 $y = x^{2} + b x + c$ 与y轴交于点 $A (0 ， 1)$ ，直线l为该抛物线的对称轴，点B为点A关于对称轴l的对称点，连接AB、OB.

(1)、试判断该抛物线与x轴交点的情况；

(2)、点P为对称轴l左侧抛物线上的点，过点P作 $P D ⊥ l$ 于点D，作 $P C ⊥ x$ 轴于点C，连接CD，问是否存在点P，使得 $△$ PCD与 $△$ AOB相似？若存在，求出符合条件的点P的坐标；若不存在，请说明理由.

查看试题解析
26.

(1)、【问题提出】如图1，在四边形ABCD中， $∠ A = 60 °$ ， $∠ A B C = ∠ A D C = 90 °$ ，点E为AB延长线上一点，连接EC并延长，交AD的延长线于点F，则 $∠ B C E + ∠ D C F$ 的度数为°；

(2)、【问题探究】如图2，在Rt△ABC中， $∠ A B C = 90 °$ ，点D、E在直线BC上，连接AD、AE，若 $∠ D A E = 60 °$ ， $A B = 6$ ，求△ADE面积的最小值；

(3)、【问题解决】近日，教育部印发了《义务教育课程方案和课程标准(2022年版)》，此次修订中增加的跨学科主题学习活动，突破学科边界，鼓励教师开展跨学科教研，设计出主题鲜明、问题真实的跨学科学习活动.为此，某校欲将校园内一片三角形空地ABC（如图3所示）进行扩建后作为跨学科主题学习活动中心，在AB的延长线上取一点D，连接DC并延长到点E，连接AE，已知 $A E ∥ B C$ ， $A B = B C = 40$ 米， $∠ A B C = 90 °$ ，为节约修建成本，需使修建后△ADE的面积尽可能小，问△ADE的面积是否存在最小值？若存在，求出其最小面积；若不存在，请说明理由.

查看试题解析