陕西省宝鸡市陈仓区2022年九年级中考二模数学试卷

试卷更新日期：2022-06-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，比 $- 1$ 小的数是（）

A、2 B、1 C、0 D、 $- 2$

查看试题解析
2. 右图是某个几何体的展开图，该几何体是（）

A、三棱柱 B、三棱锥 C、圆柱 D、圆锥

查看试题解析
3. 如图，直线 $a ∥ b$ ，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， AC⊥b，垂足为A，则图中与∠1互余的角有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
4. 下列计算正确的是（）

A、 $2 a - a = 1$ B、 $- 2 a^{3} \div (- a) = a^{2}$ C、 $a^{2} \cdot a^{3} = a^{6}$ D、 ${(a^{3})}^{2} = a^{6}$

查看试题解析
5. 如图，在菱形 $A B C D$ 中，对角线 $A C$ 、 $B D$ 相交于点O，若 $A C = 8$ ， $B D = 6$ ，则 $c o s ∠ A C B$ 的值（）

A、 $\frac{4}{5}$ B、 $\frac{3}{4}$ C、 $\frac{3}{5}$ D、 $\frac{4}{3}$

查看试题解析
6. 已知函数 $y = k x (k \neq 0)$ ， y随x的增大而减小，则一次函数 $y = k x - k$ 的图象经过（）

A、一，二，三象限 B、一，二，四象限 C、一，三，四象限 D、二，三，四象限

查看试题解析
7. 如图，在 $Δ A B C$ 中， $A D$ 是 $∠ B A C$ 的角平分线， $D E ⊥ A B$ 于点 $E$ ， $∠ B = 30 °$ ， $∠ C = 45 °$ ， $B E = \sqrt{3}$ ，则 $C D$ 长是（）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、2

查看试题解析
8. 已知二次函数y＝ax²+bx+c的y与x的部分对应值如下表
x
﹣1
0
1
2
y
﹣2
1
2
1
下列结论
①该函数图象是抛物线，且开口向下；
②该函数图象关于直线x＝1对称；
③当x＜1时，函数值y随x的增大而增大；
④方程ax²+bx+c＝0有一个根大于3.
其中正确的结论有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 已知实数 $- \frac{1}{2}$ ，0.16， $\sqrt{3}$ ， $π$ ， $\sqrt{25}$ ， $\sqrt[3]{4}$ ，其中为无理数的是.

查看试题解析
10. 如图，以正五边形ABCDE的对角线BE为边，作正方形BEFG，使点A落在正方形BEFG内，则∠ABG的度数为.

查看试题解析
11. 将含有30°角的直角三角板OAB如图放置在平面直角坐标系中，OB在x轴上，若OA＝2，将三角板绕原点O顺时针旋转90°，则点A的对应点A′的坐标为.

查看试题解析
12. 在反比例函数 $y = \frac{1 - 3 m}{x}$ 的图象上有两点 $A (x_{1} ， y_{1})$ 、 $B (x_{2} ， y_{2})$ ，当 $x_{1} < 0 < x_{2}$ 时，有 $y_{1} < y_{2}$ ，则m的取值范围是.

查看试题解析
13. 在 $△ A B C$ 中， $∠ A B C = 90 ° ， A B = 2 ， B C = 3$ ．点D为平面上一个动点， $∠ A D B = 45 °$ ，则线段 $C D$ 长度的最小值为．

查看试题解析

三、解答题

14. 解不等式组： ${\begin{array}{l} x - 1 \geq 0 \\ 3 - \frac{x + 1}{2} < \frac{3}{2} \end{array}$

查看试题解析
15. 计算： $\sqrt{12} \div (- \sqrt{6}) - | 4 - 3 \sqrt{2} | + {(\frac{1}{5})}^{- 1}$ .

查看试题解析
16. 化简： $\frac{m^{2} - 2 m + 1}{m^{2} - 1} \div (m - 1 - \frac{m - 1}{m + 1})$ .

查看试题解析
17. 如图，已知△ABC，AC＞AB，∠C＝45°.请用尺规作图法，在AC边上求作一点P，使∠PBC＝45°.（保留作图痕迹.不写作法）

查看试题解析
18. 如图，点 $B$ 、 $E$ 、 $F$ 、 $D$ 在同一直线上， $A B ∥ C D$ ， $A B = C D$ ， $B E = D F$ ．求证： $△ A B F ≅ △ C D E$ ．

查看试题解析
19. 一家超市中，杏的售价为11元/kg，桃的售价为10元/kg，小菲在这家超市买了杏和桃共8kg，共花费83元，求小菲这次买的杏、桃各多少千克？

查看试题解析
20. 现有A、B两个不透明的袋子，各装有三个小球，A袋中的三个小球上分别标记数字2，3，4；B袋中的三个小球上分别标记数字3，4，5.这六个小球除标记的数字外，其余完全相同.

(1)、将A袋中的小球摇匀，从中随机摸出一个小球，则摸出的这个小球上标记的数字是偶数的概率为；

(2)、分别将A、B两个袋子中的小球摇匀，然后从A、B袋中各随机摸出一个球，请利用画树状图或列表的方法，求摸出的这两个小球标记的数字之和为7的概率.

查看试题解析
21. 小宸想利用测量知识测算湖中小山的高度.他站在湖边看台上，清晰地看到小山倒映在平静的湖水中，如图所示，他在点O处测得小山顶端的仰角为45°，小山顶端A在水中倒影A′的俯角为60°.已知：点O到湖面的距离OD＝3m，OD⊥DB，AB⊥DB，A、B、A′三点共线，A'B＝AB，求小山的高度AB.（光线的折射忽略不计；结果保留根号）

查看试题解析
22. 为弘扬中华传统文化，草根一中准备开展“传统手工技艺”学习实践活动.校学生会在全校范围内随机地对本校一些学生进行了“我最想学习的传统手工技艺”问卷调查（问卷共设有五个选项：“A——剪纸”、“ B——木版画雕刻”、“ C——陶艺创作”、“ D——皮影制作”、“ E——其他手工技艺”，参加问卷调查的这些学生，每人都只选了其中的一个选项），将所有的调查结果绘制成如下两幅不完整的统计图：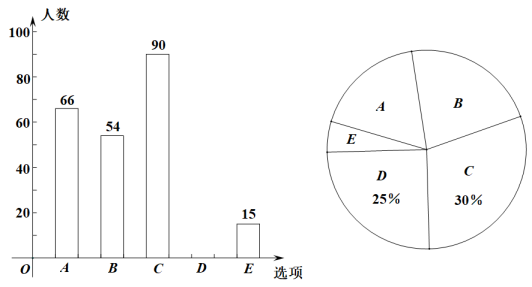
请你根据以上信息，回答下列问题：

(1)、补全上面的条形统计图；

(2)、本次问卷的这五个选项中，众数是　　；

(3)、该校共有3600名学生，请你估计该校学生“最想学习的传统手工技艺”为“A——剪纸”的人数.

查看试题解析
23. 某生物小组观察一植物生长，得到植物高度y（单位：厘米）与观察时间x（单位：天）的关系，并画出如图所示的图象（AC是线段，直线CD平行x轴）.

(1)、该植物从观察时起，多少天以后停止长高？

(2)、求直线AC的解析式，并求该植物最高长多少厘米？

查看试题解析
24. 如图，AB为 $⊙ O$ 的直径，点C在 $⊙ O$ 上，过点C作 $⊙ O$ 切线CD交BA的延长线于点D，过点O作 $O E ∥ A C$ 交切线DC于点E，交BC于点F.

(1)、求证： $∠ B = ∠ E$ ；

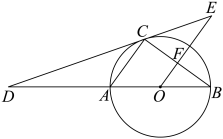(2)、若 $A B = 10$ ， $c o s B = \frac{4}{5}$ ，求EF的长.

查看试题解析
25. 在平面直角坐标系中，抛物线L：y＝﹣x²+x+2与y轴交于点C，与x轴交于A、B两点（点A在点B的左侧）.

(1)、求A、B、C三点的坐标；

(2)、连接AC、BC，以点C为位似中心，将△ABC扩大到原来的2倍得到△A₁B₁C，其中点A₁、B₁分别是点A、B的对应点，如何平移抛物线L才能使其同时经过点A₁、B₁ ，求出所有的平移方式.

查看试题解析
26.

(1)、如图1，在四边形ABCD中，点P为AB上点， $∠ D P C = ∠ A = ∠ B = 90 °$ ，若 $A P = 2$ ， $P C = 2 D P$ ，则 $B C =$ ；

(2)、如图2，四边形ABCD中， $∠ A = ∠ B = 90 °$ ， $A B = 10$ ， $A D = 13$ ，点E在线段BC上且 $B E = 6$ ，连接DE，作EF⊥DE，交AB于点F，则四边形ADEF的面积为.

(3)、某精密仪器厂接到生产一种特殊四边形金属部件的任务，部件要求：如图3，四边形ABCD中， $A B = 4$ 厘米，点C到AB的距离为5厘米， $∠ C = 90 °$ 且 $B C = 2 C D$ .在满足要求和保证质量的前提下，仪器厂希望造价最低，已知这种金属材料每平方厘米造价50元.请问一个这种四边形金属部件的造价最低是多少元？

查看试题解析

x	﹣1	0	1	2
y	﹣2	1	2	1