河南省郑州市2021-2022学年八年级下学期期中数学试卷

试卷更新日期：2022-06-10 类型：期中考试

进入出卷网下载

一、单选题

1. 2022年北京冬奥会己顺利闭幕，下列历届冬奥会会徽的部分图案中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列命题中，假命题的是（）

A、等腰三角形的两个底角相等 B、直角三角形的两个锐角互余 C、有两个内角是 60°的三角形是等边三角 D、等腰三角形的两个底角的平分线互相垂直

查看试题解析
3. 下列各式中，从左到右的变形是因式分解的是（）

A、2a²﹣2a+1＝2a（a﹣1）+1 B、（x+y）（x﹣y）＝x²﹣y² C、x²﹣4xy+4y²＝（x﹣2y）² D、x²+1＝x（x+ $\frac{1}{x}$ ）

查看试题解析
4. 在平面直角坐标系内，将点M（5，2）先向下平移2个单位，再向左平移3个单位，则移动后的点的坐标是（）

A、（2，3） B、（2，0） C、（3，5） D、（8，4）

查看试题解析
5. 我们定义一个关于实数a，b的新运算，规定：a*b＝3a－2b，例如，4*5＝3×4－2×5，若实数m满足m*2＜1，则m的取值范围是（　　）

A、 $m > \frac{3}{5}$ B、 $m > \frac{5}{3}$ C、 $m < \frac{3}{5}$ D、 $m < \frac{5}{3}$

查看试题解析
6. 如图，在△ABC中，DE是AC的垂直平分线，AC=6cm，且△ABD的周长为10cm，则△ABC的周长为（）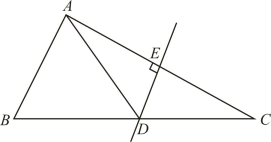

A、6cm B、10cm C、13cm D、16cm

查看试题解析
7. 如图所示：某公园里有一处长方形风景欣赏区ABCD，AB长50米，BC宽25米，为方便游人观赏，公园特意修建了如图所示的小路（图中非阴影部分），小明同学在假期沿着小路的中间行走（图中虚线），则：小明同学所走的路径长约为（）米.（小路的宽度忽略不计）

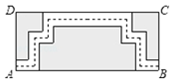A、150米 B、125米 C、100米 D、75米

查看试题解析
8. 如图，OP平分∠AOB，E为OA上一点，OE＝4，P到OB的距离是2，则△OPE的面积为（）

A、2 B、3 C、4 D、8

查看试题解析
9. 若关于x的不等式组 ${\begin{array}{l} x - m < 0 \\ 5 - 2 x < 1 \end{array}$ 的整数解共有2个，则m的取值范围是（）

A、5<m≤6 B、4<m≤5 C、5≤m<6 D、4≤m<5

查看试题解析
10. 如图，在 $△ A B C$ 中， $A B = A C = 10$ ， $B C = 16$ ，点 $D$ 是边 $B C$ 上一点（点 $D$ 不与点 $B$ ，点 $C$ 重合），将 $A C$ 绕点 $A$ 顺时针旋转至 $A C_{1}$ ， $A C_{1}$ 交 $B C$ 于点 $H$ ，且 $A D$ 平分 $∠ C A C_{1}$ ，若 $D C_{1} / / A B$ ，则点 $B$ 到线段 $A D$ 的距离为（）

A、 $2 \sqrt{10}$ B、 $\frac{7 \sqrt{10}}{2}$ C、 $4 \sqrt{5}$ D、 $3 \sqrt{10}$

查看试题解析

二、填空题

11. 已知△ABC中，AB＝AC，求证：∠B＜90°.用反证法证明，第一步是假设.

查看试题解析
12. 若 a>b，则﹣2a﹣2b.（用“<”号或“>”号填空）

查看试题解析
13. 如果 $（ m + 1 ） x^{| m |} ＞ 2$ 是一元一次不等式，则m=

查看试题解析
14. 如图，在Rt $△$ ABC中，∠C＝90°，∠A＝15°，线段AB的垂直平分线ED分别交AC、AB于点D、E，连接BD.若CD $= \sqrt{3}$ ，则AD的长为.

查看试题解析
15. 如图， $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 30 °$ ， $A B = 16$ ，点 $P$ 是 $A C$ 边上的一个动点，将线段 $B P$ 绕点 $B$ 顺时针旋转60°得到线段 $B Q$ ，连接 $C Q$ ，则在点 $P$ 运动过程中，线段 $C Q$ 的最小值为.

查看试题解析

三、解答题

16.

(1)、解不等式组： ${\begin{array}{l} \frac{1}{2} x - 1 \leq 1 \\ 5 x - 1 > 3 (x + 1) \end{array}$ ，并把解集表示在数轴上。

(2)、因式分解：2a²x²+4a²xy+2a²y².

查看试题解析
17. 已知：如图，在△ABC中，∠ABC、∠ACB的平分线相交于点O，且MN∥BC，分别交AB、AC于点M、N.求证：MN＝BM+CN.

查看试题解析
18. 如果一元一次方程的根是一元一次不等式组的解，则称该一元一次方程为该不等式组的关联方程.

(1)、在方程①3x﹣1＝0；② $\frac{2}{3} x$ +1＝0；③x﹣（3x+1）＝﹣5 中，不等式组 ${\begin{array}{l} - x + 2 > x - 5 \\ 3 x - 1 > - x + 2 \end{array}$ 关联方程是（填序号）.

(2)、若不等式组 ${\begin{array}{l} x - \frac{1}{2} < 1 \\ 1 + x > - 3 x + 2 \end{array}$ 的一个关联方程的根是整数，则这个关联方程可以是（写出一个即可）.

查看试题解析
19. 如图，在平面直角坐标系xOy中，△ABC 的三个顶点坐标分别为 A（﹣4，1），B（﹣2，2），C（﹣3，4）（每个方格的边长均为1个单位长度）.

⑴将△ABC 平移，使点 B 移动到点 B₁ ，请画出△A₁B₁C₁；

⑵作出△ABC 关于 O 点成中心对称的△A₂B₂C₂ ，并直接写出A₂ ， B₂ ， C₂的坐标；

⑶△A₁B₁C₁与△A₂B₂C₂是否成中心对称？若是，请直接写出称中心的坐标；若不是，请说明理由.

查看试题解析
20. 如图，△ABC 中，AD 是∠BAC 的平分线，DE⊥AB，DF⊥AC，E、F 为垂足，连接 EF 交 AD于G.

(1)、求证：AE＝AF.

(2)、试判断 AD 与 EF 的位置关系，并说明理由.

查看试题解析
21. 直线y₁＝﹣x＋3和直线y₂＝kx﹣2分别交y轴于点A、B，两直线交于点C（2，m）.

(1)、求m，k的值；

(2)、求△ABC的面积；

(3)、根照图象直接写出当y₁＞y₂自变量x的取值范围.

查看试题解析
22. 某汽车租赁公司要购买轿车和面包车共10辆，其中轿车至少要购买3辆，轿车每辆12万元，面包车每辆8万元，公司可投入的购车款不超过100万元；

(1)、符合公司要求的购买方案有几种？请说明理由；

(2)、如果每辆轿车的日租金为250元，每辆面包车的日租金为150元，假设新购买的这10辆车每日都可租出，要使这10辆车的日租金不低于2000元，那么应选择以上哪种购买方案？

查看试题解析
23. 在△ABC中AB=AC，点P在平面内，连接AP并将线段AP绕点A顺时针方向旋转与∠BAC相等的角度，得到线段AQ，连接BQ；

【发现问题】如图1，如果点P是BC边上任意一点，则线段BQ和线段PC的数量关系是 ▲ ；

【探究猜想】如图2，如果点P为平面内任意一点，前面发现的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由.请仅以图2所示的位置关系加以证明（或说明）；

【拓展应用】如图3，在△ABC中，AC=2，∠ACB=90°，∠ABC=30°，P是线段BC上的任意一点连接AP，将线段AP绕点A顺时针方向旋转60°，得到线段AQ，连接CQ，请直接写出线段CQ长度的最小值.

查看试题解析