河南省信阳市潢川县2021-2022学年八年级下学期期中数学试卷

试卷更新日期：2022-06-10 类型：期中考试

进入出卷网下载

一、单选题

1. 二次根式 $\sqrt{x - 3}$ 中的x最小只能是（）

A、－3 B、0 C、 $\sqrt{3}$ D、3

查看试题解析
2. 下列运算结果正确的是（）

A、 $\sqrt{3} + \sqrt{3} = \sqrt{6}$ B、 $6 \div \sqrt{6} = \sqrt{6}$ C、 $\sqrt{(- 6)^{2}} = \sqrt{6}$ D、 $\sqrt{12} \times \frac{1}{2} = \sqrt{6}$

查看试题解析
3. 斜边长是4的直角三角形，它的两条直角边可能是（）

A、3， $\sqrt{7}$ B、2，3 C、3，5 D、2，2

查看试题解析
4. 下列关于 $2 \sqrt{6}$ 的表述错误的是（）

A、 $2 \sqrt{6}$ 是最简二次根式 B、 $2 \sqrt{6}$ 是无理数 C、 $2 \sqrt{6}$ 就是 $2 \times \sqrt{6}$ D、 $2 \sqrt{6}$ 大于5

查看试题解析
5. 如图，在平行四边形ABCD中，AC与BD相交于点O，则下列结论不一定成立的是（）

A、 $O A = O C$ B、 $C D = A B$ C、 $∠ D A C = ∠ C A B$ D、 $A D ∥ B C$

查看试题解析
6. 数学课上，老师要同学们判断一个四边形门框是否为矩形.下面是某合作小组的4位同学拟定的方案，其中正确的是（）

A、测量对角线是否互相平分 B、测量两组对边是否分别相等 C、测量一组邻边是否相等 D、测量三个角是否为直角

查看试题解析
7. 如图，在矩形COED中，点D的坐标是(1，3)，则CE的长是（）

A、3 B、 $2 \sqrt{2}$ C、 $\sqrt{10}$ D、4

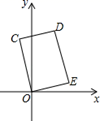查看试题解析
8. 已知实数a在数轴上的对应点位置如图所示，则化简 $| a - 1 | - \sqrt{{(a - 2)}^{2}}$ 的结果是（）

A、 $3 - 2 a$ B、-1 C、1 D、 $2 a - 3$

查看试题解析
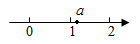9. 如图所示，一架长5m的梯子（AB），斜靠在与地面（OM）垂直的墙（ON）上，这时梯子的顶端A距地面4m.梯子的正中间P点处有一只老鼠，梯子顶端A的正下方墙角O处有一只猫.下列说法错误的是（）

A、梯子的底端B到墙的距离为3m B、P处的老鼠离地面的距离为2m C、梯子顶端沿墙下滑的长度和梯子底端沿地面向右滑行的距离不一定相等 D、梯子下滑的时候老鼠就会离猫越来越近

查看试题解析
10. 如图，矩形ABCD中，对角线AC的垂直平分线EF分别交BC、AD于点E、F，若BE=3，AF=5，则矩形ABCD的周长为（）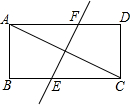

A、24 B、16 C、12 D、8

查看试题解析

二、填空题

11. 代数式 $\sqrt{2 x - 1}$ 的最小值为.

查看试题解析
12. 当a＜0时，化简 $\sqrt{0.5 a^{2}} =$ .

查看试题解析
13. 如图，已知四边形ABCD是平行四边形，下列结论中：①当 $A B = B C$ 时，它是菱形；②当 $A C ⊥ B D$ 时，它是菱形；③当 $∠ A B C = 90 °$ 时，它是矩形；④当 $A C = B D$ 时，它是正方形，正确的有.

查看试题解析
14. 如图，在▱ABCD中，AB=BC=5，对角线BD=8，则▱ABCD的面积为.

查看试题解析
15. 如图，在平面直角坐标系中，长方形MNPQ的顶点M，N分别在x轴，y轴正半轴上滑动，顶点P、Q在第一象限，若MN=10，PN＝4，在滑动过程中，点P与坐标原点O的距离的最大值为.

查看试题解析

三、解答题

16. 计算：

(1)、 $(\sqrt{24} + \sqrt{\frac{1}{6}}) \div \sqrt{6}$

(2)、 $2 \sqrt{12} - \frac{3}{\sqrt{3}} + \sqrt{27}$

查看试题解析
17. 下面是小明设计的作矩形ABCD的尺规作图过程.
已知：Rt△ABC中，∠ABC=90°
求作：矩形ABCD.

作法：如图，
1.以点A为圆心，BC长为半径作弧；
2.以点C为圆心，AB长为半径作弧；
3.两弧交于点D.点B和点D在AC异侧；
连接AD，CD.
所以四边形ABCD是矩形.

(1)、根据小明设计的尺规作图过程，使用直尺和圆规，补全图形（保留作图痕迹）；

(2)、完成下面的证明.
证明：

∵AB=①      ▲       ， BC=②      ▲       ，

∴四边形ABCD是平行四边形(③      )(填推理的依据)

又∵∠ABC=90°，

∴四边形ABCD是矩形. (④      )(填推理的依据)

查看试题解析
18. 如图，E，F，G，H分别是四边形ABCD的边AB，BC，CD，DA的中点.

(1)、判断四边形EFGH的形状，并证明你的结论；

(2)、当BD，AC满足时，四边形EFGH是菱形.

查看试题解析
19. 在矩形ABCD中，点E在BC上，AE=AD，DF⊥AE，垂足为F．

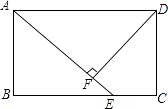(1)、求证．DF=AB；

(2)、若∠FDC=30°，且AB=4，求AD．

查看试题解析
20. 如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点.

(1)、在图1中以格点为顶点画一个面积为5的正方形.

(2)、①在图2中以格点为顶点画一个三角形，使三角形三边长分别为 $\sqrt{10}$ 、 $2 \sqrt{5}$ 、 $\sqrt{10}$ ，
②判断此三角形的形状并求出它的面积.

查看试题解析
21. 阅读并完成下面问题：
① $\frac{1}{1 + \sqrt{2}} = \frac{1 \times (\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$ ；
② $\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$ ；
③ $\frac{1}{\sqrt{5} + \sqrt{3}} = \frac{\sqrt{5} - \sqrt{3}}{(\sqrt{5} + \sqrt{3}) (\sqrt{5} - \sqrt{3})} = \frac{\sqrt{5} - \sqrt{3}}{2}$ .
试求：

(1)、下列各数中，与 $2 - \sqrt{3}$ 的积是有理数的是____.

A、 $2 + \sqrt{3}$ ； B、2； C、 $\sqrt{3}$ ； D、 $2 - \sqrt{3}$

(2)、 $\sqrt{7} + \sqrt{6}$ 的倒数为.

(3)、若 $x = \frac{1}{\sqrt{2} - 1}$ ，求 $x^{2} - 2 x$ 的值.

查看试题解析
22. 定义：有一个内角为90°，且对角线相等的四边形称为准矩形.

(1)、如图1，准矩形ABCD中，∠ABC＝90°，若AB＝2，BC＝4，则BD＝；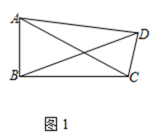

(2)、如图2，正方形ABCD中，点E，F分别是边AD，AB上的点，且CF⊥BE，求证：四边形BCEF是准矩形；

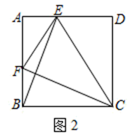(3)、如图3，准矩形ABCD中，∠ABC＝90°，∠BAC＝60°，AB＝2，AC＝DC，求这个准矩形的面积.

查看试题解析
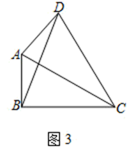23. 已知在菱形ABCD中，点P在CD上，连接AP.

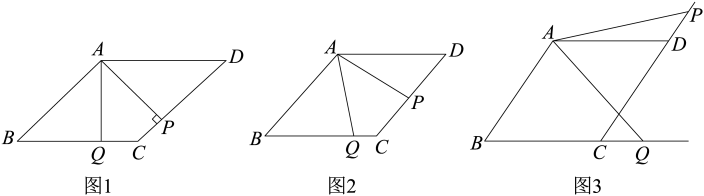(1)、在BC上取点Q，使得 $∠ P A Q = ∠ B$ ，
①如图1，当 $A P ⊥ C D$ 于点P时，线段AP与AQ之间的数量关系是 ▲

②如图2，当AP与CD不垂直时，判断①中的结论是否仍然成立，若成立，请给出证明，若不成立，则需说明理由.

(2)、若P、Q分别在CD和BC的延长线上，当 $∠ P A Q = ∠ B$ 时，CQ和DP会不会相等？如能相等请直接写出此时∠B应满足的条件，如不能相等则说明理由.

查看试题解析