重庆市云阳县“梯城教育联盟”2021-2022学年七年级下学期期中教学效果评估数学试卷
试卷更新日期:2022-06-10 类型:期中考试
一、单选题
-
1. 在-2, 0,1,-4,这四个数中,最大的数是( )A、-4 B、-2 C、0 D、12. 在 , , , , , 3.212212221…(每相邻两个1之间依次多一个2),3.14这些数中,无理数的个数为( )A、5 B、2 C、3 D、43. 如图所示的象棋盘上,若“帅”位于点(1,-2)上,“象”位于点(3,-2)上,则“炮”位于点( )
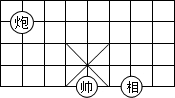 A、(1,-2) B、(-2,1) C、(-2,2) D、(2,-2)4. 将点A(-1,2)向右平移3个单位长度,再向下平移5个单位长度,则平移后点的坐标是( )A、(2,3) B、(-2,-3) C、(2,-3) D、(-2,3)5. 点P(x﹣1,x+1)不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 点A(-4,-5),点B(-6,-5),则AB等于( )A、4 B、2 C、5 D、37.
A、(1,-2) B、(-2,1) C、(-2,2) D、(2,-2)4. 将点A(-1,2)向右平移3个单位长度,再向下平移5个单位长度,则平移后点的坐标是( )A、(2,3) B、(-2,-3) C、(2,-3) D、(-2,3)5. 点P(x﹣1,x+1)不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 点A(-4,-5),点B(-6,-5),则AB等于( )A、4 B、2 C、5 D、37.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
 A、30° B、25° C、20° D、15°8. 下列说法正确的是( )A、有且只有一条直线与已知直线平行 B、垂直于同一条直线的两条直线互相垂直 C、从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离 D、在平面内过一点有且只有一条直线与已知直线垂直9. 如果是方程组的解,则a、b的值是( )A、 B、 C、 D、10. 坐标平面内有一点 ,且点A到x轴的距离为3,到y轴的距离恰为到x轴距离的2倍.若 ,则点A的坐标为( )A、(6,-3) B、(-6,3) C、(3,-6)或(-3,6) D、(6,-3)或(-6,3)11. 计算 的值为( )A、 B、 C、 D、12. 如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A4n+1(n是自然数)的坐标为( )
A、30° B、25° C、20° D、15°8. 下列说法正确的是( )A、有且只有一条直线与已知直线平行 B、垂直于同一条直线的两条直线互相垂直 C、从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离 D、在平面内过一点有且只有一条直线与已知直线垂直9. 如果是方程组的解,则a、b的值是( )A、 B、 C、 D、10. 坐标平面内有一点 ,且点A到x轴的距离为3,到y轴的距离恰为到x轴距离的2倍.若 ,则点A的坐标为( )A、(6,-3) B、(-6,3) C、(3,-6)或(-3,6) D、(6,-3)或(-6,3)11. 计算 的值为( )A、 B、 C、 D、12. 如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A4n+1(n是自然数)的坐标为( )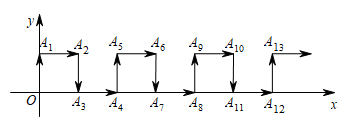 A、(1,2n) B、(2n,1) C、(n,1) D、(2n-1,1)
A、(1,2n) B、(2n,1) C、(n,1) D、(2n-1,1)二、填空题
-
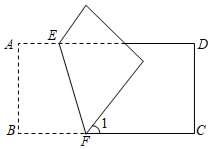
13. 的平方根是14. 若方程是二元一次方程,则.15. 若y= + +4,则x2+y2的算术平方根是 .16. 如图,把长方形ABCD沿EF对折,若∠1=50°,则∠AEF的度数等于.
三、解答题
-
17. 计算:(1)、(2)、4x2-16=018. 求解:(1)、27(x-3)3=-64(2)、19. 若5a+1和a-19是数m的平方根,求m的值.20. 实数a,b在数轴上的对应点A,B的位置如图所示,且|a|=2,b是16的一个平方根,求式子|a+b|--的值.
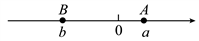 21. 如图,在平面直角坐标系中,已知 是三角形 的边 上的一点,把三角形 经过平移后得三角形 ,点 的对应点为
21. 如图,在平面直角坐标系中,已知 是三角形 的边 上的一点,把三角形 经过平移后得三角形 ,点 的对应点为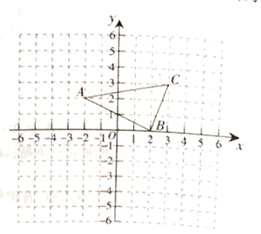 (1)、写出 三点的坐标;(2)、画出三角形 ;(3)、求三角形 的面积.22.
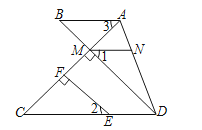
(1)、写出 三点的坐标;(2)、画出三角形 ;(3)、求三角形 的面积.22.已知,如图,EF⊥AC于F,DB⊥AC于M,∠1=∠2,∠3=∠C,求证:AB∥MN.
 23. 解方程组
23. 解方程组解:设 ,
原方程组可以化为
解得
即:此种解方程组的方法叫换元法.
(1)、运用上述方法解下列方程组;(2)、已知关于x,y的方程组的解为 , 求关于m、n的方程组的解.24.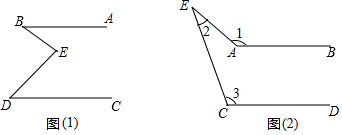 (1)、如图①,若∠B+∠D=∠BED,试猜想AB与CD的位置关系,并说明理由;(2)、如图②,要想得到AB∥CD,则∠1、∠2、∠3之间应满足怎样的数量关系,试说明理由.25. 如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D.连接AC,BD.
(1)、如图①,若∠B+∠D=∠BED,试猜想AB与CD的位置关系,并说明理由;(2)、如图②,要想得到AB∥CD,则∠1、∠2、∠3之间应满足怎样的数量关系,试说明理由.25. 如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D.连接AC,BD.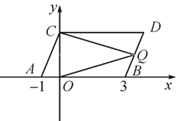 (1)、写出点C,D的坐标及四边形ABDC的面积.(2)、在y轴上是否存在一点P,连接PA,PB,使S三角形PAB=S四边形ABDC?若存在,求出点P的坐标,若不存在,试说明理由;(3)、点Q是线段BD上的动点,连接QC,QO,当点Q在BD上移动时(不与B,D重合),给出下列结论:①的值不变;②的值不变,其中有且只有一个正确,请你找出这个结论并求值.
(1)、写出点C,D的坐标及四边形ABDC的面积.(2)、在y轴上是否存在一点P,连接PA,PB,使S三角形PAB=S四边形ABDC?若存在,求出点P的坐标,若不存在,试说明理由;(3)、点Q是线段BD上的动点,连接QC,QO,当点Q在BD上移动时(不与B,D重合),给出下列结论:①的值不变;②的值不变,其中有且只有一个正确,请你找出这个结论并求值.