江苏省南通市启东市2021-2022学年七年级下学期期中数学试卷
试卷更新日期:2022-06-10 类型:期中考试
一、单选题
-
1. 下列生活现象中,属于平移的是( )A、升降电梯的上下移动 B、荡秋千运动 C、把打开的课本合上 D、钟摆的摆动2. 在实数 , , , 3.1415926,2.1313313331…(每两个1之间依次多1个3)中,其中是无理数的有( )A、1个 B、2个 C、3个 D、4个3. 点P(3,﹣4)在平面直角坐标系中所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 如图,直线a,b被c,d所截,且c⊥a,c⊥b,∠1=57°,则∠2的度数为( )
 A、113° B、120° C、123° D、147°5. 下列式子中错误的是( )A、 B、 C、 D、6. 如图,点E在AC的延长线上,下列条件能判断AB∥CD的是( )
A、113° B、120° C、123° D、147°5. 下列式子中错误的是( )A、 B、 C、 D、6. 如图,点E在AC的延长线上,下列条件能判断AB∥CD的是( ) A、∠1=∠2 B、∠3=∠4 C、∠D=∠DCE D、∠D+∠ACD=180°7. 如图,数轴上的点A,B,O,C,D分别表示数-2,-1,0,1,2,则表示数的点P应落在( )
A、∠1=∠2 B、∠3=∠4 C、∠D=∠DCE D、∠D+∠ACD=180°7. 如图,数轴上的点A,B,O,C,D分别表示数-2,-1,0,1,2,则表示数的点P应落在( )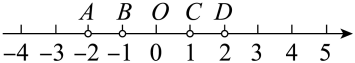 A、线段AB上 B、线段BO上 C、线段OC上 D、线段CD上8. 已知 ,则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是( )
A、线段AB上 B、线段BO上 C、线段OC上 D、线段CD上8. 已知 ,则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是( )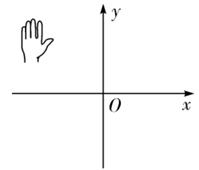 A、 B、 C、 D、9. 如图, ,直线 分别交 , 于点E,F, 平分 ,若 ,则 的大小是( )
A、 B、 C、 D、9. 如图, ,直线 分别交 , 于点E,F, 平分 ,若 ,则 的大小是( )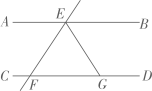 A、 B、 C、 D、10. 如图,在平面直角坐标系xOy中,点A坐标是(1,1).若记点A坐标为 , 则一个点从点A出发沿图中路线依次经过 , , …,每个点的横纵坐标都是整数,按此规律一直运动下去,则的值为( )
A、 B、 C、 D、10. 如图,在平面直角坐标系xOy中,点A坐标是(1,1).若记点A坐标为 , 则一个点从点A出发沿图中路线依次经过 , , …,每个点的横纵坐标都是整数,按此规律一直运动下去,则的值为( )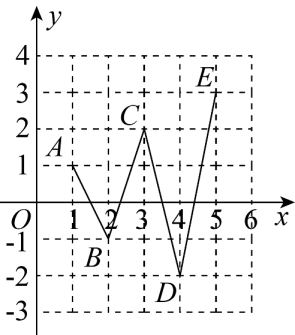 A、2021 B、2022 C、1011 D、1012
A、2021 B、2022 C、1011 D、1012二、填空题
-
11. 的立方根是 .12.
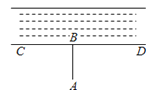
如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是
 13. 已知:若 ≈1.910, ≈6.042,则 ≈ .
13. 已知:若 ≈1.910, ≈6.042,则 ≈ .
14. 已知点A(m+1,2)和点B(3,m-1),若直线轴,则m的值为.15. 如图, , , 若∠B=72°,则∠D的度数是.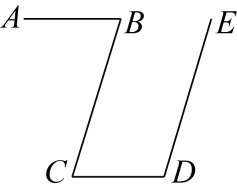 16. 一副三角板按如图所示(共顶点A)叠放在一起,若固定三角板AOB,改变三角板ACD的位置(其中A点位置始终不变),则当∠BAD=°时,.
16. 一副三角板按如图所示(共顶点A)叠放在一起,若固定三角板AOB,改变三角板ACD的位置(其中A点位置始终不变),则当∠BAD=°时,.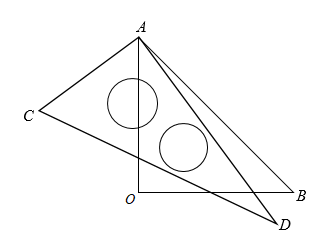 17. 如图,在平面直角坐标系中,动点P从原点O出发,水平向左平移1个单位长度,再竖直向下平移1个单位长度得到点;接着水平向右平移2个单位长度,再竖直向上平移2个单位长度得到点;接着水平向左平移3个单位长度,再竖直向下平移3个单位长度得到点;接着水平向右平移4个单位长度,再竖直向上平移4个单位长度得到点 , …,按此作法进行下去,则点的坐标为 .
17. 如图,在平面直角坐标系中,动点P从原点O出发,水平向左平移1个单位长度,再竖直向下平移1个单位长度得到点;接着水平向右平移2个单位长度,再竖直向上平移2个单位长度得到点;接着水平向左平移3个单位长度,再竖直向下平移3个单位长度得到点;接着水平向右平移4个单位长度,再竖直向上平移4个单位长度得到点 , …,按此作法进行下去,则点的坐标为 .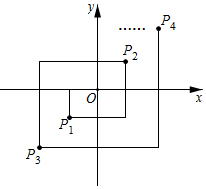 18. 对于任意两个正数x和y,规定“☆” , 例如,.请计算.
18. 对于任意两个正数x和y,规定“☆” , 例如,.请计算.三、解答题
-
19. 计算:(1)、(2)、20. 已知,在平面直角坐标系中,三角形ABC的三个顶点的坐标分别是A(-4,0),B(-2,3),C(0,-2).请回答下列问题:
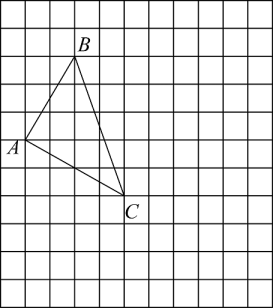 (1)、在所给的图中,画出该平面直角坐标系xOy;(2)、将三角形ABC先向右平移5个单位,再向下平移1个单位得到三角形 , , , 分别是A,B,C的对应点,画出三角形 , 并写出点 , , 的坐标;(3)、若三角形ABC内部一点P的坐标为(a,b),求平移后点P的对应点的坐标.21. 如图,AB⊥BF,CD⊥BF,∠1=∠2,试说明∠3=∠E.
(1)、在所给的图中,画出该平面直角坐标系xOy;(2)、将三角形ABC先向右平移5个单位,再向下平移1个单位得到三角形 , , , 分别是A,B,C的对应点,画出三角形 , 并写出点 , , 的坐标;(3)、若三角形ABC内部一点P的坐标为(a,b),求平移后点P的对应点的坐标.21. 如图,AB⊥BF,CD⊥BF,∠1=∠2,试说明∠3=∠E.
证明:∵AB⊥BF,CD⊥BF(已知),
∴∠ABD=∠CDF= ( ),
∴ ( )
∵∠1=∠2(已知),
∴ ( )
∴ ( )
∴∠3=∠E( )
22. 如图,直线AB,CD相交于点O,∠AOD=2∠BOD+60°. (1)、求∠BOD的度数;(2)、以O为端点引射线OE,OF,射线OE平分∠BOD,且∠EOF=90°,求∠BOF的度数.23. 已知的立方根是 , 的算术平方根是3,是的整数部分.(1)、求、、的值;(2)、求的平方根.24. 小明想用一块面积为的正方形纸片,沿边的方向裁出一块面积为的长方形纸片,使它的长宽之比为3:2,他能裁出吗?25. 已知,直线 , 直线和 , 分别交于C,D点,点A,B分别在直线 , 上,且位于直线的左侧,动点P在直线上,且不和点C,D重合.
(1)、求∠BOD的度数;(2)、以O为端点引射线OE,OF,射线OE平分∠BOD,且∠EOF=90°,求∠BOF的度数.23. 已知的立方根是 , 的算术平方根是3,是的整数部分.(1)、求、、的值;(2)、求的平方根.24. 小明想用一块面积为的正方形纸片,沿边的方向裁出一块面积为的长方形纸片,使它的长宽之比为3:2,他能裁出吗?25. 已知,直线 , 直线和 , 分别交于C,D点,点A,B分别在直线 , 上,且位于直线的左侧,动点P在直线上,且不和点C,D重合.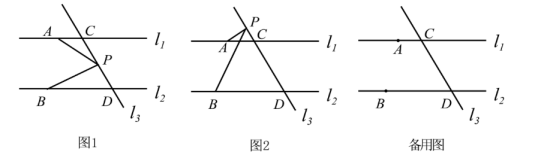 (1)、如图1,当动点P在线段CD上运动时,求证:∠APB=∠CAP+∠DBP;(2)、如图2,当动点P在点C上方运动时(P,A,B不在同一直线上),请写出∠APB,∠CAP,∠DBP之间的数量关系,并选择其中一种的数量关系说明理由.26. 规定:如果图形是由图形G经过平移所得,那么把图形称为图形G的“友好图形”,两个图形上对应点的距离称为图形与G的“友好距离”
(1)、如图1,当动点P在线段CD上运动时,求证:∠APB=∠CAP+∠DBP;(2)、如图2,当动点P在点C上方运动时(P,A,B不在同一直线上),请写出∠APB,∠CAP,∠DBP之间的数量关系,并选择其中一种的数量关系说明理由.26. 规定:如果图形是由图形G经过平移所得,那么把图形称为图形G的“友好图形”,两个图形上对应点的距离称为图形与G的“友好距离”在平面直角坐标系xOy中,已知点A(3,0).
 (1)、①如图1,若点A的“友好图形”点B(3,6),则点A与点B的“友好距离”是 ▲ ;
(1)、①如图1,若点A的“友好图形”点B(3,6),则点A与点B的“友好距离”是 ▲ ;②若点A的“友好图形”点在y轴上,则点A与点的“友好距离”最小值为 ▲ ;
(2)、若点A的“友好图形”点C在x轴上,点A与点C的“友好距离”是4,点D在y轴上,且三角形ACD的面积为10,求点D的坐标;(3)、如图3,若点E(0,6),直线AE的“友好图形”直线恰好过点F(0,-2),且点A的“友好图形”点在x轴上,求点A与点的“友好距离”.