2022年高考数学真题试卷(北京卷)
试卷更新日期:2022-06-09 类型:高考真卷
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
-
1. 已知全集 ,集合 ,则 ( )A、 B、 C、 D、2. 若复数 满足 ,则 ( )A、1 B、5 C、7 D、253. 若直线 是圆 的一条对称轴,则 ( )A、 B、 C、1 D、-14. 已知函数 ,则对任意实数 ,有( )A、 B、 C、 D、5. 已知函数 ,则( )A、 在 上单调递减 B、 在 上单调递增 C、 在 上单调递减 D、 在 上单调递增6. 设 是公差不为0的无穷等差数列,则“ 为递增数列”是“存在正整数 ,当 时, ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件7. 在北京冬奥会上,国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术,为实现绿色冬奥作出了贡献,如图描述了一定条件下二氧化碳所处的状态与 和 的关系,其中 表示温度,单位是 ; 表示压强,单位是bar,下列结论中正确的是( )
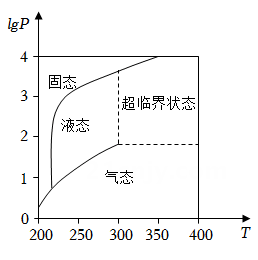 A、当 , 时,二氧化碳处于液态 B、当 , 时,二氧化碳处于气态 C、当 , 时,二氧化碳处于超临界状态 D、当 , 时,二氧化碳处于超临界状态8. 若 ,则 ( )A、40 B、41 C、-40 D、-419. 已知正三棱锥 的六条棱长均为6, 是 及其内部的点构成的集合,设集合 ,则 表示的区域的面积为( )A、 B、 C、 D、10. 在 中, , , . 为 所在平面内的动点,且 ,则 的取值范围是( )A、 B、 C、 D、
A、当 , 时,二氧化碳处于液态 B、当 , 时,二氧化碳处于气态 C、当 , 时,二氧化碳处于超临界状态 D、当 , 时,二氧化碳处于超临界状态8. 若 ,则 ( )A、40 B、41 C、-40 D、-419. 已知正三棱锥 的六条棱长均为6, 是 及其内部的点构成的集合,设集合 ,则 表示的区域的面积为( )A、 B、 C、 D、10. 在 中, , , . 为 所在平面内的动点,且 ,则 的取值范围是( )A、 B、 C、 D、二、填空题共5小题,每小题5分,共25分。
-
11. 函数 的定义域是 .12. 已知双曲线 的渐近线方程为 ,则 .13. 若函数 的一个零点为 ,则 ; .14. 设函数 ,若 存在最小值,则 的一个取值为; 的最大值为 .15. 已知数列 的各项均为正数,其前 项和 ,满足 给出下列四个结论:
① 的第2项小于3; ② 为等比数列;
③ 为递减数列; ④ 中存在小于 的项。
其中所有正确结论的序号是 .
三、解答题共6小题,共85分。
-
16. 在 中, .
(I)求 :
(II)若 ,且 的面积为 ,求 的周长.
17. 如图,在三棱柱 中,侧面 为正方形,平面 平面 , , 分别为 , 的中点.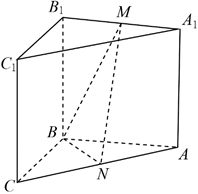
(I)求证: 平面 ;
(II)再从条件①、条件②这两个条件中选择一个作为已知,求
直线 与平面 所成角的正弦值。
条件①: ;
条件②: .
注:如果选择条件①和条件②分别解答,按第一个解答计分。
18. 在校运动会上,只有甲、乙、丙三名同学参加铅球比赛,比赛成绩达到9.50m以上(含9.50m)的同学将获得优秀奖,为预测获得优秀奖的人数及冠军得主,收集了甲、乙、丙以往的比赛成绩,并整理得到如下数据(单位:m):甲:9.80, 9.70, 9.55, 9.54, 9.48, 9.42, 9.40, 9.35, 9.30, 9.25;
乙:9.78, 9.56, 9.51, 9.36, 9.32, 9.23;
丙:9.85, 9.65, 9.20, 9.16.
假设用频率估计概率,且甲、乙、丙的比赛成绩相互独立
(I)估计甲在校运动会铅球比赛中获得优秀奖的概率;
(II)设X是甲、乙、丙在校运动会铅球比赛中获得优秀奖的总人数,估计 的数学期望 ;
(III)在校运动会铅球比赛中,甲、乙、丙谁获得冠军的概率估计值最大?(结论不要求证明)
19. 已知椭圆 的一个顶点为 ,焦距为 .(Ⅰ)求椭圆 的方程:
(Ⅱ)过点 作斜率为 的直线与椭圆 交于不同的两点 ,直线 分别与 轴交于点 ,当 时,求 的值。