(北师大版)2021-2022学年度第二学期八年级数学3.4简单的图案设计 期末复习测试卷
试卷更新日期:2022-06-08 类型:复习试卷
一、单选题
-
1. 下面四个图案中,不能由基本图案(图中阴影部分)旋转得到的是( )A、
 B、
B、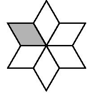 C、
C、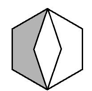 D、
D、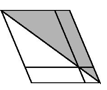 2. 如图所示的图案是由六个全等的菱形拼成的,它也可以看作是以一个图案为“基本图案”,通过旋转得到的.以下图案中,不能作为“基本图案”的一个是( )
2. 如图所示的图案是由六个全等的菱形拼成的,它也可以看作是以一个图案为“基本图案”,通过旋转得到的.以下图案中,不能作为“基本图案”的一个是( ) A、A B、B C、C D、D3. 如图是由三把相同大小的扇子展开后组成的图形,若把每把扇子的展开图看着“基本图案”那么该图形是由“基本图案”( )
A、A B、B C、C D、D3. 如图是由三把相同大小的扇子展开后组成的图形,若把每把扇子的展开图看着“基本图案”那么该图形是由“基本图案”( )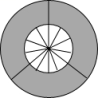 A、平移一次形成的 B、平移两次形成的 C、以轴心为旋转中心,旋转后形成的 D、以轴心为旋转中心,旋转、后形成的4. 由基本图案1得到图案2的方法是 ( )
A、平移一次形成的 B、平移两次形成的 C、以轴心为旋转中心,旋转后形成的 D、以轴心为旋转中心,旋转、后形成的4. 由基本图案1得到图案2的方法是 ( )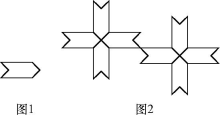 A、旋转和平移 B、中心对称和轴对称 C、平移和轴对称 D、中心对称5. 下列对下图的形成过程叙述正确的是( )
A、旋转和平移 B、中心对称和轴对称 C、平移和轴对称 D、中心对称5. 下列对下图的形成过程叙述正确的是( ) A、它可以看作是一只小狗绕图案的中心位置旋转 , , 形成的 B、它可以看作是相邻两只小狗绕图案的中心位置旋转形成的 C、它可以看作是相邻两只小狗绕图案的某条对称轴翻折而成的 D、它可以看作是左侧和上方的小狗分别向右侧和下方平移得到的6. 下列图案中,含有旋转变换的有( ) .
A、它可以看作是一只小狗绕图案的中心位置旋转 , , 形成的 B、它可以看作是相邻两只小狗绕图案的中心位置旋转形成的 C、它可以看作是相邻两只小狗绕图案的某条对称轴翻折而成的 D、它可以看作是左侧和上方的小狗分别向右侧和下方平移得到的6. 下列图案中,含有旋转变换的有( ) . A、4个 B、3个 C、2个 D、1个7.
A、4个 B、3个 C、2个 D、1个7.一个由小菱形组成的装饰链,断去了一部分,剩下部分如图所示,则断去部分的小菱形的个数可能是( )
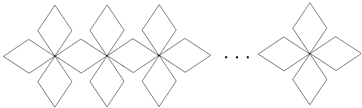 A、3 B、4 C、5 D、68. 用放大镜将图形放大,应该属于( )A、平移变换 B、相似变换 C、对称变换 D、旋转变换9.
A、3 B、4 C、5 D、68. 用放大镜将图形放大,应该属于( )A、平移变换 B、相似变换 C、对称变换 D、旋转变换9.在如图的四个三角形中,不能由△ABC经过旋转或平移得到的是( )
 A、A B、B C、C D、D10. 下列说法其中正确的个数有( )
A、A B、B C、C D、D10. 下列说法其中正确的个数有( )①能够完全重合的两个三角形是全等三角形;
②通过旋转得到的两个图形全等,全等的两个图形旋转后一定能重合;
③大小相同的两个图形是全等图形;
④一个图形经过平移、翻折、旋转后,得到的图形一定与原图形全等.
A、0个 B、1个 C、2个 D、3个二、填空题
-
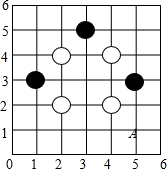
11. 如图是用围棋棋子在6×6的正方形网格中摆出的图案,棋子的位置用有序实数对表示,如A点为(5,1),若再摆一黑一白两枚棋子,使这9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是(请填写正确答案的序号)
①黑(1,5),白(5,5);②黑(3,2),白(3,3);③黑(3,3),白(3,1);④黑(3,1),白(3,3)
 12. 如果
12. 如果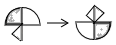 ,那么
,那么 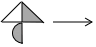 . 13. 把18个边长都为1的等边三角形如图拼接成平行四边形,且其中6个涂上了阴影,现在,可以旋转、翻折或平移某一个阴影等边三角形到某一个空白的等边三角形处,使新构成的阴影部分图案是轴对称图形,共可得种轴对称图形.
. 13. 把18个边长都为1的等边三角形如图拼接成平行四边形,且其中6个涂上了阴影,现在,可以旋转、翻折或平移某一个阴影等边三角形到某一个空白的等边三角形处,使新构成的阴影部分图案是轴对称图形,共可得种轴对称图形.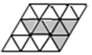 14.
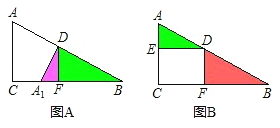
14.简述由图A变换为图B的变化过程 .
 15.
15.将图(1)中的大正方形绕着其中心顺时针至少旋转 度时,可变成图(2).

三、解答题
-
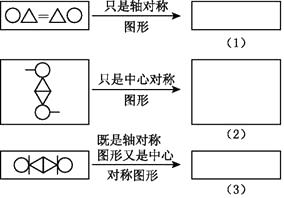
16. 以给出的图形“○,○,△,△, ”(两个相同的圆、两个相同的等边三角形、两条线段)为构件,各设计一个构思独特且有意义的轴对称图形或中心对称图形.举例:如图,左框中是符合要求的一个图形.你还能构思出其他的图形吗?请在右框中画出与之不同的图形.
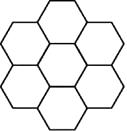
 17. 如图所示的图案是由7个正六边形组成的,下面是三名同学对该图案的形成过程的不同见解.
17. 如图所示的图案是由7个正六边形组成的,下面是三名同学对该图案的形成过程的不同见解.甲:该图案可看成是由其中一个正六边形经过6次平移而形成的.
乙:该图案可看成是由图案的一半经过轴对称变换而形成的.
丙:该图案可看成是由图案的一半经过中心对称变换而形成的.
你认为上述观点都正确吗?
 18.
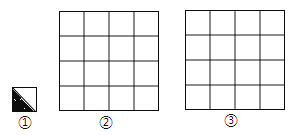
18.如图②是4×4网格,每个小正方形的边长都为1,请用图案①作为基本图案,通过平移,轴对称,旋转变换,设计两个不同的精美图案,使它们满足:①既是轴对称图形,又是中心对称图形;②所作图案用阴影标识,且阴影部分面积为4.
 19.
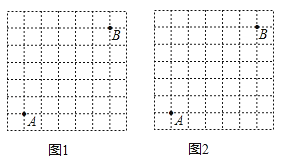
19.图1、图2分别是7×7的正方形网格,网格中每个小正方形的边长均为1,点A、B在小正方形的顶点上.
(1)在图1中确定点C、D(点C、D在小正方形的顶点上),并画出以A、B、C、D为顶点的四边形,使其是中心对称图形,但不是轴对称图形,且面积为15;
(2)在图2中确定点E、F(点E、F在小正方形的顶点上),并画出以A、B、E、F为顶点的四边形,使其既是轴对称图形,又是中心对称图形,且面积为15.
 20.
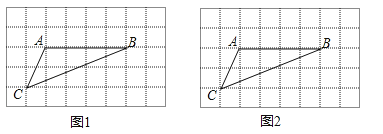
20.如图,在8×5的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在小正方形的顶点上.
(1)在图1中画△ABD(点D在小正方形的顶点上),使△ABD的周长等于△ABC的周长,且以A、B、C、D为顶点的四边形是轴对称图形.
(2)在图2中画△ABE(点E在小正方形的顶点上),使△ABE的周长等于△ABC的周长,且以A、B、C、E为顶点的四边形是中心对称图形,并直接写出该四边形的面积.
 21.
21.作图:(不写作法,但保留作图痕迹).
在平面直角坐标系中有△AOB,运用所学知识,请你设计出一把风扇形状的图案,且是中心对称图形.
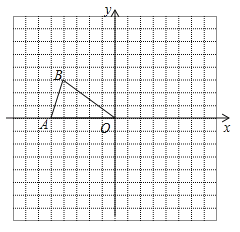 22.
22.如图,按要求涂阴影:
(1)将图形①平移到图形②;
(2)将图形②沿图中虚线翻折到图形③;
(3)将图形③绕其右下方的顶点旋转180°得到图形④.
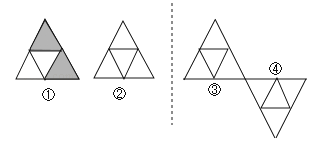 23.
23.如图1,图2,图3的网格均由边长为1的小正方形组成,图1中的团是2002年在北京举办的世界数学家大会的会标“弦图”,它既标志着中国古代的数学成就,又像一只转动着的风车,欢迎世界各地的数学家们.
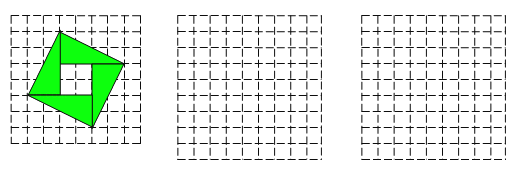
(1)图1中的“弦图”的四个直角三角形组成的图形是什么对称图形.
(2)请将“弦图”中的四个直角三角形通过你所学过的图形变换,在图2,3的方格纸中设计另外两个不同的图案,画图要求:
①每个直角三角形的顶点均在方格纸的格点上,且四个三角形互不重叠,不必涂阴影;
②图2中所设计的图案(不含方格纸)必须是轴对称图形而不是中心对称图形,图3中所设计的图案(不含方格纸)必须既是轴对称图形,又是中心对称图形.