（北师大版）2021-2022学年度第二学期八年级数学3.3中心对称 期末复习测试卷
试卷更新日期：2022-06-08 类型：复习试卷
一、单选题
-
1. 下列四个图形中，是中心对称图形的是（ ）A、
B、
C、
D、
2. 下列图形中，既是轴对称图形，又是中心对称图形的是（ ）A、
等边三角形
B、
平行四边形
C、
圆
D、
五角星
3. 习近平主席在2022年新年贺词中提到“人不负青山，青山定不负人”，一语道出“人与自然和谐共生”的至简大道.下列有关环保的四个图形中，是轴对称图形，但不是中心对称图形的是（ ）A、
B、
C、
D、
4. 栖霞市文明城市建设中，大力开展“垃圾分类”知识宣传活动，活动中推出下列图标（不包含文字），则其中是中心对称图形的是（ ）A、
B、
C、
D、
5. 下列所描述的几何图形中，既是中心对称图形，又是轴对称图形的是（ ）A、平行四边形 B、等边三角形 C、等腰三角形 D、圆6. 某校举办了“送福迎新春，剪纸庆佳节”比赛.以下参赛作品中，是中心对称图形的是（ ）.A、
B、
C、
D、
7. 如图所示，△ABC与△A'B'C'关于点O成中心对称，下列结论中不成立的是（ ）
A、OC=OC' B、AB∥A'B' C、BC=B'C' D、∠ABC=∠A'C'B'8. 已知下列命题：①成中心对称的两个图形一定全等；②成中心对称的两个图形的对应边相等并且平行；③成中心对称的两个图形的对称点的连线段被对称点平分。其中正确的是（ ）
A、①③ B、①② C、②③ D、①②③9. 下列图形中，是中心对称图形而不一定是轴对称图形的是（ ）A、平行四边形 B、矩形 C、菱形 D、等边三角形10. 下列银行标志中，是中心对称图形但不是轴对称图形的是（ ）A、
B、
C、
D、
二、填空题
-
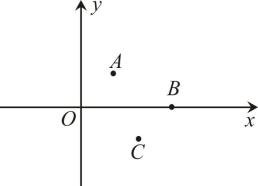
11. 如图，在平面直角坐标系中，点A，B，C的坐标分别为 ， ， ． 点M从坐标原点O出发，第一次跳跃到点 ， 使得点与点O关于点A成中心对称；第二次跳跃到点 ， 使得点与点关于点B成中心对称；第三次跳跃到点 ， 使得点与点关于点C成中心对称；第四次跳跃到点 ， 使得点与点关于点A成中心对称；…，依此方式跳跃，点的坐标是 ．
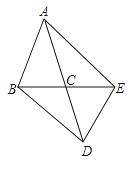
12. 如图，已知 AB=3，AC=1，∠D=90°，△DEC 与△ABC关于点C成中心对称，则AE的长是 ．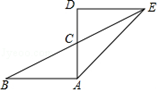
13. 已知点A（-1，2）与点B（3，4）是成中心对称的图形上的两个对称点，则对称中心的坐标为。14. 在方格纸中，选择标有序号①、②、③、④中的一个小正方形涂黑，能与图中阴影部分构成中心对称图形的小正方形的序号是。
15. 如图， 和 关于点C成中心对称，若 ， ， ，则 的长是.
三、解答题
-
16. 在平面直角坐标系xOy中的位置如图所示．
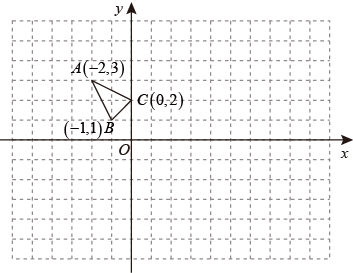
（ 1 ）作 关于点O成中心对称的 ；
（ 2 ）将 向右平移 个单位，作出平移后的 ；
（ 3 ）直接写出 各顶点坐标．
17. 如图，在 中，∠ACB=90°，M为A B的中点，∠PMQ=90° ，试判断线段PQ，AP，BQ之间的数量关系，并说明理由
18. 在艺术字中，有些汉字或字母是中心对称图形．下面的汉字或字母，是中心对称图形吗？如果是，请标出它们的对称中心．
19. 如图，长方形ABCD是篮球场的简图，请通过画图找出它的对称中心.
20. 如图，在△ABC中，∠A=90°，点D为BC的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，试写出线段BE，EF，FC之间的数量关系，并说明理由.
21.如图，已知△ABC和点求作△ABC关于点C成中心对称的△A1B1C1，保留作图痕迹，不要求写过程.
