（北师大版）2021-2022学年度第二学期八年级数学3.1图形的平移期末复习测试卷

试卷更新日期：2022-06-08 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列四组图形都含有两个可以重合的三角形，其中可以通过平移其中一个三角形得到另一个三角形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图， $R t △ A B C$ 沿直角边BC所在的直线向右平移得到 $△ D E F$ ，下列结论中错误的是（）

A、 $△ A B C$ ≌ $△ D E F$ B、 $∠ D E F = 90 °$ C、 $A C = D F$ D、 $E C = C F$

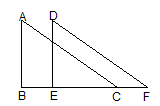查看试题解析
3. 如图，在平面直角坐标系中， $▱ A O B C$ 的顶点O与原点重合，顶点B在x轴正半轴上，顶点A的坐标为 $(- 1 ， 2)$ ．按以下步骤作图：先以点O为圆心，适当长为半径作弧，分别交边 $O A$ ， $O B$ 于点D，E；再分别以点D，E为圆心，大于 $\frac{1}{2} D E$ 的长为半径作弧，两弧在 $∠ A O B$ 内交于点F，作射线 $O F$ 交 $A C$ 边于点G．则点G的坐标为（）

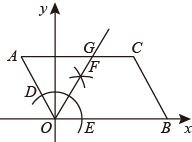A、 $(3 - \sqrt{5} ， 2)$ B、 $(\sqrt{5} ， 2)$ C、 $(\sqrt{5} - 2 ， 2)$ D、 $(\sqrt{5} - 1 ， 2)$

查看试题解析
4. 在平面直角坐标系中，要得到函数y＝2x﹣1的图象，只需要将函数y＝2x的图象（）

A、向上平移1个单位 B、向下平移1个单位 C、向左平移1个单位 D、向右平移1个单位

查看试题解析
5. 如图，△DEF是由△ABC沿射线AB方向经过平移得到的，若∠A＝33°，则∠EDF的度数为（）

A、33° B、80° C、57° D、67°

查看试题解析
6. 如图是一段台阶的截面图，高BC为5米，直角边AC为12米，现打算在台阶上铺上一整张防滑毯，至少需防滑毯的长为（）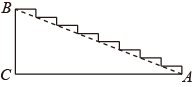

A、12米 B、13米 C、17米 D、18米

查看试题解析
7. 如图是由三个全等的菱形拼接成的图形，若平移其中一个菱形，与其他两个菱形重新拼接（无覆盖，有公共顶点），并使拼接成的图形为轴对称图形，则平移的方式共有（）

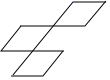A、3种 B、6种 C、8种 D、10种

查看试题解析
8. 如图，射线a、b分别与直线l交于点A、B，现将射线a沿直线l向右平移过点B，若∠1＝44°，∠2＝66°，则∠3的度数为（）

A、66° B、68° C、70° D、72°

查看试题解析
9. 如图， $Rt △ ABC$ 沿直线边BC所在的直线向右平移得到 $△ DEF$ ，下列结论中不一定正确的是 $($ $)$

A、 $∠ DEF = 90^{\circ}$ B、 $BE = CF$ C、 $CE = CF$ D、 $S_{四边形 ABEH} = S_{四边形 DHCF}$

查看试题解析
10. 在以下现象中：①用打气筒打气时，气筒里活塞的运动；②传送带上，瓶装饮料的移动；③在笔直的公路上行驶的汽车；④温度计中，液柱的上升或下降；⑤钟摆的摆动．属于平移的是（）

A、① B、①② C、①②③ D、①②③④

查看试题解析

二、填空题

11. 如图，在 $△ A B C$ 中， $B C = 5$ cm，现将 $△ A B C$ 沿射线 $B C$ 方向平移 $3 c m$ 到 $△ A^{'} B^{'} C^{'}$ 的位置，则 $B C^{'}$ 的长为．

查看试题解析
12. 如图，佳佳在玩耍时，用四个完全一样的小直角三角板按如图摆放，恰好放在一个大直角三角形内，大直角三角形的两条直角边分别为4和6，则图中四个小三角形的周长之和为．

查看试题解析
13. 已知△ABC，AB＝BC＝2cm，将△ABC向右平移3cm得到△A₁B₁C₁ ，点P、Q分别是AB、A₁B₁的中点，则PQ＝cm．

查看试题解析
14. 直线y = 3x - 2向下平移2个单位长度得到的直线是．

查看试题解析
15. 如图， $△ A B C$ 中， $A B = B C = 8 c m$ ，将 $△ A B C$ 沿 $B C$ 平移 $3 c m$ 得到 $△ D E F$ ， $A C$ 与 $D E$ 相交于点G，则 $G E$ 的长为 $c m$ ．

查看试题解析

三、解答题

16. 如图，两个单位位于一条封闭式街道的两旁，分别用点M，N表示，现准备修建一座过街天桥，桥建在何处时才能使点M到点N的路线最短?请说明理由.(注意：桥必须和街道垂直)

查看试题解析
17. 如图所示，有一条等宽的小路穿过长方形的草地ABCD，若AB=60m，BC=84m，AE=100m，则这条小路的面积是多少？

查看试题解析
18.
△ABC三个顶点的坐标分别为A（﹣2，1），B（1，2），C（0，3）．
（1）请画出△ABC，并画出它向右平移3个单位长度后得到的△A₁B₁C₁；
（2）在x轴上求作一点P，使△PAB的周长最小，请画出△PAB，并写出点P的坐标．

查看试题解析
19.
在△ABC中，∠ABC=90°，D为平面内一动点，AD=a，AC=b，其中a，b为常数，且a＜b．将△ABD沿射线BC方向平移，得到△FCE，点A、B、D的对应点分别为点F、C、E．连接BE．
（1）如图，若D在△ABC内部，请在图中画出△FCE；
（2）在（1）的条件下，若AD⊥BE，求BE的长（用含a，b的式子表示）．

查看试题解析
20.
如图，平行四边形ABCD中，点E是AD边上一点，且 CE⊥BD于点F，将△DEC沿从D到A的方向平移，使点D与点A重合，点E平移后的点记为G．
（1）画出△DEC平移后的三角形；
（2）若BC= $2 \sqrt{5}$ ， BD=6，CE=3，求AG的长．

查看试题解析
21.
如图，长方形ABCD在坐标平面内，点A的坐标是A（2，1），且边AB、CD与x轴平行，边AD、BC与y轴平行，点B、C的坐标分别为B（a，1），C（a，c），且a、c满足关系式．c= $\sqrt{a - 6}$ + $\sqrt{6 - a}$ +3
（1）求B、C、D三点的坐标；
（2）怎样平移，才能使A点与原点重合？平移后点B、C、D的对应点分别为B₁C₁D₁ ，求四边形OB₁C₁D₁的面积；
（3）平移后在x轴上是否存在点P，使S_△COP=S_四边形OB₁C₁D₁？若存在这样的点P，求出点P的坐标；若不存在，试说明理由．

查看试题解析
22.
如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=3cm，将△ABC沿AB方向向右平移得到△DEF，若AE=8cm，DB=2cm．
（1）求△ABC向右平移的距离AD的长；
（2）求四边形AEFC的周长．

查看试题解析
23.
如图所示的直角坐标系中，三角形ABC的顶点坐标分别是A（0，0）、B（6，0）、C（5，5）．求：
（1）求三角形ABC的面积；
（2）如果将三角形ABC向上平移3个单位长度，得三角形A₁B₁C₁ ，再向右平移2个单位长度，得到三角形A₂B₂C₂ ．分别画出三角形A₁B₁C₁和三角形A₂B₂C₂ ，并试求出A₂、B₂、C₂的坐标．

查看试题解析

（北师大版）2021-2022学年度第二学期八年级数学3.1图形的平移 期末复习测试卷

一、单选题

二、填空题

三、解答题

（北师大版）2021-2022学年度第二学期八年级数学3.1图形的平移期末复习测试卷