(北师大版)2021-2022学年度第二学期八年级数学第二章一元一次不等式和一元一次不等式组 期末复习测试卷
试卷更新日期:2022-06-08 类型:复习试卷
一、单选题
-
1. 下列式子是不等式的为( )A、4 B、x2+x C、4x>7 D、x=32. 下列说法中错误的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则3. 已知a<b , 下列式子不成立的是( )A、a+1<b+1 B、3a<3b C、﹣2a>﹣2b D、如果c<0,那么 <4. 将不等式组的解集表示在数轴上正确的是( )A、
 B、
B、 C、
C、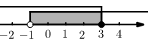 D、
D、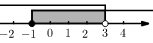 5. 小明将某不等式组的解集在数轴上表示如图所示,则该不等式组的解集为( )
5. 小明将某不等式组的解集在数轴上表示如图所示,则该不等式组的解集为( ) A、x≥2 B、x>2 C、x≥-1 D、-1≤x<26. 已知方程组的x,y满足x﹣y≥0,则m的取值范围是( )A、m≤﹣1 B、m≥﹣1 C、m≤1 D、m≥17. 已知关于 的不等式 的解集为 ,则( )A、 B、 C、 D、8. 如图,直线 与 的交点的横坐标为-2,则关于 的不等式 的整数解为( ).
A、x≥2 B、x>2 C、x≥-1 D、-1≤x<26. 已知方程组的x,y满足x﹣y≥0,则m的取值范围是( )A、m≤﹣1 B、m≥﹣1 C、m≤1 D、m≥17. 已知关于 的不等式 的解集为 ,则( )A、 B、 C、 D、8. 如图,直线 与 的交点的横坐标为-2,则关于 的不等式 的整数解为( ). A、-1 B、-5 C、-4 D、-39. 定义:点A(x,y)为平面直角坐标系内的点,若满足x=y,则把点A叫做“平衡点”.例如:M(1,1),N(-2,-2),都是“平衡点”.当 时,直线 上有“平衡点”,则 的取值范围是( ).A、 B、 C、 D、10. 若数m使关于x的一元一次不等式组 的解集是 ,且使关于y的分式方程 有非负整数解,则符合条件的所有整数m的值之和为( )A、-3 B、0 C、2 D、5
A、-1 B、-5 C、-4 D、-39. 定义:点A(x,y)为平面直角坐标系内的点,若满足x=y,则把点A叫做“平衡点”.例如:M(1,1),N(-2,-2),都是“平衡点”.当 时,直线 上有“平衡点”,则 的取值范围是( ).A、 B、 C、 D、10. 若数m使关于x的一元一次不等式组 的解集是 ,且使关于y的分式方程 有非负整数解,则符合条件的所有整数m的值之和为( )A、-3 B、0 C、2 D、5二、填空题
-
11. 若 , 则 . (填 , 或)12. 关于x的不等式 只有两个正整数解,则a的取值范围是13. 使不等式4x+3<x+6成立的最大整数解是 .14. 如图,直线y=kx+b(k≠0)经过点(﹣1,3),则不等式kx+b≥3的解集为
 15. 如果不等式组 的解集为x<3a+1,则a的取值范围为 .
15. 如果不等式组 的解集为x<3a+1,则a的取值范围为 .三、解答题
-
16. 解不等式组 ,把解集在所给数轴上表示出来,并写出其整数解。
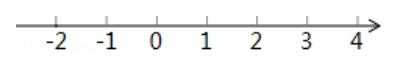 17. 已知不等式组 ,在同一条数轴上表示不等式①,②的解集如图所示,求b﹣a的值.
17. 已知不等式组 ,在同一条数轴上表示不等式①,②的解集如图所示,求b﹣a的值. 18. 某城市平均每天要处理垃圾700吨,有甲、乙两个垃圾处理厂,已知甲厂每小时可处理垃圾55吨,需费用550元;乙厂每小时可处理垃圾45吨,需费用495元,如果规定该城市处理垃圾的费用不多于7370元,甲厂每天至少处理垃圾多少吨?
18. 某城市平均每天要处理垃圾700吨,有甲、乙两个垃圾处理厂,已知甲厂每小时可处理垃圾55吨,需费用550元;乙厂每小时可处理垃圾45吨,需费用495元,如果规定该城市处理垃圾的费用不多于7370元,甲厂每天至少处理垃圾多少吨?
 问x取何值时, >
问x取何值时, >  。
。