江西省九江市湖口县2022年二模数学试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. -3的相反数是( )A、 B、-3 C、3 D、2. 截至2月9日晚21时17分,2022年全国院线电影总票房(含预售)正式突破100亿元大关,用时40天,刷新中国影史年度票房最快破百亿记录,其中电影《长津湖之水门桥》票房已超29.84亿,成为本年度中国影史票房冠军,将29.84亿用科学记数法表示为( )A、 B、 C、 D、3. 如图,几何体的俯视图是( )
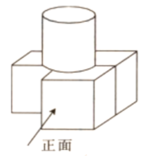 A、
A、 B、
B、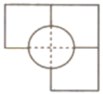 C、
C、 D、
D、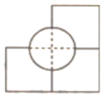 4. 下列计算一定正确的是( )A、 B、 C、 D、5. 如图,∠MON=60°.①以点O为圆心,任意长度为半径画弧,分别交OM、ON于点A,C;②分别以A,C为圆心,OA长为半径画弧,两弧交于点B;③连接AB、BC.若OA=8cm,则四边形OABC的面积为( )
4. 下列计算一定正确的是( )A、 B、 C、 D、5. 如图,∠MON=60°.①以点O为圆心,任意长度为半径画弧,分别交OM、ON于点A,C;②分别以A,C为圆心,OA长为半径画弧,两弧交于点B;③连接AB、BC.若OA=8cm,则四边形OABC的面积为( )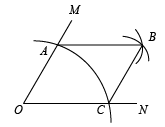 A、 B、 C、 D、6. 已知二次函数的图象只经过三个象限,下列说法正确的是( )A、开口向下 B、顶点在第一象限 C、 D、当时,y的最小值为-1
A、 B、 C、 D、6. 已知二次函数的图象只经过三个象限,下列说法正确的是( )A、开口向下 B、顶点在第一象限 C、 D、当时,y的最小值为-1二、填空题
-
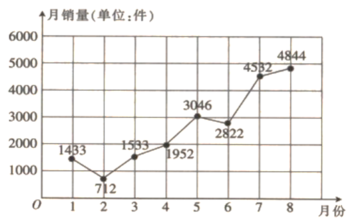
7. 分解因式: .8. 有一组数:1,1,2,3,5,8,13,21,…,称为斐波那契数列,由十三世纪意大利数学家列昂纳多•斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”.该数列从第三项开始,每项等于其前相邻两项之和,则这列数中第九项是 .9. 设是一元二次方程的两个根,则 .10. 防晒衣的主要作用是阻隔太阳紫外线的直接照射,下图为某品牌防晒衣某分店2021年1~8月的销量(单位:件)情况.这8个月销量(单位:件)的中位数是 .
 11. 如图,在中,AD和AE分别是边BC上的中线和高,已知 , 求高 .
11. 如图,在中,AD和AE分别是边BC上的中线和高,已知 , 求高 . 12. 俊俊和霞霞共同合作将一张长为 , 宽为1的矩形纸片进行裁剪(共裁剪三次),裁剪出来的图形刚好是4个等腰三角形(无纸张剩余).霞霞说:“有一个等腰三角形的腰长是1”;俊俊说:“有一个等腰三角形的腰长是”;那么另外两个等腰三角形的腰长可能是 .
12. 俊俊和霞霞共同合作将一张长为 , 宽为1的矩形纸片进行裁剪(共裁剪三次),裁剪出来的图形刚好是4个等腰三角形(无纸张剩余).霞霞说:“有一个等腰三角形的腰长是1”;俊俊说:“有一个等腰三角形的腰长是”;那么另外两个等腰三角形的腰长可能是 .三、解答题
-
13.(1)、计算: .(2)、如图,在中, , BE平分于点D,求证:D是AB中点.
 14. 解不等式组 , 并在数轴上表示他的解集.
14. 解不等式组 , 并在数轴上表示他的解集.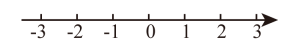 15. 如图,在由边长为1个单位长度的正方形组成的网格中,给出了格点(顶点为网格线的交点),请仅用无刻度直尺按下列要求作图(保留作图痕迹).
15. 如图,在由边长为1个单位长度的正方形组成的网格中,给出了格点(顶点为网格线的交点),请仅用无刻度直尺按下列要求作图(保留作图痕迹). (1)、请在网格①中,作的中位线PQ,交AB于点P,交BC于点Q.(2)、请在网格②中,作矩形ACMN,使16. 2022年印有虎年专属的南昌邮票贴纸进行发售,分别印着“滕王阁”和“绳金塔”图案两种款式,图案形象来源于南昌的两大标志性建筑.旅行社现将1张印有“滕王阁”图案和3张印有“绳金塔”图案的邮票贴纸(邮票贴纸的形状,材料都完全相同)送给四位旅客留作纪念(一人一张).(1)、若游客俊俊从中随机抽取1张,则抽取的邮票贴纸上的图案恰好为“滕王阁”的概率为 .(2)、若游客俊俊先从中随机抽取1张,游客霞霞再从剩余的邮票贴纸中随机抽取1张,请你用列表法或画树状图法表示所有可能情况,并求出两人抽取的邮票贴纸图案恰好一个是“滕王阁”一个是“绳金塔”的概率.17. 图,直线与反比例函数的图象相交于点 , 与轴交于点 .
(1)、请在网格①中,作的中位线PQ,交AB于点P,交BC于点Q.(2)、请在网格②中,作矩形ACMN,使16. 2022年印有虎年专属的南昌邮票贴纸进行发售,分别印着“滕王阁”和“绳金塔”图案两种款式,图案形象来源于南昌的两大标志性建筑.旅行社现将1张印有“滕王阁”图案和3张印有“绳金塔”图案的邮票贴纸(邮票贴纸的形状,材料都完全相同)送给四位旅客留作纪念(一人一张).(1)、若游客俊俊从中随机抽取1张,则抽取的邮票贴纸上的图案恰好为“滕王阁”的概率为 .(2)、若游客俊俊先从中随机抽取1张,游客霞霞再从剩余的邮票贴纸中随机抽取1张,请你用列表法或画树状图法表示所有可能情况,并求出两人抽取的邮票贴纸图案恰好一个是“滕王阁”一个是“绳金塔”的概率.17. 图,直线与反比例函数的图象相交于点 , 与轴交于点 . (1)、求 , , 的值.(2)、是轴上一点,若 , 求点的坐标.18. 随着全国疫情的不断发展,2022年,新冠病毒变异株奥密克戎给人们的生活带来巨大困难,也威胁着人们的生命安全.某校组织了一场关于奥密克戎预防及相关知识讲座,讲座结束后检验学生预防知识的掌握情况,设置了一次满分为“100分”的“奥密克戎”知识问卷,为了了解学生的测评情况,学校在初一、初二两个年级中分别随机抽取了50名学生的分数进行汇总,且分为A,B,C,D,E五个等级(已知分数x均为整数)分别是:
(1)、求 , , 的值.(2)、是轴上一点,若 , 求点的坐标.18. 随着全国疫情的不断发展,2022年,新冠病毒变异株奥密克戎给人们的生活带来巨大困难,也威胁着人们的生命安全.某校组织了一场关于奥密克戎预防及相关知识讲座,讲座结束后检验学生预防知识的掌握情况,设置了一次满分为“100分”的“奥密克戎”知识问卷,为了了解学生的测评情况,学校在初一、初二两个年级中分别随机抽取了50名学生的分数进行汇总,且分为A,B,C,D,E五个等级(已知分数x均为整数)分别是:, 给出如下信息:
①初一年级中,D等级的学生人数占七年级抽取人数的16%.初二年级中,C等级中最低的10个分数分别为70,70,70、72、72,73、73、75、75、75
②两个年级学生奥密克戎预防及相关知识测评分数统计图如下:
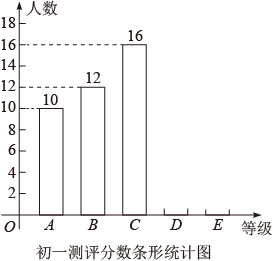

③两个年级学生奥密克戎预防及相关知识测评分数数据如下:
平均数
中位数
众数
初一
79
75
75
初二
76
n
69
(1)、直接写出m、n的值.(2)、补全条形统计图.(3)、若分数不低于70分表示该生对奥密克戎预防及相关知识掌握较好,且该校初一年级有600人,初二年级有500人,请估计该校初一、初二所有学生中,对奥密克戎预防及相关知识掌握较好的总人数.19. 冬奥会期间,各类吉祥物玩偶摆件在市场出现热销,俊俊决定购进“吉祥物毛绒玩具”与“吉祥物金属摆件”两种款式在自家网店销售,已知一件“吉祥物金属摆件”的进价比一件“吉祥物毛绒玩具”多20元,6400元购进的“吉祥物毛绒玩具”数量是4000元购进的“吉祥物金属摆件”的两倍.(1)、每件“吉祥物毛绒玩具”与“吉祥物金属摆件”的进价各多少元?(2)、俊俊通过第一个月的销售数据发现,将“吉祥物毛绒玩具”定价150元销售时,每周可售出10个,销售单价每降价5元,每周销售量可增加1个,若俊俊希望一周销售“吉祥物毛绒玩具”获得720元的销售利润,则“吉祥物毛绒玩具”应如何定价.20. 八一起义纪念碑坐落于江西省南昌市中心八一广场.1977年八一起义五十周年时破土兴建,1979年1月8日落成.如图,为测量八一起义纪念碑的大致高度 , 贝贝在广场平地上的点C处,测得纪念碑的顶部的仰角为30°,贝贝又向纪念碑走近了些测量,于点D处的位置,测得纪念碑的仰角为75°,测得米.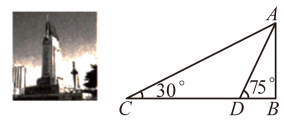 (1)、求贝贝站在D点处仰望纪念碑顶点A的距离AD为多少米?(2)、求八一起义纪念碑的大致高度AB.(参考数据 , 答案精确到0.1米)21. 如图,在中, , AB与相切于点C,延长BO交于点P、Q.连接CP,CQ.
(1)、求贝贝站在D点处仰望纪念碑顶点A的距离AD为多少米?(2)、求八一起义纪念碑的大致高度AB.(参考数据 , 答案精确到0.1米)21. 如图,在中, , AB与相切于点C,延长BO交于点P、Q.连接CP,CQ.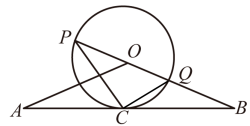 (1)、若 , 求的大小.(2)、若 , 的半径为 . 求边AB的长度.22. 在平面直角坐标系xOy中,若点Q的横坐标和纵坐标互为相反数,则称点Q为“潇洒点”,如点都是“潇洒点”.已知二次函数的图象上有且只有一个“潇洒点” .(1)、小敏认为所有的潇洒点都在同一条直线l上,请直接写出直线l的解析式.(2)、求a,b的值,及二次函数的顶点坐标.(3)、将的图象上移个单位得到抛物线 , 若上有两个“潇洒点”分别是 , 且 , 求当时,中y的最大值和最小值.23. 在矩形ABCD中, , P为CD上的动点.Q为DA上的动点,且 .
(1)、若 , 求的大小.(2)、若 , 的半径为 . 求边AB的长度.22. 在平面直角坐标系xOy中,若点Q的横坐标和纵坐标互为相反数,则称点Q为“潇洒点”,如点都是“潇洒点”.已知二次函数的图象上有且只有一个“潇洒点” .(1)、小敏认为所有的潇洒点都在同一条直线l上,请直接写出直线l的解析式.(2)、求a,b的值,及二次函数的顶点坐标.(3)、将的图象上移个单位得到抛物线 , 若上有两个“潇洒点”分别是 , 且 , 求当时,中y的最大值和最小值.23. 在矩形ABCD中, , P为CD上的动点.Q为DA上的动点,且 . (1)、如图①,当点R在CB上时,求的值.(2)、如图②,PR与CB相交于点N连接QN,当QP平分时,求证: .(3)、在(2)的前提下,连接CR,当时,求的值.
(1)、如图①,当点R在CB上时,求的值.(2)、如图②,PR与CB相交于点N连接QN,当QP平分时,求证: .(3)、在(2)的前提下,连接CR,当时,求的值.